- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
学生在生活中经常遇到圆方面的图形，对本节课会比较有兴趣,并且学过轴对称图形相关知识。同时九年级的同学仍然是比较好奇、好动、好表现的。但在合作交流、探索新知等方面发展的极不均衡。在学习的主动性、积极性等方面也有较大的差异。
自制教具，圆规，三角尺，PPT课件
1、通过观察实验证明,理解掌握垂径定理。
2、会用垂径定理解决有关证明与计算问题。
3、掌握圆中常见辅助线的作法。
【教学难点】
垂径定理的证明和应用。
【教学重点】
运用垂径定理解决有关证明与计算问题
问题教学法、实验教学法、探究教学法、引导发现法
一、预习内容：
自主阅读教材P58-P59
二、预习检测：
1.垂径定理的概念：垂直于弦的直径 这条弦，并且
弦所对的两条弧
2.在下列图形，符合垂径定理的条件吗？
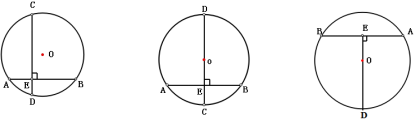
一、情境引入：
1、出示的图片和相关知识简介，提出已知跨度和拱高如何求桥拱所在圆的半径的问题，引入新课。
2、出示本课学习目标。赵州桥
二、探究新知
1、观察和猜想
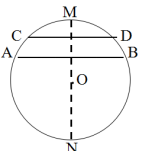
（1）AB、CD是⊙O的两条直径,图1中有哪些相等的线段和相等的弧?
（2）当AB向下平移,如图2变成非直径的弦时,上面的结论还成立吗?
（3）当AB⊥CD时,如图3你认为有相等的线段和相等的弧吗？说说你的猜想。
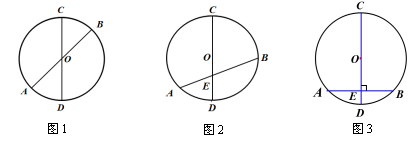
2、证明结论
已知：在⊙O中，CD是直径，AB是弦，CD⊥AB，垂足为E。
求证：AE＝BE，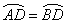
，
。
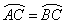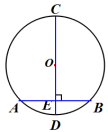
3、归纳定理：
垂径定理：垂直于弦的直径 弦，并且 弦对的两条弧。
几何语言：∵ , ，
∴ ， ， 。
设计意图：培养学生归纳总结能力。
4、理解定理
（1）在下列图形，符合垂径定理的条件吗？
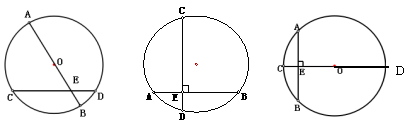
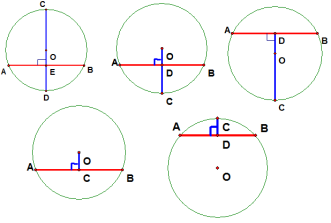
（2）归纳垂径定理的几个基本图形
5、应用定理
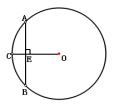
（1）在⊙O中，弦AB垂直于0C，垂足为E，AE=3，则AB= 。
（2）在⊙O中，直径CD垂直于弦AB，垂足为M，AB=12，半径OB=10，则OM= ，CM= 。
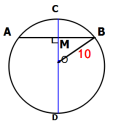
（3）在⊙O中，直径CD垂直于弦AB，垂足为M，CD=20，CM=2，则弦AB=
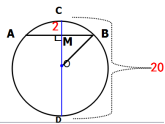
三、巩固提升
例1.如图，弦AB=8cm，CD是直径，CD⊥AB，垂足为E，DE=2cm，求⊙O的直径CD的长。
方法归纳：当半径、半弦、弦心距三个量中不直接具备两个量时，怎么解决？
同步练习：
赵州桥主桥拱的跨度(弦AB的长)为40m,拱高(弧的中点到弦的距离CD的长)为8m，你会求出赵州桥主桥拱的半径吗？
（只列关键算式，不求解）
例2已知：⊙O中弦AB∥CD，求证：弧AC＝弧BD
四、课堂小结
谈谈这节课自己的收获：
1、从知识上我学到了……
２、从方法上我学到了……
五、当堂检测
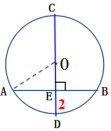
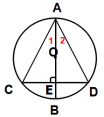
1.如图，如果AB为⊙O的直径，弦CD⊥AB，垂足为E，那么下列结论错误的是（ ）。
A. CE=DE B.弧BC=弧BD
C.∠1=∠2 D.AC>AD
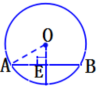
2.半径为2cm的圆中，过半径中点且垂直于这条半径的弦长是 。
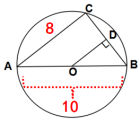
3．AB是⊙O的直径，C是⊙O上一点，AC=8，AB=10，OD⊥BC于点D，求BD的长
六、拓展提升
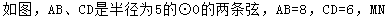
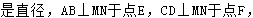
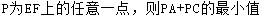
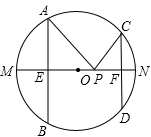
1、如图，OE⊥AB于E，若弦AB=16cm, OE=6cm, 则⊙O的半径是 cm。
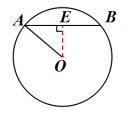
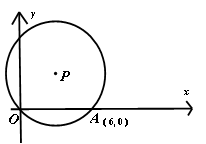
2、如图，在平面直角坐标系中，点O为坐标原点，点P在第一象限，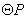
与
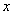轴交于O,A两点，点A的坐标为（6,0），
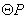的半径为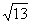
，则点P的坐标为 ____________.
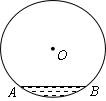
3、一根横截面为圆形的下水管道的直径为1米，管内有少量的污水（如图5），此时的水面宽AB为0.6米．
（1）求此时的水深（即阴影部分的弓形高）；
（2）当水位上升到水面宽为0.8米时，求水面上升的高度．
设为正确答案
湘教智慧云 
贝壳网公众号