- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
本节课时，引导学生从一元一次方程定性解法向多个解的探求过程。引导学生掌握不等式组的解法，区别不等式组和二元一次方程组加减法解题的联系。教学中从学生学习的心理基础和认知特点来说，以感性认识为主，并向理性认知过渡，能逐步熟练地解一元一次不等式组，能将简单的实际问题抽象为数学模型；引导学生认识到数学问题来自于生活，通过实例体会一元一次不等式组是研究量与量之间关系的重要模型之一；生活中处处有数学；有一定的数学转化能力和类比的能力。所以，我对本节课的设计是通过多个学生所熟悉生活情境的问题探求，让学生独立思考，学会合作交流，从而引导其自主学习。基于对本年级各班学生基础的差异分析，我确定了本节课的教学难点是：正确理解并掌握不等式组的解集，掌握文字和图形的数形结合的思想。
本节课的教学工具有三角板，多媒体课件和数码讲台；人民币若干，1.65米的细线和1.70细线。
1.知识技能
（1）学生通过生活实例，了解一元一次不等式组的意义和一元一次不等式组的解集的概念。
（2）掌握一元一次不等式组的解集，掌握不等式的解集和不等式组解集的区别和联系.
（2）会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集.
2.过程与方法
（1）学习一元一次不等式组，掌握一元一次不等式组的解集；经历知识的拓展过程，会应用数轴确定一元一次不等式组的解集,感受并掌握数形结合思想；发展学生的类比推理能力；体会一元一次不等式组是研究量与量之间关系的重要模型之一。
（2）学生通过对一元一次不等式组的学习，能积极参与问题的讨论,；认识到事物间的相依关系。认识生活中存在许多不等的关系式。
3.情感与价值观要求
①参与问题的讨论,体会数形结合思想解决问题的策略,培养自主探索、交流合作的良好习惯.
②认识生活不等内容；培养独立思考，分析问题解决问题的能力；培养学和交流的沟通。
教学重点：
①理解有关不等式组的有关概念.
②会解有两个以及两个以上的一元一次不等式组成的不等式组，并会用数轴确定解集
教学难点：利用数轴确定一元一次不等式组的解集；通过实例体会一元一次不等式组是研究量与量之间关系的重要模型之一。
教学方法：探求与合作交流，类比推理法;预设的教学方法；启迪和推理，类比与联想。
教具：多媒体和三角板
教学内容及过程：
一、回顾与提问
1．什么叫一元一次不等式?它的解集和解有什么区别。
2．解一元一次不等式的步骤是什么?
二、（1）创设情境、导入新课
生活中存在许多不等的事例，本章节从学习一元一次不等式入手，从二元一次方程和二元一次方程组的联系推断一次不等式和一元一次不等式组之间的关联。他们的解法和二元一次方程组的解法相同吗？请同学们通过下面两个例子讨论和交流后发表自己的见解.
例1.学校要进行第二十一届运动会，挑选一些学生作为志愿者加强运动场的安全措施；
分析：①志愿者的身高不小于1650cm
②志愿者的身高不超过170cm
你能用你所学的知识来判断学校挑选的志愿者的身高的范围吗？
小组交流：
① 所谓“志愿者身高”，设身高为xcm;x的值不是唯一的，
满足①x≥165cm和②x≤170cm；可以确定志愿者的身高范围值在165cm-170cm之间.
②类比：二元一次方程组是由两个二元一次方程组成的；
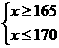联想：
那么一元一次不等式组也是由两个不等式组成的，即
例2.某商店一种商品原价是每件10元，六一儿童节来临之际，商店推出这种商品的让利游戏转盘，圆盘面分为相等的四份，圆面上分别标有数字“九折”，“八折”，“七折”和“六折”，转动转盘一下，指针落在所在的区域就打几折;小明欲购买这种商品；转动转盘一下，则购买这种商品的价格的范围是多少？
分析：①商品的原价是10元，打折销售的方式有四种，分别对应的价格是9元，8元，7元，6元。
②随机转动转盘，购买商品的价格是9元，8元，7元，6元中的一种。所以购买这种商品的价格的范围是6元到9元之间。
小结：
上述生活中的不相等实例，可以转化为数学建模中不相等的实例；通过建模转化为数学上不等的的思想；引导学生学习和老师之间的交流。
(2)新课讲授
(1)课前预习
问题：用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水，估计积存的污水在1200 吨到1500吨之间，那么大约需要多少时间才能将污水抽完?
分析: 要解决上述问题,假设抽水机需要x分钟才能将污水抽完;
探索出这个实际问题中包含着两个应该同时满足的两个条件。
①第一个要满足的条件是总抽水量30x吨应大于1200吨，
②第二个要满足的条件是总抽水量30x吨应小于1500吨，
(2)概念的引入
①一元一次不等式组的有关概念
几个一元一次不等式合在一起就组成了一个一元一次不等式组，
重点：本节重点研究两个一元一次不等式组成的不等式组。
②不等式组和不等式组的解集
(1) 一元一次不等式组的解集:几个一元一次不等式的解集的公共部分.
(2)求不等式的解集的过程，叫做解不等式组。
(3)解一元一次不等式组的步骤：
①求出这个不等式组中每个不等式的解集；
②借助数轴求出这些不等式的解集的公共部分。
(3)例题的讲解
解下列不等式组
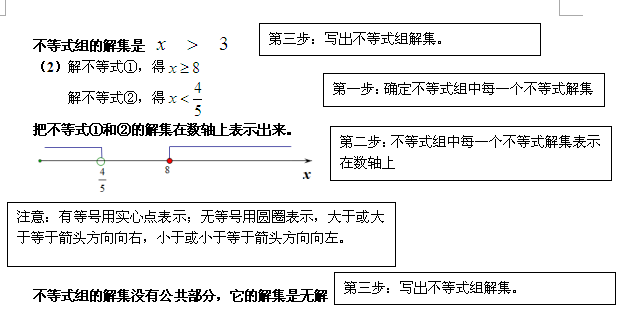
小结归纳：
（1）一般地，关于同一个未知数的几个一元一次不等式合在一起，就组成了一个一元一次不等式组；不等式组是几个不等式的组合，所以x的值应是每个不等式的解集的组合.即每个不等式的解集相同的部分。
：
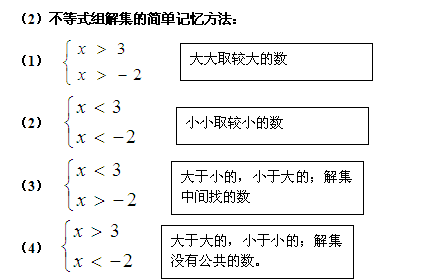
五、课堂练习
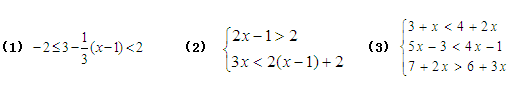随堂练习：教材P129页练习：1,2 ； 补充练习：解不等式组
六、课时小结
本节课学习了如下内容：
1.理解有关不等式组的有关概念;学习一元一次不等式组是数学知识拓展的需要，也是现实生活的需要，不等式组的知识源于生活实际，要学会分析现实世界中量与量的不等关系，解一元一次不等式组。
2.会解有两个一元一次不等式组成的一元一次不等式组，并会用数轴确定解集.一元一次不等式组的解集在数轴上表示可以加深对一元一次不等式组解集的理解，也便于直观地得到一元一次不等式组的解集，体现了数形结合的数学思想方法。
七：作业布置：
教材P129页复习巩固：1（1）（3）
2（2)（4）
七：板书设计
教学后记：
设为正确答案
湘教智慧云 
贝壳网公众号