- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



八年级的学生在学习了数轴的概念后,已经有了一定的数形结合的意识,积累了一定的由数轴坐标描出数轴上点及由数轴上的点写出数轴上坐标的经验。而如何从一维数轴点与实数之间的对应关系过渡到二维坐标平面中的点与有序数对之间关系,限于初中的学习范围与学生的接受能力,学生理解起来有一定的困难,同时本节内容中概念较多,比较琐碎,如何熟练运用对学生来说也有一定困难。因此,教学过程中创设生动活泼、直观形象、且贴近他们生活的问题情境,会引起学生的极大关注,会有利于学生对内容的较深层次的理解;另一方面,学生已经具备了一定的学习能力,可多为学生创造自主学习、合作交流的机会,促使他们主动参与、积极探究。
直角三角板、坐标纸、多媒体课件
知识与技能:
1、理解有序数对的意义;
2、能用有序数对表示实际生活中物体的位置;
3、理解平面直角坐标系的相关概念;
4、在给定的平面直角坐标系中,会由点的位置写出点的坐标,由点的坐标确定点的位置;
5、理解每个象限及坐标轴上的点的特征。
过程与方法:
学生经历有序数对的学习过程,培养学生的概括能力,发展学生的数感,体会具体-抽象-具体的数学学习过程经历坐标概念的形成,培养学生的观察归纳能力,领会数形结合的思想。
情感态度与价值观:
通过在游戏中学习有序数对,培养学生合作交流意识和探索精神,经历用有序数对表示位置的过程,体验数、符号是描述现实世界的重要手段。
重点:有序数对及平面内确定点的坐标、平面直角坐标系及相关概念
难点:利用有序数对表示平面内的点,根据点的位置写出点的坐标
以多媒体课件创设情景,在教师的指导下,引导学生从已有的知识和经验出发,观察思考,自主学习,交流合作,归纳发现,探索新知,让学生参与知识形成的全过程。
学生活动1:找
找一找,在相片中你能找出老师学生时代的像吗?

1、同学们,这是老师珍藏30多年的相片------- 读小学的合影照,你们能在这张相片中找到我吗?(教师利用这个话题对学生进行思想教 育)
2、 老师在第一排,左边第五个,这时你找到了吗?
比一比,看谁反应快!
以教室最左边的小组为第一组,依次为第二组、三组、....靠近讲台的为第一排,依次为第二排、三排、...请同学们记住自己的位置,老师说到“几组几排”的同学要马上站起来,老师点到名的同学要立刻能说出自己是“几组几排”。
通过学生活动1、2 引出有序实数对和新课
1、学习平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分。


(画一画,看谁的平面直角坐标系画得更规范)
如图,你如何确定点P 坐标呢?
 →
→ 
如图:为了用有序实数对表示点P,过点P 作x轴的垂线,垂足点表示a,再过点P 作y轴的垂线,垂足点表示b,则点P的坐标为(a,b)。
强调★ 表示点的坐标:横坐标在前,纵坐标在后,中间隔开用逗号,一定要加括号。
例如:在下列平面直角坐标系中,A点坐标为 ,B点坐标为 。

学生活动4:看
看一看,你能写出图中各点的坐标吗?(口答)


(1)、由此可见,平面直角坐标系中的任何一点都可以用一对有序实数对来表示。
(2)、你能说出各象限内的点及坐标轴上的点的特征吗?
由师生共同归纳得:
1、各个象限内的点的坐标特征是:
第一象限(+,+),即(x>0,y>0) 第二象限(-,+),即(x<0,y>0)
第三象限(-,-),即(x<0,y<0) 第四象限(+,-)。即(x>0,y<0)
2、坐标轴上的点的坐标特征是:
坐标轴上的点的坐标中至少又一个是0;
横轴上的点的纵坐标为0,即(x,0)
纵轴上的点的横坐标为0,即(0,y).
已知点Q的坐标为(m,n),如何确定Q的位置呢?
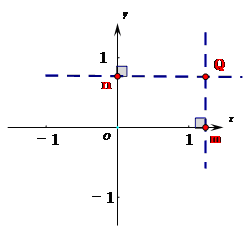
如图: 1、过在x轴上表示m的点作x轴的垂
2、过y轴上表示n的点作y轴的垂线
3、两线的交点即为点Q。
做一做,在直角坐标系中,描出下列各点:A(4,3)、B(-2.5,3.5)、C(-4,-1)、D(2,-2)、E(0,2)、F(3,0).
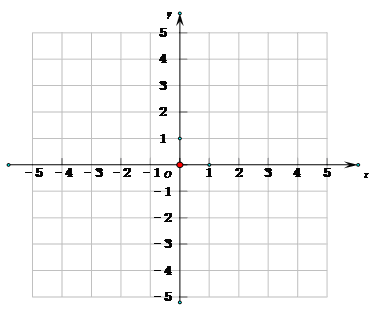
由此可见,任何一对有序实数对都可以在平面直角坐标系中的表示出来。
综上所述:平面上的点与有序实数对一 一对应。
练一练,完成下列各题
1、点(3,-2)在第 象限,点(0,3)在 轴上。
2、在平面直角坐标系内,下列各点在第二象限的是( )
A(2,1) B(-2,1) C(-3,-5) D(3,-5)
3、已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
学生活动7:议
议一议,你能给你的组员一个惊喜吗?
1、(2016年汕头中考)已知点P(m+2,m-1)在x轴上,则点Q(2m-7,1+m)在第 象限.
2、(2016年岳阳中考)已知点P(3-a,a-7)在第三象限,则a的取值范围是 。
四、课堂小结
本节课你有哪些收获?
1、知道平面直角坐标系上的点与有序实数对是一一对应的。
2、认识并能画出平面直角坐标系。
3、在给定的直角坐标系中,由点的位置写出它的坐标;由点的坐标确定点的位置。
4、各个象限内的点的坐标特征是:第一象限(+,+), 第二象限(-,+),
第三象限(-,-), 第四象限(+,-)。
5、坐标轴上的点的坐标特征是:坐标轴上的点的坐标中至少又一个是0;
横轴上的点的纵坐标为0,即(x,0)
纵轴上的点的横坐标为0,即(0,y)
五、课后作业 书P86 练习1、2
预习教材P86—88并完成课后练习。
设为正确答案