- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



学生在七年级对数据的收集和整理已有所了解,已具备了从“表格”中获取相关信息的能力。同时,学生的“数形结合思想”、“建模思想”已初步形成,为开展本次教学活动打下了一定的基础。
多媒体教学、卷尺
知识与能力目标:初步学会从数学的角度出发提出问题,理解问题,并能综合运用所学知识和技能解决问题,形成如何决策的具体方案。
过程与方法目标:体会“数形结合”、“数学建模”思想在数学应用中的重要地位。
情感态度与价值观:在数学学习活动中获得成功的体验,建立自信心,通过视频短片培养学生主义情怀。
会从不同信息中利用待定系数法求一次函数的表达式
情境导入法
一、情景导入,生成问题
说一说
1、你们喜欢体育运动吗?
2、你们了解撑杆跳高吗?


(教学说明:通过2016年里约奥运会的男子撑杆跳高中国选手决赛的视频导入,激发学生对本堂课的学习欲望和激情)
二、合作交流,探究新知
动脑筋:
国际奥林匹克运动会早期,撑竿跳的记录近似地由下表给出:
年份 | 1900 | 1904 | 1908 |
高度(米) | 3.33 | 3.53 | 3.73 |
观察这个表格中第二行的数据,可以为奥运会的撑杆跳高记录与时间的关系建立函数模型吗?
分析:上表中每一届比上一届的记录提高了0.2米,可以试着建立一次函数的模型。
用t表示从1900年开始的年份,则在奥运会早期,撑杆跳高的记录y(米)与t的函数关系式为 y = kt + b
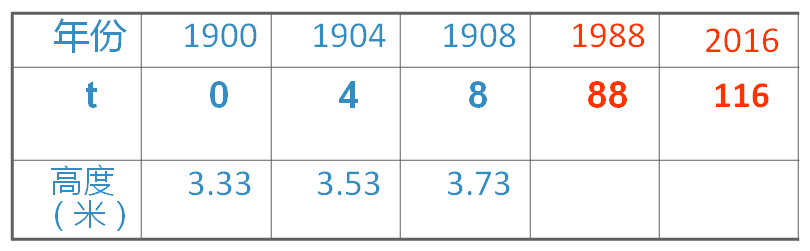
年份 | 1900 | 1904 | 1908 |
t | 0 | 4 | 8 |
高度(米) | 3.33 | 3.53 | 3.73 |
由于t=0(即1900年)时,长杆调高的记录为3.33米,t=4(即1904年)时,记录为3.53米,因此
解得 k=0.05
所以奥运会早期撑杆跳高记录y与时间t的函数关系式为:
y=0.05t+3.33 (*)
做一做:你能利用公式(*)预测1912年和1916年奥运会的男子撑杆跳高记录吗?
解:当t=12时(表示1912年),y=0.05×12+3.33=3.93
当t=16时(表示1916年),y=0.05×16+3.33=4.13
想一想:能用这个模型(*)预测1988年的奥运会男子撑杆跳高记录吗?
解:当t=88时(表示1988年),y=0.05×88+3.33=7.73
而1988年奥运会的男子撑杆跳高实际记录为5.90米。
思考:从此你们可以得出什么结论吗?
(结论:根据1912年和1916年的预测数据和实际数据。这说明用所建立的函数模型,在已知数据邻近做预测,是与实际事实比较吻合的。
根据1988年的预测数据和实际数据。这表明用所建立的函数模型远离已知数据做预测是不可靠的。)
三、典例精析,能力生成
快来游戏:
(设计游戏:请两组同学(一组为两名高矮不一样的男同学、一组为两名高矮不一样的女同学)上台伸出手掌,比较他(她)们的“指距”)
问:同学们,请观察他们的“指距”,你们发现了什么吗?
(讲解完例题后,回到这个问题上,再从学生中随机抽取两名学生(一男一女),测量他们的指距和身高,验证我们所求的一次函数的实效性)
例1 请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离为指距。已知指距与身高具有如下关系:
指距(cm) | 19 | 20 | 21 |
身高(cm) | 151 | 160 | 169 |
(1)求身高y与指距x之间的函数表达式;
(2)当李华的指距为22cm时,你能预测他的身高吗?
解:(1)上表2组数据反映了身高y与指距x之间的函数关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型。
设身高y与指距k之间的函数关系表达式为y=kx+b,
将x=19,y=151与x=20,y=160代入上式, 得:
解得:k=9,b=-20
于是身高y与指距k之间的函数关系表达式为y=9x-20
(2)当x=22时,y=9 × 22-20=178. 因此,李华的身高大约是178cm.
四、随堂训练,巩固提高
小明在练习100米短跑,今年1月至4月份的100米短跑成绩如表所示:
月份 | 1 | 2 | 3 | 4 |
成绩(秒) | 15.6 | 15.4 | 15.2 | 15.0 |
(1)你能为小明的100米短跑成绩与时间的关系建立函数关系模型吗?
(2)用所求出的函数解析式预测小明今年6月份的100米短跑成绩。
(3)能用所求出的解析式预测小明明年12月份的100米短跑成绩吗?
五、归纳总结,能力升华
同学们,通过这节课的学习,你们知道一次函数的应用一般步骤是什么了吗?
六、课后作业
P137 练习第1题、第2题
设为正确答案