- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《三角形》是湘教版八年级数学上第二章《三角形》的第一节的内容。三角形是最常见最基础的几何图形之一,是初中平面几何学习的真正开始。学生在小学学段已学过三角形的一些知识,对三角形的许多性质有所了解,在七年级又学过点,线,角等知识、会进行简单的说理,都对本节课的学习打下了坚实的基础。由于八年级学生的抽象思维还不够成熟,因此教学时要以实际情景引出问题,使学生初步经历在具体情景中提出问题和解决问题 的过程,获得学数学,用数学的乐趣,让学生感知数学来源于生活,又服务于生活。此阶段的学生应用数学知识解决实际问题的能力还不强,因此教学时适当设计一些练习,加强学生运用数学的能力。
八年级数学是初中数学的重中之重,对学生智力的开发和思维的发展是至关重要的。下面对我班的数学学习现状做一下简单的描述。
一、学习状态
大部分同学都能跟上进度,其中有些学生表现还比较出色,但有一小部分同学的理解能力和接受能力较差而且学习习惯不好所以成绩不理想。还的几个上课注意力不集中很容易分心,作业和试卷上的错误比较多,对老师的提问一问三不知,在今后的教学过程中对这些孩子要特别注意。
二、学习习惯
部分学生学习习惯较好,热情很高,能主动按时完成 学习任务。但还有一部分学生学习习惯差,上课听讲不专心,不主动思考问题或尝试解决问题依赖老师和同学帮助。抄作业现象比较严重。
三、解决方案及实施计划
1、兴趣是最好的老师,激发学生学习兴趣,帮助学生养成良好的学习习惯。改正抄作业的现象。
2、重视学生主动学习能力的培养,进一步加强学生运算能力和思维能力的培养。
3、对优生致力于发展性思维训练。让学生进一步掌握学习策略。
4、注重正确价值观的培养让学生了解数学知识的形成过程和应用价值,发挥评价的激励和导向功能,帮助学生认识自我、建立自信。
知识与能力:
1、使学生理解三角形的概念,能用符号语言表示三角形。
2 、了解三角形的分类,特别是等腰三角形与等边三角形的区别与联系。
3、探索三角形三边的关系,能运用三角形三边的关系解决问题的能力。
方法与过程:
通过提问引导,合作探究的教学培养学生分析问题、解决问题的能力。
情感、态度与价值观:
渗透分类讨论的数学思想,把实际问题转化为数学问题,促进数学思维的发展;培养学生良好的学习习惯。
重点:三角形的有关概念和符号表示方法,三角形的分类以及三角形三边的关系。
难点:三角形三边关系及运用。
2.1三角形(第一课时)
定义:不在同一直线上的三条线段首尾相接所构成的图形。
三角形的表示:
三角形的顶点,内角,边
三角形的分类:按角分 按边分
三边关系:任意两边之和大于第三边。
任意两边之差小于第三边。






多媒体展示图片
看一看找出图中的三角形,并把它们勾画出来,你还能举出一些其它的实例吗?
想一想:1、什么样的图形是三角形?
三条线段组成的图形一定是三角形吗?画一画,想一想,拼一拼。
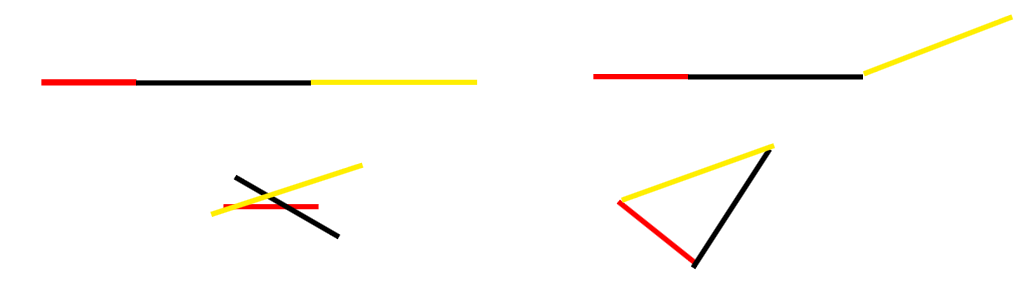
分组操作讨论,学生总结归纳得出结论:
不在同一直线上的三条线段首尾相接所构成的图形叫作三角形。
注意点:1、三条线段
2、不在同一直线上
3、首尾相接
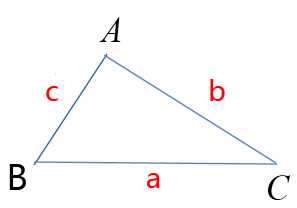
1、如何用符号语言来表示一个三角形?
三角形ABC 记作:
2、你能找出三角形ABC的顶点,内角,边吗?
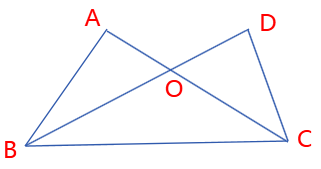
(1)如图,图中有几个三角形?把它们分别表示出来。
(2)如图在三角形DBC中写出角D的对边,BD边的对角。
3、想一想:生活中的三角形是怎么分类的呢?
学生观看微课学习三角形的分类。
你会把下面的三角形分类了吗?
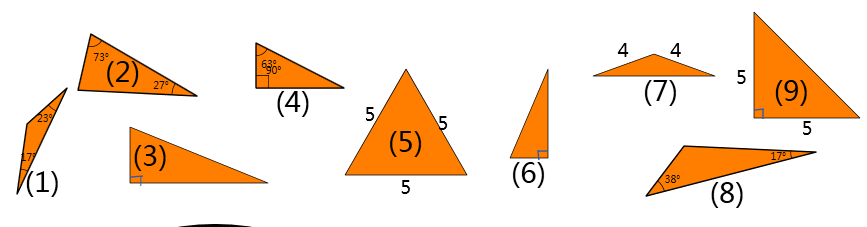
(1)按角分:锐角三角形,钝角三角形,直角三形
(2)按边分:
不等边三角形——三边都不相等的三角形。
等腰三角形——有两条边相等的三角形。

说明:等边三角形(正三角形)是特殊的等腰三角形是腰和底边相等的等腰三角形。
引导学生认识等腰三角形的顶角,底角,腰,底边。
1、对子互学:
一只小蚂蚁想从B地去C地,它有两条路可以选择一条是从B地爬到C,另一条是从B地爬到A地再到C地。两条路线的路程一样吗?为什么?
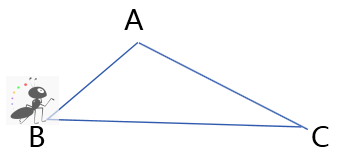
学生之间讨论得出答案,BC<AB+AC. 理由:两点之间线段最短。
学生总结:三角形任意两边之和大于第三边。
验证与推理:画一画,量一量,算一算:
小组活动:
第一步:每个同学在纸上画一个任意的三角形,分别量出三角形三条边的长度。
第三步:验证两边之和与第三边的关系。
总结:三角形任意两边之和大于第三边。
想一想:有三根木棒,其长度分别为2cm,3cm ,6cm它们能否首尾相接构成一个三角形?
四、展示提升:
展示一:三角形任意两边之差与第三边的长度之间的大小有何关系?
画一画,量一量,算一算
分组活动:每个同学在纸上画一个任意的三角形,分别量出三角形的三条边的长度,算一算你们发现了什么?小组人员通过分析数据得出结论。
小组长展示探究结果:
三角形任意两边之差小于第三边。
展示二:
下列长度的三根木棒能构成三角形吗?为什么?
(1)3cm,5cm,10cm (2)5cm,4cm,8cm
总结方法:
挑战自我,相信自己一定行,设计一个竞赛游戏,让两们同学上台比拼!
下列长度的线段能组成三角形的是:
4,7,8 4,2,7 4,5,6 3,4,5 2,2,4 22,23,24 8,8,15 1,7,9 6,6,1 34,23,58
试一试:
例1、如图,D是ABC的边上一点,AD=BD,试判断AC与BC的大小.
解 在ABC中, 有BD+DC>BC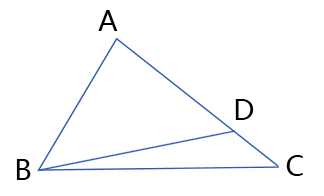
又 AD=BD
BD+DC=AD+DC=AC,
所以AC>BC
通过这节课你学到了哪些知识?

1、已知三角形三边长分别为2,x,13若x为正整数,则这样的三角形个数有( )个。
2、人四根长度分别是12cm,10cm,8cm,4cm的木头,选其中3根组成三角形,能组成三角形的个数有( )个。
3、一个等腰三角形有两边长为2和5,则它的周长是( ),若它的边长是3和5,那么它的周长是( )。
4、一个三角形的两边分别是7和2,且它的周长为奇数,则第三边长是( )。
设为正确答案