- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
本节课是高中数学人教A版必修5第一章第二节的内容，是在学生学习上一节正弦定理、余弦定理的基础上，运用这两个定理解决实际问题，并说明这两个定理在解决测量、工业、几何等方面的实际问题，使学生掌握解任意三角形的知识在实际中有广泛的应用，提高运用所学知识解决实际问题的能力。
本章开头提出：在我国古代就有嫦城奔月的神话故事.明月高悬，我们仰望夜空，会有无限遐想，不禁会问，遥不可及的月亮离地球究竟有多远呢?
早在1671年、两个法国天文学家就测出了地球与月球之间的距离大约为385400km，他们是怎样测出两者之间距离的呢?
在数学发展历史上，受到天文测量、航海测量和地理量等方面实践活动的推动、解三角形的理论得到不断发展并被用于解决许多测量问题。
在初中，我们已经能够借助于锐角三角函数解决有关直角三角形的一些量问题，在实际工作中我们还会遇到许多其他的测量问题，这些问题仅用锐角三角函数就不够了如：
1.怎样在航行途中测出海上两个鸟屿之间的距离?
2.怎样测量底部不可到达的建筑物的高度?
3.怎样在水平飞行的飞机上测量飞机下方山顶的海高度?
4.怎样测出海上航行的轮船的航速和航向?
这些问题的解决需要我们进一步学习应用这两个定理解三角形以及解决实际测量中的一些问题.同时说明了这两个定理的应用非常重要，由此可见实际测量在本章的中心地位。
学生在初中已经学习过解直角三角形，能够通过建立直角三角形模型解决实际问题中的长度和角度的测量，在必修一中学生已经学习过数学建模的知识，了解建模的基本过程。在本章第一节学生学习了正弦定理和余弦定理，这些知识都将为本节课的学习奠定基础，在此基础上进一步向探究构建多个三角形的问题自然过渡。
在研究中，学生无法构建数学模型，或者是没有从所给的背景资料中正确地提取出数学信息也将成为本节课学习的障碍，在完成测量任务的过程中依靠实际生活背景，指导学生运用简单的测量工具，帮助学生理解有关数学概念，借助课本例题引导学生应用于实际问题，坚持引导——讨论——归纳，目的不在于让学生记住结论，更多地要养成良好的研究、探索习惯。
1.能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题；
2.激发学生学习兴趣、体会数学的应用价值、培养学生运用图形、数学符号表达题意和应用转化思想解决数学问题的能力.
3.在利用正弦定理、余弦定理解决一些实际问题的过程中，逐步培养学生实事求是、扎实严谨的科学态度、爱国主义精神，学会用数学思维方式去解决问题和认识世界.
重点：
能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题.
难点：
1.理解题意，设计方案进行测量，把实际问题转化为数学模型进行计算；
2.理解有关角的概念，应用空间想象能力，把有关距离问题转化为数学模型进行计算。
课题：正余弦定理应用举例 类型一 探究1 【变式】 | 类型二 探究2 【变式】 | 类型三 探究3 【变式】 | 作业安排 |
板书说明：有些板书可以用展示台代替。
1.回忆正弦定理余弦定理：
在ΔABC中，角A、B、C的对边为a、b、c，
（1）正弦定理：
(R为ΔABC外接圆的半径).
（2）余弦定理：
,
, 
2.提问：
正、余弦定理的数学表示及正、余弦定理能解决的三角形问题的类型（据学生的回答师生共同评价、补充）
正弦定理主要解决已知两角和一边解三角形，已知两边和其中一边的对角解三角形.
余弦定理主要是以下两类有关三角形的问题：
(1)已知三边，求三个角.这类同题由于三边确定.
(2)已知两边和它们的夹角.
今天我们开始学习正余弦定理在科学实践中的重要应用——距离的测量.
温馨提示：常用测量工具有经纬仪（测角）和钢卷尺（测距离）
类型一 ： 两点间可视但不可达距离的测量
探究1：在不可到达的情况下，如何测量海边某炮军基地A与钓鱼岛C这两地之间的距离。
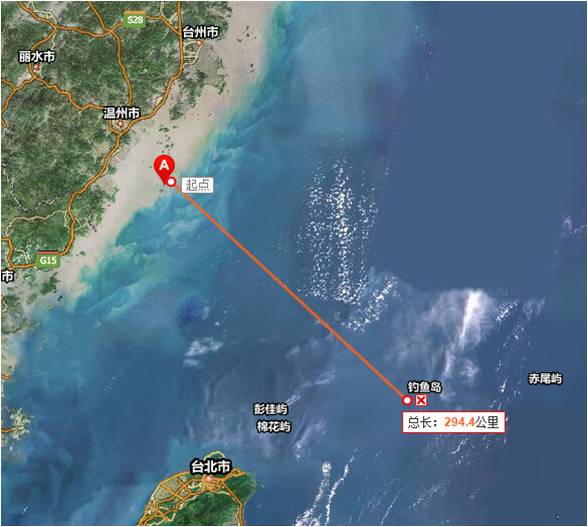
先看PPT引导的视频：中日钓鱼岛之战——砺剑钓鱼岛
看完视频，强调中国人民寸不让。
提问：
1、基线:在测量时，根据测量需要适当确定的线叫基线.
2、在解三角形时，已知两角一边，可用正弦定理求其中另两点之间的距离.
分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,仪器测出AB基线长、
、
的大小，相当于已知两角一边，可用正弦定理来求解AC。
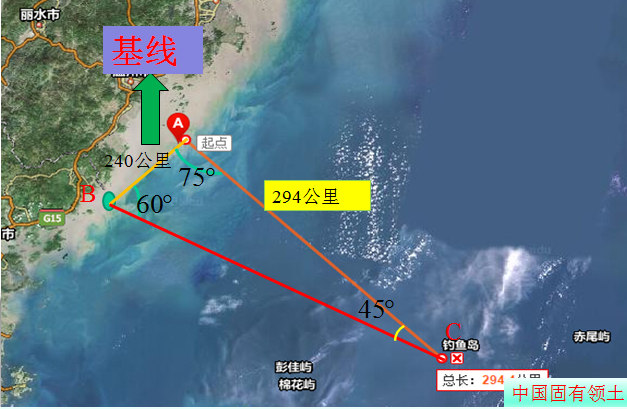
略解：ΔBC中
.
【变式】如图，为测量河的宽度，在一岸边选定两点A，B，望对岸的标记物C，测得∠CAB=45o,∠CBA=75o,AB=120m，求河宽CD。
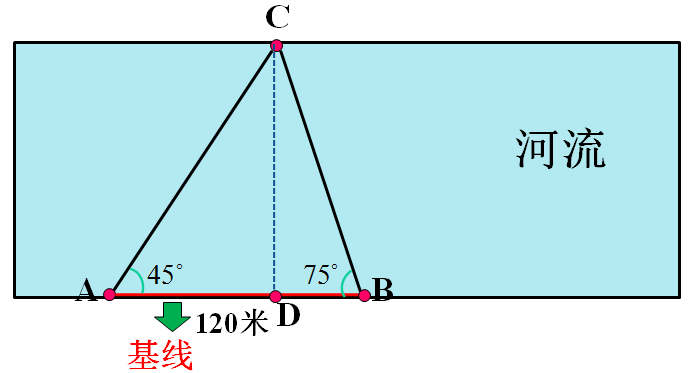
略解：在ΔBC中，
，
在ΔCD中，利用正弦定理得
类型二： 两点间不可视也不可达距离的测量
探究2：如下左图，为了测量钓鱼岛两侧舰艇A，B之间的距离,给定下列四组数据，测量时应当测的数据是（ ）
A.α,a,b B.α,β,γ C.a,b,γ D.β,a,b
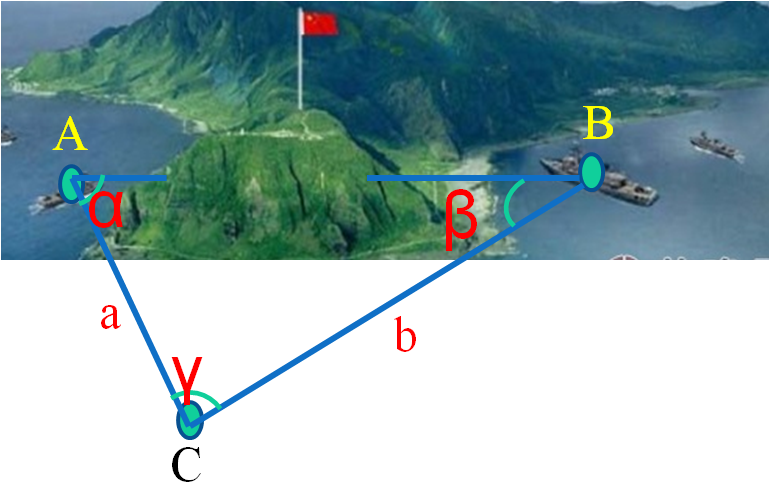
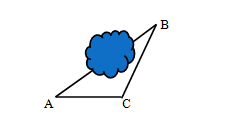
略解：相当于已知两边及其夹角，可用余弦定理解得，故选C。
总结：在解三角形时，已知两边与夹角，可用余弦定理求另一边的长度.
【变式】（湖南学考）如上右图，在高速公路建设中需要确定隧道的长度，工程技术人员已测得隧道两端的两点A，B到点C的距离AC=BC=1km，且C=120o，则A，B两点间的距离为 （ ）
A. 
km B.
km C. 1.5km D.2km
略解：利用余弦定理得
,选A。
类型三：C，D与点A，B均可视但不可达
探究3：在某次军事演习中，红方为了准确分析战场形势，在两个相距1000m的军事基地C和D处，测得蓝方两支精锐部队分别在A、B处,∠ADB=30o,∠BDC=30o,∠DCA=60o，∠ACB=45o,求蓝方这两支精锐部队的距离。
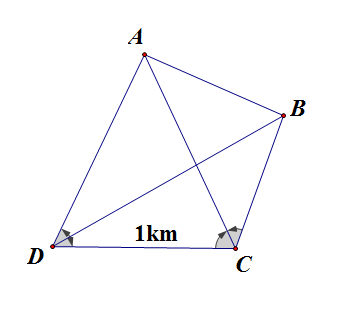略解：由边角关系可知ΔACD为正三角形，得AB=1km,
在ΔBCD中，由正弦定理得
.
在ΔABC中，由余弦定理得
分析：需求AB的长度，ΔACD中，利用边角关系求AC，在ΔBCD中，利用正弦定理求BC，在ΔABC中，利用余弦定理求AB。
解题步骤总结：
（1）分析题意，画出图形，明确已知与所求
（2）选定或创建三角形，注意利用基线
（3）确定用正弦定理还是用余弦定理
【变式】（2014高考）如图所示，我炮兵阵地位于地面A处，两观察所分别位于地面点C和D处，已知CD=6000m,∠ACD=45o,∠ADC=75o,目标出现于地面B处时，测得∠BCD=30o,∠BDC=15o,炮兵阵地到目标的距离是 （结果保留根号）。
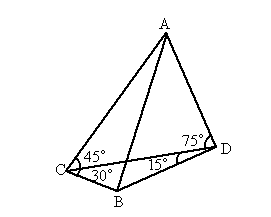
求距离类型总结
| 类别（测A、B两地距离） | 图示 | 测量 | 方法 |
| A、B两点可视但不能到达 | 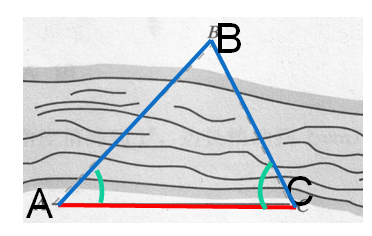 | ∠A、∠C、AC | 利用两角一边，求AB，正弦定理 |
| A、B两点不可视也不能到达 | | AC、BC、∠C | 利用两边夹其夹角，求AB，余弦定理 |
| A、B两点都不能到达 | 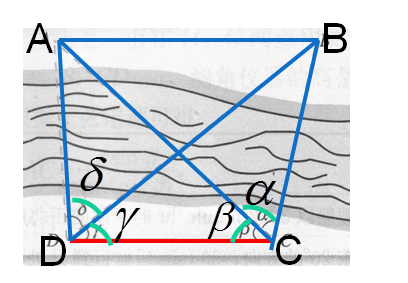 |  、 、 、 和CD | ΔACD中，利用边角关系求AC，在ΔBCD中，利用正弦定理求BC，在ΔABC中，利用余弦定理求AB |
导学案课后作业1，2
设为正确答案
湘教智慧云 
贝壳网公众号