- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节内容是普通高中教科书人教A版第二册《统计》部分第九章《9.2.2总体百分位数的估计》的内容。统计是一门应用性很强的学科。它的概念和方法产生的动力来自于解决实际问题的需要。结合具体案例,由问题来驱动统计概念和方法学习,不仅符合统计学科的特点,而且可以克服概念和方法的抽象带来的理解困难。本节课探究栏目提出“居民生活用水定额管理问题”,在制定水价问题中提出总体百分位数的概念,让学生尝试运用总体百分位数的估计来解决实际问题,体会总体百分位数的估计的意义与作用,体会用样本估计总体的思想与方法。发展学生数据分析、数学运算、数学建模的核心素养。
在学习本节内容之前,学生对统计的相关概念、统计图表及用样本数据的频率分布估计总体分布已经有了一定基础,能够运用所学知识解决一些统计问题,但实际问题中对数据的分析仅仅靠已有的知识还完全不够,所以还需要依据实际问题的需要学习更多的统计知识。
本节课通过对百分位数的学习,培养学生数学抽象的能力、数学运算的能力以及数据分析、探索新知的能力,在教学过程中渗透类比、归纳的数学思想。在掌握统计原理的同时,将课堂延伸到课程以外,合理使用信息技术,将学生从机械繁琐的数据处理中解放出来,把更多的精力集中放在对概念方法的理解上。
1.结合实例,体会百分位数的意义;
2.理解百分位数的统计含义并会就具体数据求得总体的百分位数的估计值,掌握求第P百分位数的步骤;
3.通过对百分位数的学习,培养学生数据分析素养、数学运算和数学建模素养。
4.培养学生分析问题、探索新知的能力,渗透类比、归纳数学思想。
5.让学生感受数学对实际生活的需要,认识到数学知识源于生活并指导生活的事实,体会数学知识与现实世界的联系。
教学重点:理解百分位数的概念,掌握其简单应用;理解百分位数在统计学中的作用和意义。
教学难点:掌握求一组数据的第p百分位数的步骤;体会样本百分位数估计总体的过程。
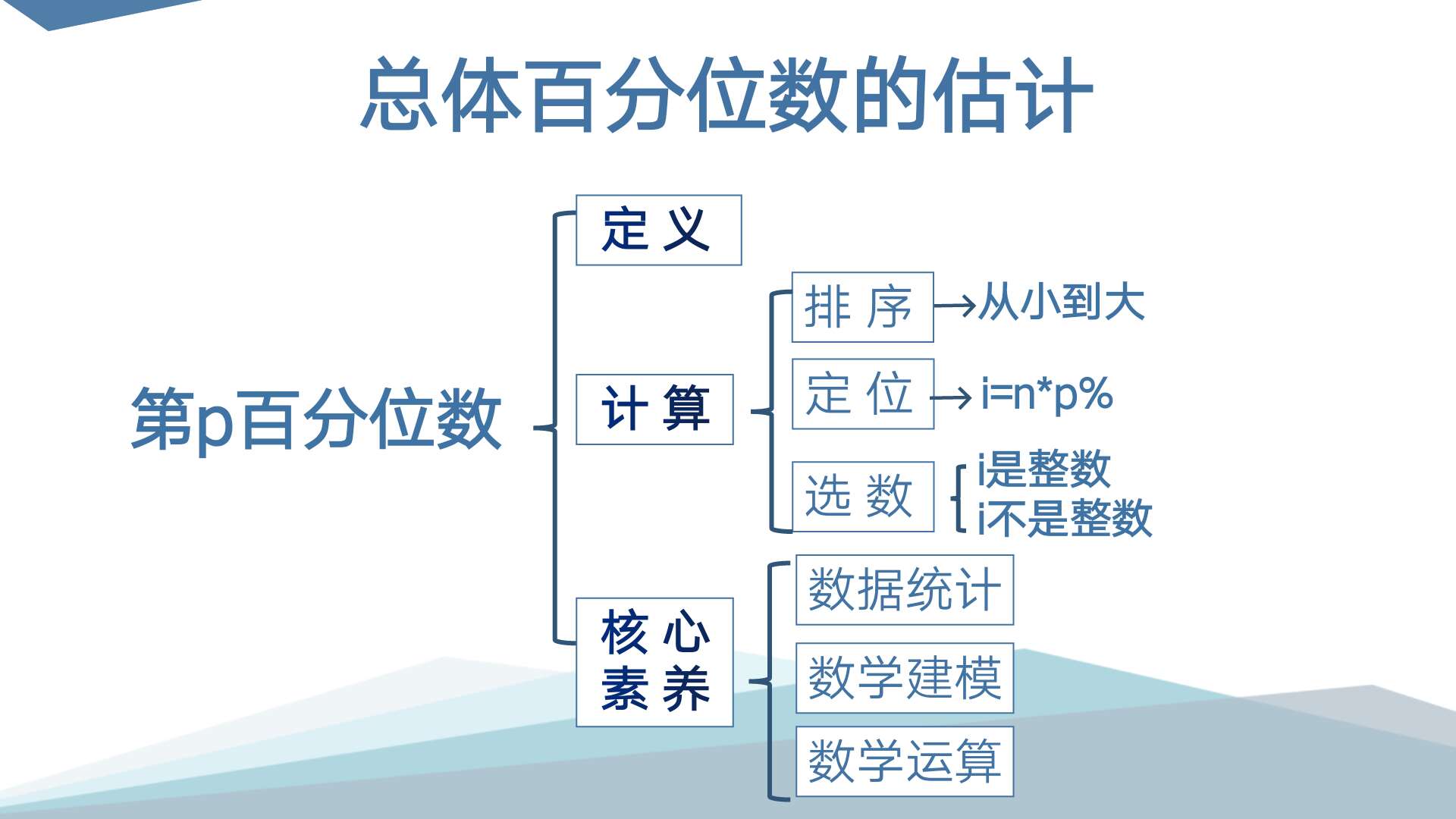
1、观看视频,了解有关新高考四选二科目赋分制,由赋分制的等级比例引入课题。
2、以教材中100位居民的月均用水量为例,探究新课。
思考1:关于北京市居民用水量的分析,我们上节课采用了哪些方法去进行数据分析?
<设计意图>旨在帮助学生回顾上节课频率分布直方图的操作流程和相关数据的寻找方法,让学生快速进入统计学习的状态,并为引出本节课的重点做铺垫
思考2:若希望80%的居民用户生活用水费支出不受影响,你能给市政府提出居民用户月均用水量标准应该如何制定的建议?
<设计意图>引导学生通过寻找中位数的方法联想寻找80%位数的方法,可水到渠成的得出本节重要定义。
思考3:怎样确定居民用户的月均用水量标准?
<设计意图>引导学生思考具体操作和该数据的意义。
『探究』请各小组讨论如何寻找a,并派代表给出方案?
<设计意图>团队合作、互帮互助,共同得出寻找a的方法和步骤,旨在帮助还未跟上节奏的学生能够在这个时间得到解惑,使在得出百分位数定义前形成个人理解。
思考4:在实际决策中,市政府把月均用水标准定为多少合适?
<设计意图>通过计算说明方案在实际操作中存在的偏差问题,统一思想。使同学们更精确的把握定义.
1、第p百分位数的定义:(学生探讨总结)
一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有__的数据小于或等于这个值,且至少有__
__的数据大于或等于这个值.
<设计意图>为使学生更好理解定义,特意将定义中两个重要数据挖空,能够增强学生记忆力和理解力。
2、总结求第p百分位数的步骤:(学生探讨总结)
计算一组n个数据的第p百分位数的步骤:
第1步,按__从小到大__排列原始数据.
第2步,计算i=n*p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的_平均数_.
思考5:中位数与第p百分位数有关系吗?
<设计图>意使学生体会中位数是特殊百分位数,百分位数是由中位数类比归纳得出的,更为得出四分位数的定义做了铺垫。
1、新高考赋分中小明化学成绩原始分为78分,赋分后为86分,则86分是所有成绩的第15百分位数的估计值吗?
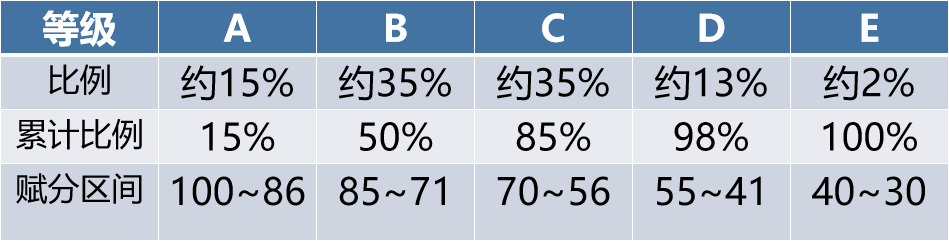
2、班级人数为50的班主任老师说“90的同学能够考取本科院校”,这里的“90
”是百分位数吗?
3、如何理解“这次数学测试成绩的第70百分位数是85分”这句话?
4、中位数与第P百分位数的关系是什么?
四分位数的定义:
25%,50%,75%这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数,其中第25百分位数也称为第一四分位数或下四分位数,第75百分位数也称为第三四分位数或上四分位数.
例1、随机选取2020年长沙空气质量指数(AQI)的30个样本数据:
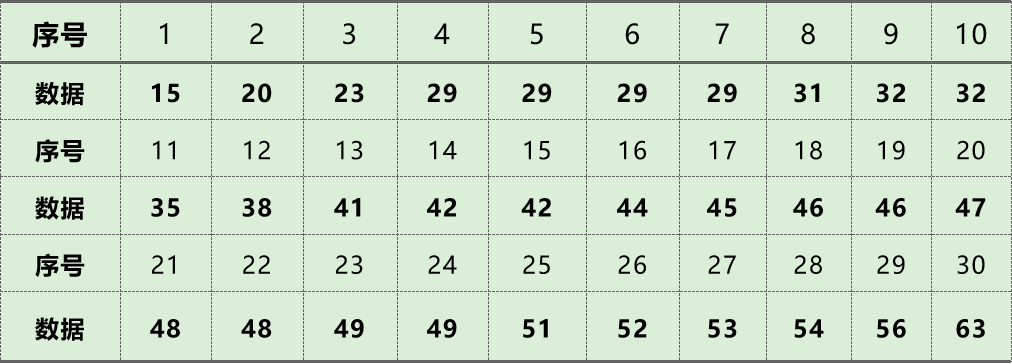
请估计2020年长沙市空气质量指数的第25,50,75百分位数。
例2 根据树人中学高一年级的386名女学生中按分层抽样的方法抽取了样本量为27的样本,如下:
163.0 164.0 161.0 157.0 162.0 165.0 158.0 155.0
164.0 162.5 154.0 154.0 164.0 149.0 159.0 161.0
170.0 171.0 155.0 148.0 172.0 162.0 158.0 155.5
157.0 163.0 172.0 160.0
估计树人中学高一年级女生的第25,50,75百分位数.
<设计意图>通过两个例题再次巩固定义的理解,并加深学生对求某样本的百分位数的步骤的记忆,规范解答。例1已经把数据进行了从小到大排序,例2需要学生自己排序,目的也是为训练学生分析数据的能力。
本节课要求了解第p百分位数的定义,掌握求第P百分位数的方法及步骤,会用样本的第P百分位数估计总体的第P百分位数。
<微判断>
1.若一组样本数据各不相等,则其75%分位数大于25%分位数.( )
2.若一组样本数据的10%分位数是23,则在这组数据中有10%的数据大于23.( )
3.若一组样本数据的24%分位数是24,则在这组数据中至少有76%的数据大于或等于24.( )
<微训练>
1.下列一组数据的第25百分位数是( )
2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6
A.3.2 B.3.0 C.4.4 D.2.5
2.下列关于一组数据的第50百分位数的说法正确的是( )
A.第50百分位数就是中位数
B.总体数据中的任意一个数小于它的可能性一定是50%
C.它一定是这组数据中的一个数据
D.它适用于总体是离散型的数据
1. 已知100个数据的第75百分位数是9.3,则下列说法正确的是( )
A. 这100个数据中一定有75个数小于或等于9.3
B. 把这100个数据从小到大排列后,9.3是第75个数据
C. 把这100个数据从小到大排列后,9.3是第75个数据和第76个数据的平均数
D. 把这100个数据从小到大排列后,9.3是第75个数据和第74个数据的平均数
2. 数据7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1的第30百分位数是_____________.
3. 求下列数据的四分位数
13,14,12,25,27,14,23,18,32,33,16,15,14,31,26
4. 从某珍珠公司生产的产品中,任意抽取12颗珍珠,得到他们的质量(单位:g)如下:
7.9,9.0,8.9,8.6,8.8,8.5,8.5,8.9,8.7,7.8,8.3,8.7
(1) 分别求出这组数据的第25,50,95百分位数;
(2) 请你找出珍珠质量较小的前15%的珍珠质量。
设为正确答案