- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《奇偶性》内容选自人教版A版第一册第三章第三节第二课时;函数奇偶性是研究函数的一个重要策略,因此奇偶性成为函数的重要性质之一,它的研究也为今后指对函数、幂函数、三角函数的性质等后续内容的深入起着铺垫的作用.
我们是普通高中,作为第一节奇偶性的新课,重在激发学生的学习兴趣,所以从形入手,从数结尾
1、理解函数的奇偶性及其几何意义;
2、学会运用函数图象理解和研究函数的性质;
3、学会判断函数的奇偶性.
重点:函数奇偶性概念的形成和函数奇偶性的判断;
难点:函数奇偶性概念的探究与理解.
奇偶性
奇偶性概念 例1 练习1 2 3
2. 奇偶函数的特点
巩固提升1 2 3
教学过程
情境导入:生活因对称而美,几个生活中关于对称的现实图形。(帮助学生把对称的现实带入到课堂)
一、课堂引入
数学因对称而丰富,几类大家见过的具有对称性的函数图像(帮助学生把对称的问题引入到数学问题中来)
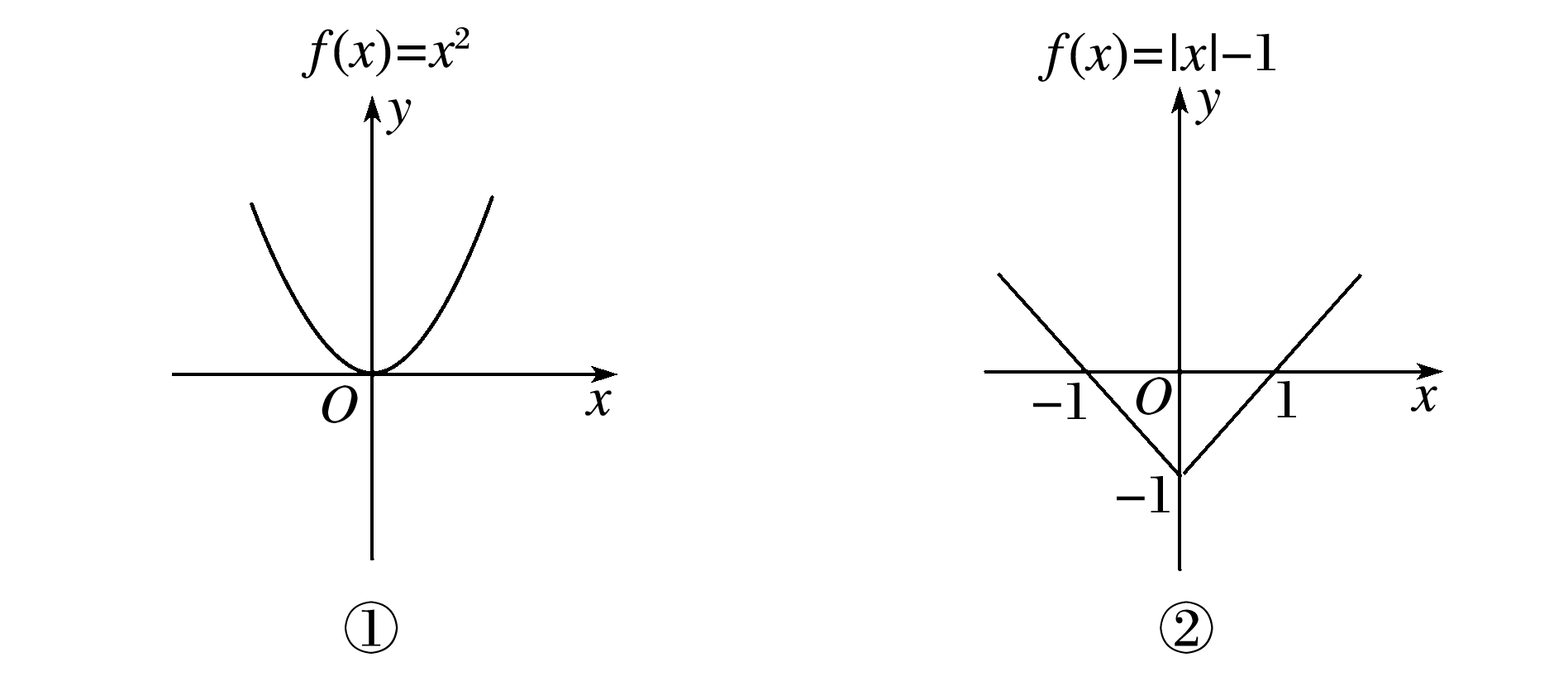
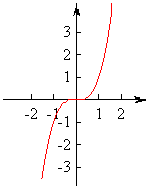
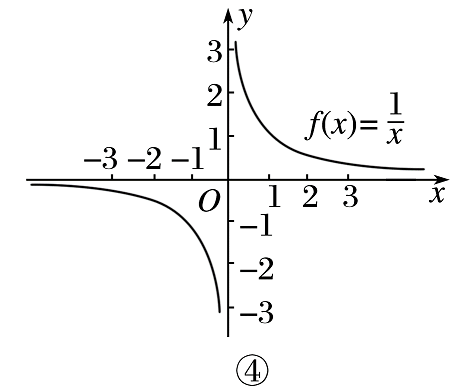
探究一、从形的角度理解奇偶性的定义
由上面的两个引入,让学生明白关于y轴对称,和关于原点对称的两种对称类型
二、新课讲授
函数奇偶性的定义:
直接切入定义:

马上由形的定义入手,从形的角度巩固奇偶性的知识 (帮助学生由新知转到简单题型)
例1、已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象.由点连线,提现函数的定义
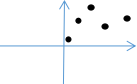
探究一、1.已知函数f(x)为偶函数,g(x)为奇函数,试将下列图形补充完整:巩固形的奇偶性
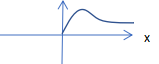

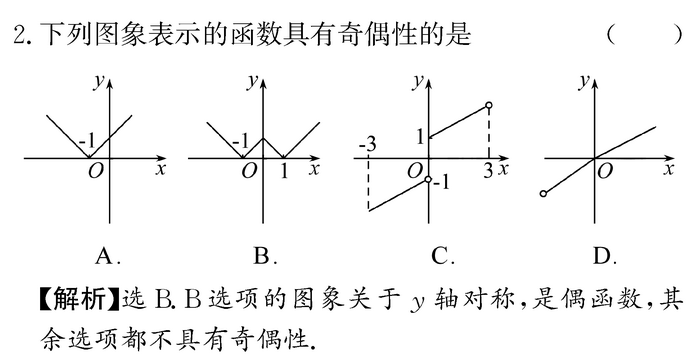
分析题目的时候,要提出定义域关于原点对称,强调。
探究二、奇偶性的定义(从数的方面解释奇偶性)
作出函数f(x)=x2图象,再观察表,你看出了什么?

由特殊到一般,观察f(-1)=f(1),f(-2)=f(2),f(-a)=f(a) 得到f(-x)=f(x)
偶函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),
那么函数f(x)就叫做偶函数.学生自己填空。
补充题:函数f(x)=x2,在x[-1,2]是偶函数么?引出一个关键地方,偶函数定义域必须关于原点对称!
自我探究:奇函数的定义(类比偶函数自我探究奇函数的定义)
作函数图形,观察有什么共同特征(小组讨论,学生上黑板演示)
从形和数两方面阐述,另外再引导学生推广到一般情况,得到奇函数的定义,也有学生填空
奇函数的定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.
小试牛刀:
例一.证明y=x4的奇偶性:(教师在黑板上板书规范格式)
练习:判断下列函数的奇偶性
(1)=
(2)
(3)
从定义的角度入手,解决上述问题,因为不能用特例法,和图形法来解决,第三小题也可以用图像
然后设置几何画板,做出上面四个图形,然让同学们从形的方面与定义印证,加深认识
巩固提升(帮助学生从形,数,定义三方面认识函数的奇偶性)
1、如果定义在区间[3-a,5]上的函数f(x)为奇函数,则a =_____
2、若函数在R上为偶函数,求m的值
3、
设为正确答案