- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本单元主要教学圆柱和圆锥的认识、圆柱的表面积、圆柱的体积和圆锥的体积。要求学生认识圆柱和圆锥,掌握它们的基本特性,以及圆柱的侧面积、表面积的计算方法和圆柱、圆锥体积的计算公式,会运用所学知识解决一些简单的实际问题,培养学生解决问题的能力。教材在引导学生整理这些知识的时候,始终注意引导学生把握圆柱与圆锥的联系与区别,使学生更加明晰相关概念,灵活运用计算公式,使学生在经历观察、操作、推理、想象过程中认识并掌握相关知识,进一步发展学生的空间观念。
本单元根据学生的生活经验认识了圆柱和圆锥,学生基本已经具备了整理和复习知识的经验,部分学生可能欠缺抓不住复习的重点和难点,整理知识不够全面系统,没有顺序等。因此,教师在教学中要善于引导同学们区系统有序的整理知识,学生的好奇心很强,教学中可以利用学生的好奇心理和求知欲望,引导学生运用所学知识解决实际问题。
知识与技能:通过整理和复习,使学生进一步认识圆柱、圆锥的特征,掌握圆柱表面积、体积,圆锥体积的计算方法。
过程与方法:掌握圆柱表面积、体积,圆锥体积的计算方法。
情感态度与价值观:综合运用所学知识,灵活地解决与圆柱、圆锥有关的数学问题。
【教学重点】归纳整理有关圆柱和圆锥的知识,形成知识体系。
【教学难点】综合运用所学知识,灵活地解决与圆柱、圆锥有关的数学问题。
《圆柱和圆锥的整理与复习》教学设计
教学目标:
知识与技能:通过整理和复习,使学生进一步认识圆柱、圆锥的特征,掌握圆柱表面积、体积,圆锥体积的计算方法。
过程与方法:掌握圆柱表面积、体积,圆锥体积的计算方法。
情感态度与价值观:综合运用所学知识,灵活地解决与圆柱、圆锥有关的数学问题。
教学重点:归纳整理有关圆柱和圆锥的知识,形成知识体系。
教学难点:综合运用所学知识,灵活地解决与圆柱、圆锥有关的数学问题。
课前准备:学生对本单元的知识进行复习和整理。教师:相关课件和练习题。
教学方法:自主探究法、练习法。
教学过程:
一、揭示课题:
师:(多媒体课件)猜猜我是谁?(圆柱),这个呢?(圆锥)。圆柱和圆锥是我们这学期第三单元学习的知识,今天我们共同把这部分知识进行整理和复习。板书课题:圆柱和圆锥的整理与复习
二、共同参与、展示、评议
1、师:同学们,翻开课本快速浏览本单元,看看这一单元中,我们共同学习了有关圆柱和圆锥哪些方面的内容?(师生共同对这部分知识利用树形进行了梳理,构建完善的知识框架。)
2、复习圆柱和圆锥的特点及有关计算公式
1)、复习圆柱、圆锥的特征:
圆柱是立体图形,柱有上、下两个面叫做底面,它们是完全相同的两个圆.两个底面之间的距离叫做高.侧面是一个曲面。
2)、圆锥有哪几个部分?有什么特点?(是立体图形,有一个顶点,底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离,叫做圆锥的高。)
3)、复习基本公式:
圆柱的侧面积怎样计算?(底面的周长×高)为什么要这样计算?(因为:底面的周长=长方形的长,高=长方形的宽)
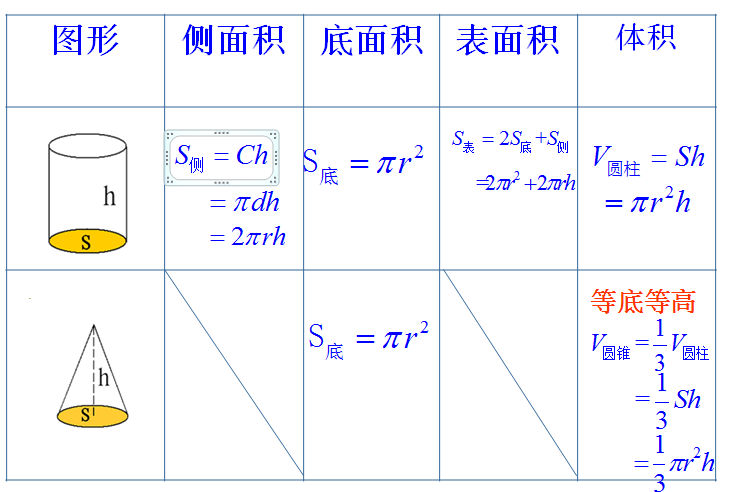
表面积是由哪几部分组成的?(圆柱的侧面积+两个底面的面积) 圆柱的体积怎样计算?(底面积×高)计算公式是怎样推导出来的?(把圆柱切割开,拼成近似的长方体,使圆柱体的体积转化为长方体的体积。根据长方体的体积=底面积×高,推出圆柱体的体积=底面积×高)圆柱体的体积计算的字母公式是什么?(V=Sh)
怎样计算圆锥的体积?(用底面积×高,再除以3),计算圆锥体积的字母公式是什么?(V=1/3Sh),为什么这样计算?
4)、圆柱和圆锥有怎样的关系?
等底等高的圆锥体积是圆柱体积的三分之一。 等底等高的圆柱体积是圆锥体积的三倍。
三、巩固所学内容,进行分层练习。
(谈话:可见同学们对这个单元的知识掌握不错,接下来老师想通过练习来挑战你们对所学知识掌握的情况,你敢挑战吗?
(1)把一个底面周长是12.56厘米的圆柱侧面展开,得到一个正方形,这个圆柱的高是( 12.56 )厘米。
(2)把一个体积为24立方分米的圆柱形木块,削成一个最大的圆锥,则圆锥的体积是( 8 )立分方米,若这一个圆锥体的底面积是6平方分米,它的高是( 4 )分米。
(3)做一节底面周长是3分米,长4米的圆柱形通风管。至少需要铁皮( 120 )平方分米 。
(4)把一个高为20分米的圆柱体截成4个小圆柱,则增加(6 )个底面积,若表面积增加了18 平方分米,则原来圆柱的体积是( 60 )立方分米。
(5)一台压路机的前轮是圆柱形,轮宽2m,直径1m,工作时每分钟滚动20周。
①、这台压路机工作1分钟前进( 62.8 )米。
3.14×1×20=62.8(m)
②、工作1分钟压过的路面面积是( 125.6 )平方米。
3.14×1×2×20=125.6(㎡)
2、选一选
(1)用一块边长31.4分米的正方形铁皮,配上半径是( C )分米的圆形底面就能做成一个最大圆柱体容器。 A. 10 B. 4.71 C . 5
(2)在下列图中,以直线为轴旋转一周,可以得到圆柱体的是(A ),得到圆锥体的是( B )。
A B C
(3)圆柱的底面半径扩大到原来的2倍,高缩小到原来的 , 它的体积( A )。
A .扩大到原来的2倍 B .缩小到原来的 C .不变
(4) 在一个半径是10厘米的圆柱形容器中, 放入一个圆锥形铁块,全部浸没在水中,这时水面上升0.6厘米。
①这个圆锥形铁块的体积是( B )立方厘米。
A.3.14×102×0.6÷3=62.8
B. 3.14×102×0.6=188.4
C. 3.14×102×0.6×3=565.5
②若这个圆锥形铁块的高为6厘米,它的底面积是( F )平方厘米。
D. 31.4 E. 314 F. 94.2
(5).把一个棱长是2分米的正方体削成一个最大的圆柱体,它的侧面积是( B )平方分米。 A. 6.28 B. 12.56 C. 25.12
四、拓展提高
一个圆柱的底面直径是4厘米,如果沿着底面直径把这个圆柱切成大小相等的两个半圆柱,表面积增加40平方厘米.这个半圆柱的表面积是多少平方厘米?
(设计意图:让学生提出问题,解决问题,培养学生的问题意识,学生在宽松、轻松开放的情境中感受到数学的魅力,提高思维的灵活性。实现生生间,师生间的交流互动,共同促进。)
五、分享收获,畅谈感想
这节课,复习了哪些方面的内容?你学得最好的内容是什么?还有什么不明白的地方吗?
设为正确答案