- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课是湘教版版八年级上册第二章第五节全等三角形的第三个判定定理。是在学习完SAS、ASA的基础上,由ASA推论所得。三角形是最常见的几何图形之一,在日常生活中有着广泛的应用。在知识结构上,等腰三角形,直角三角形,线段的垂直平分线,角的平分线等内容都可以通过证明两个三角形全等来加以解决;在能力培养上,无论是逻辑思维能力,推理论证能力,还是分析问题解决问题的能力,都可在全等三角形的教学中得以提高。而且证明全等三角形是证明线段相等和角相等的重要手段,本节课作为证明两个三角形全等的依据之一,是本章的重中之重。教材上例题图形的构成,可分为旋转型、轴对称型、中心对称型、旋转对称型等,需要学生们具有一定的想象能力、较强的图形意识。在书写推理过程中,需要前面所学的知识为铺垫,如线段的中点性质、角的角平分线性质、等腰三角形等角对等边或者等边对等角,还有七年级学过的同角的余角相等、同角的余角相等。其实,就是说,凡是学过的几何图形中包含相等关系或者能得出相等关系结论的,在书写证明过程时,都会用得到。把三角形的全等,学的越扎实,将会为三角形的相似,以及学习四边形、圆等打下基础。
学生现在处于几何推理论证的初步阶段,从这章开始,学生应该逐步学会几何证明,几何证明题的推理证明的书写对学生来说难度较大,不仅要求格式规范,更重要的是思路清晰、有理有据,简洁严谨。同时,学生以前学习的几何都是一些简单的图形,从这章开始出现了几个图形的变换或叠加,学生在解题过程中,准确剥离所求两个三角形,并找准两个三角形全等的条件将会是一个难点,前面学生已经学习了边角边、角边角定理,找对应边、对应角相等有了一定的基础,因此在运用角角边定理时,找出证全等的一到两组边或角对应相等的条件后,寻找或证明第三组条件是需要突破的难点。
1.知识与技能:
(1)经历探索三角形全等条件的过程,体会利用操作、归纳获得 数学结论的过程,培养学生观察分析图形能力、动手能力。
(2)掌握两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS)定理的推导并过程熟记角边角定理的内容。
(3)能运用角边角定理证明两个三角形全等。
(4)通过对问题的共同探讨,培养学生的协作、交流能力
2.过程与方法:
(1)经历探索三角形全等条件的过程,培养学生观察分析图形能办动手。
(2)在例题处理过程中组织引导学生自主探究、分析讨论、交流解法,巩固三角形全等的证明方法。
(3)在习题交流中通过观察几何图形,培养学生的识图能力。
3.情感、态度与价值观 :
(1)在探索三角形全等条件的过程中,培养学生有条理的思考能力概括能力和语言表达能力。
(2)培养学生善于思考、积极参与数学学习活动、勇于探索的钻研精神及作交流的意识。
(3)在教学过程中,使学生获得用所学数学知识解决实际问题的成功体验,提升用数学的意识。
教学重点:根据角边角定理证推导出角角边定理的过程和角边角定理的应用;
教学难点:引导学生找出证明两个三角形全等的条件,培养学生的思维能力。
角角边定理
在△ABC和△A′ B′ C′中,
∠A=∠A′ ,
∠B=∠B′ ,
BC= B′C′ ,
∴ △ABC≌△ A′ B′ C′ (AAS)
1.前面我们学习了哪些全等三角形的判定方法?
2.如果在△ABC和 △A'B'C' 中,如果
∠B= ∠B′,BC=B'C',根据我们学过的全等三角形的判定方法,还缺少一个条件,请你补充一个条件,使这两个三角形全等。并说明根据是什么?
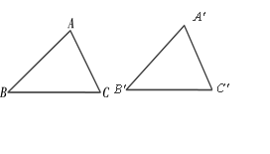
估计学生会考虑补充:∠C=∠C’(角边角),或者AB=A’B’(边角边)
如果填:∠A=∠A’能否判断△ABC和△A’B’C’全等?
1.角角边定理
(1) 讨论上面问题
∵∠A+∠B+∠C=∠+∠+∠=180°,∠B=∠,∠A=∠A’
∴∠C=∠C’,又BC=B’C’,
∴△ABC≌△(ASA)
(2)现在再换一个条件,把BC=B’C’换成AB=A’B’,这两个三角形还全等吗?
(3)由此我们可以得出什么结论?试着自己归纳一下。
角角边定理:两角分别相等且其中一组等角的对边相等的两个三角形全等。(简写为:角角边,或者:AAS)
2. 应用格式
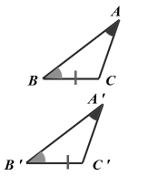
在△ABC和△A′ B′ C′中,
∠A=∠A′ ,
∠B=∠B′ ,
BC= B′C′ ,
∴ △ABC≌△ A′ B′ C′ (AAS)
小结:写全等五行时,等号两边对应的字母要放在对应的位置,以及三个条件的摆放顺序要按照定理内容的顺序。
3. 尝试应用
判断下列各对三角形是否全等,如全等,说出理由。

例1 已知:如图,∠B=∠D,∠1=∠2,求证:△ABC≌△ADC.
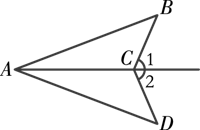
证明 ∵∠1 =∠2,
∴∠ACB=∠ACD(同角的补角相等).
在△ABC和△ADC中,
∠B =∠D,
∠ACB =∠ACD,
AC = AC,
∴ △ABC≌△ADC (AAS)
例2 已知:如图,点B,F,C,E在同一条直线上,AC∥FD,∠A=∠D,BF=EC.求证:△ABC≌△DEF.
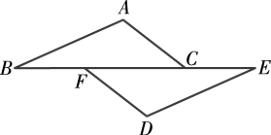
证明: ∵ AC∥FD,
∴∠ACB =∠DFE.
∵ BF= EC,
∴ BF+FC=EC+FC,
即 BC=EF .
在△ABC 和△DEF中,
∠A =∠D,
∠ACB =∠DFE,
BC = EF,
∴ △ABC≌△DEF(AAS)
1. 已知:如图,∠1=∠2,AD=AE. 求证:△ADC≌△AEB.

证明:
∵ 在△ADC 和△AEB中,
∠1 =∠2,
∠A =∠ A,
AE= AD,
∴ △ADC≌△AEB(AAS).
2. 已知:在△ABC中,∠ABC =∠ACB, BD⊥AC于点D,CE⊥AB于点E.求证:BD=CE.

如图,已知△ABC ≌△A′B′C′ ,AD、A′D′ 分别是△ABC 和△A′B′C′的高.试说明AD= A′D′ ,并用一句话说出你的发现.
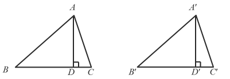
解:∵△ABC ≌△A′B′C′ ,
∴AB=A'B',∠ABD=∠A'B'D'.
∵ AD⊥BC,A'D'⊥B'C',
∴∠ADB=∠A'D'B'=90°.
在△ABD和△A'B'D'中,
∠ADB=∠A'D'B'(已证),
∠ABD=∠A'B'D'(已证),
AB=A'B'(已证),
∴ △ABD≌△A'B'D'.
∴ AD=A'D'.
小结:全等三角形对应边上的高也相等。
思考:1.全等三角形对应中线相等吗?全等三角形对应角平分线相等吗?请课后验证。
2.SAS、ASA、AAS三个定理中,需要有1-2个角相等的条件,那么,三组对应边分别相等能证全等吗?三组对应角分别相等呢?你能由此再得出什么结论吗?
这节课你学到了什么?
AAS使用的方法总结: 1.如果已知两个三角形的一边一角对应相等,且边为角的对边,若再能找出一组角对应相等,则用AAS来判定这两个三角形全等; 2.如果已知两个三角形的一边一角对应相等,且边为角的邻边,若能判断出这条边的对角相等,则也用AAS来判定这两个三角形全等; 3.如果已知两个三角形的两组角对应相等,若再能找出任意一边对应相等,则也用AAS来判定这两个三角形全等; 4.如果已知两个三角形的一边一角对应相等,且边为角的邻边,若能找出夹边的另一角对应相等,则用ASA来判定这两个三角形全等; 5.如果已知两个三角形的两组角对应相等,若能这两组角的夹边对应相等,则也用ASA来判定这两个三角形全等.
3. 你还有什么疑问吗?
设为正确答案