- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本单元教材第一次安排了简单的集合思想的教学,涉及的重叠问题是日常生活中应用比较广泛的数学知识。集合思想的引入为培养学生的逻辑思维能力提供了良好的素材。今后的学习也经常能应用到韦恩图表示关系。
在此之前,学生已经学习过分类的思想方法,但集合这部分内容比较抽象,在这里是让学生通过生活中容易理解的例子去初步体会集合思想,学生只要能够用自己的方法解决问题就可以了。
1.理解集合圈里各部分的意义。
2.会读集合圈中的信息,会按条件填写集合圈。
3.学生会借助直观图,利用集合的思想方法解决简单的实际问题。
1.会读集合圈中的信息,会按条件填写集合圈。
2.学生会借助直观图,利用集合的思想方法解决简单的实际问题。
师:同学们,你们喜欢玩游戏吗?脑筋急转弯,比比谁反应快?
游乐园里两对母女在拍照,但是只有三个人,这是怎么回事?(强调妈妈身份的双重性--身份“重复/重叠”了)
师:在生活中这种现象有很多,我们经常会遇到,今天我们一起走进数学广角,来研究这些有趣的重叠问题。(板书:重叠)
(一)创设情境,引出新知
师:同学们,秋季运动会马上要来了,老师昨天收集了咱们1804班报名参加跳绳、踢毽比赛的学生名单。跳绳的有9人,踢毽的有8人。请问参加这两项比赛的共有多少人?(一部分学生说17人;一部分学生有质疑,要看看具体名单)
2、出示学生名单
下表是1804班参加跳绳、踢毽比赛的学生名单:
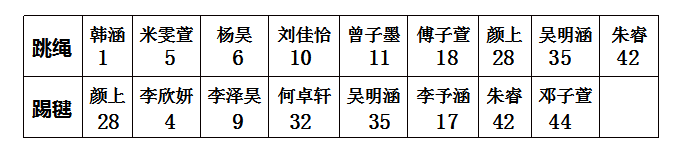
问:现在你知道参加这两项比赛的共有多少人了吗?(14人)
问:这是怎么回事呢?
(原来有几人既参加了跳绳,又参加了踢毽,重复的人只能数一次!)
是不是只能数一次?接下来我们把这几位小选手请上来就知道了,这三位同学一会在左边一会在右边为什么?
(因为这三位同学既参加的跳绳又参加了踢毽,不知道应该在哪)
师:接下来邀请同学们做设计师,你可以用学号表示这些同学,看看有没有一个好办法,帮这三位同学找到合适的位置,能让人一眼就清楚地看出是哪几人重复呢?
(可以连一连、画一画、圈一圈或者其他方式,请同学们两人为一个小组进行合作设计)
(二)自主探究,学习新知
1.小组合作探究
2.汇报交流,选择有代表性的方案全班交流
预设1:用连线的方法表示
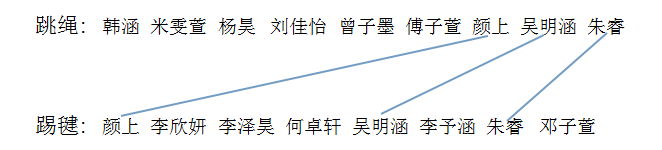
预设2:用表格整理出来
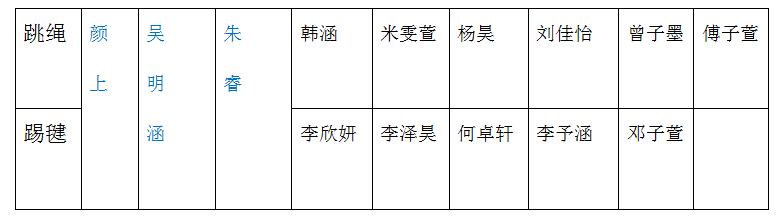
预设3:按分类整理出来
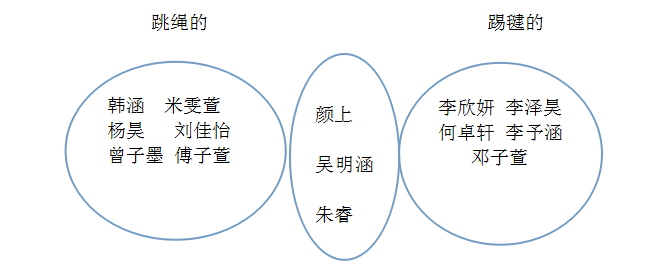
(三)对比分析,介绍集合以及维恩图
1.对比、分析
师:同学们解决问题的能力真强,能用想到这么多办法来解决问题。
比较这几种方法,你更喜欢哪一种,为什么?
预设1:喜欢第三幅,去掉了重复的学生的姓名,更清楚,很容易看出参加这两项比赛的学生情况。
预设2:喜欢第三幅,用两个椭圆的重叠部分表示两项比赛都参加的学生,很直观。
那么我们一起把这位同学的作品完成到黑板上。
(板书;两项都参加的学生,跳绳的学生,踢毽的学生,板书完让学生一起说一说各个部分分别表示什么意思)
2.介绍维恩图表示集合
师:同学们,你们研究出的这个内容就是我们今天要学习的知识,数学广角---集合。这样的一幅图有一个数学名字叫集合图,早在1881年,英国数学家韦恩就创作出了这样的图,他的这个发明为集合的研究带来了极大的方便,为了纪念他,人们又把集合图叫做“维恩图”
(四)列示解答,加深对集合运算的认识
师:根据维恩图,现在你能用数学算式解决我们一开始的问题:
参加这两项比赛的一共有多少人?
(1)尝试独立解决。
(2)汇报交流,体会解决问题的多种方法。
预设:9+8-3=14,9+(8-3)=14,8+(9-3)=14,6+3+5=14等。
(让学生通过图示与算式结合进行表达,感悟多种集合知识、可以让学生在维恩图上指一指它们求出的是哪一部分;指一指算式中每一步表达的是哪一部分,如“8-3”和“9-3”。)
师小结:在计算总人数时,要记得找出重复的人数,计算时,要把重复的人数减去。
师:下面我们就用今天学习的新知识来解决实际问题
打开书本第105页完成做一做1、2小题
学生独立完成,请同学上台来说一说你的想法。
(一)举例生活中的重叠
师;同学们真了不起,看来你们都真正明白了韦恩图各部分的含义了,其实像这样的重叠问题在我们的生活中应用的非常广泛,仔细想想,在哪里用到了?
生1:我既是1804班的学生,还是青园中信的学生;
生2:我既是会唱歌的人,又是会跳舞的人;
(二)谈谈这节课的收获。(理解集合图中每部分的含义,能解决简单的有重复部分的问题。)
设为正确答案