- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课选自《普通高中课程标准实验教科书数学必修1(人教A版)》中的第三章的3.2.2函数模型的应用实例。通过对前一节的学习,学生对常见函数模型,如一次函数模型,二次函数模型,指数函数模型,对数函数模型,分段函数模型有了基本的认识。教科书用4个例题做示范,并配备了较多的实际例题进行练习。在4个例题中,分别介绍了分段函数,指数函数,二次函数的应用,在例4和例6还渗透了函数拟合的基本思想,让学生感受函数模型的建立过程和方法,体会函数在实际生活中的应用,认识到函数是描述客观世界变化规律的基本数学模型,并能初步建立函数模型解决现实生活中的一些简单问题。
1.知识经验:学生熟悉一次函数、二次函数、指数函数、对数函数、分段函数等函数的基本性质,会画出大致的草图;
2.生活经验:生活中遇到的一些实际问题,通过在理想状态下建立简单的函数模型,解决实际问题;
3.技能态度:①用数学的眼光观察世界的能力——比如:学会审题,理解题意,找出题意中的数量关系②会用数学的思维思考世界的能力——比如:通过收集数据,利用Excel画出散点图,得到函数模型③用数学的语言表达世界的能力——比如:通过对简单函数模型的建立、求解、检验,从而解决简单的实际问题。
4.性格特点:高一学生自我效能感较强,有较好的交流意识和合作能力,求知欲较高。
SWORT |
分析 |
S(Strengths) |
高一学生对Excel表格、几何画板的应用好奇心强,求知欲较高,有较好的交流意识和合作能力,参与课堂的活动积极性高;学生已学习了一次函数、二次函数、指数函数、对数函数、分段函数等函数,了解基本的函数性质,并会画出大致的草图,具备了数形结合的数学思想。 |
优势 |
|
W(Weaknesses) |
由于存在一部分是在乡镇学校毕业的初中生,升入高中后对信息技术的应用较生疏;如何合理的分析、处理数据的能力有待加强;根据面临的实际应用问题抽象为数学问题,完成从文字语言、图表语言向符号语言的转化的意识还不够;构建简单的函数模型解决实际问题的能力有待加强。 |
劣势 |
|
O(Opportunities) |
本节课《3.2.2函数模型的应用实例》是对基本初等函数性质的延续和发展,通过利用信息技术实现对现实情境中收集的数据进行观察,分析,利用Excel表格拟合出较为接近的函数图像模型,再计算出拟合函数模型的表达式(或者直接由散点图上的趋势线生成函数的表达式),检验,最后应用所选择的模型解决实际问题,为以后的数学建模和探究活动奠定了基础. |
机会 |
|
T(Threats) |
提高学生应用拟合函数模型解决生活中简单的实际问题的应用意识和应用能力是教师面临的挑战。 |
挑战 |
(一)知识与技能目标
1.学生能够找出简单实际问题中的函数关系式,在课堂内渗透数形结合的思想,使学生能更好的了解常见的函数模型;
2.学生能够从生活经验和数学直观出发,了解生活中的基本函数模型的应用;
3.利用Excel表格画出散点图并构造函数模型,会利用建立的函数模型解释有关现象或对有关发展趋势进行预测;
(二)过程与方法目标
1.向学生展示散点图,让学生感受基础的函数模型;
2.通过例题的讲解,引导学生经历解决实际问题的全过程,让学生初步掌握应用函数模型的思想和方法;
3.采用小组合作学习、探究学习的方式,培养学生“竞争与合作”的精神;
4.渗透数形结合思想、转化与化归思想、方程组思想等。
(三)情感态度价值观
1.感受数学与生活的密切联系,激发学生学习数学的兴趣、提升学生对生活的热爱;
2.通过拟合函数模型的建立,培养学生勇于探索、勤于思考的精神;
3.学科核心素养:
a.数据分析:通过数据分析画出散点图;
b.数学抽象:由实际问题建立函数模型;
c.数学建模:由散点图构造函数模型;
d.逻辑推理:检验后、选择合适的函数模型;
e.数学运算:代入点的坐标求出函数解析式;
f.直观想象:运用函数图形分析问题。
重点:通过对给出数据进行分析,利用Excel画出表格中数据的散点图,抽象出相应的函数模型,求出函数模型的解析式;
难点:根据面临的实际应用问题抽象为数学问题,完成从文字语言、图表语言向数学符号语言的转化,并检验函数模型的合理性,应用函数模型解决实际问题。
3.2.2函数模型的应用实例
建立拟合函数模型、解决实际问题的基本过程:
1.收集数据;
2.画散点图;
3.建模;
4.求模;
5.检验;
6.结果。


什么是数学建模?
设计意图:向学生展示《中国大学生数学建模竞赛》图片,吸引学生的注意力;再通过视频展示有关数学建模知识,激发学生学习的好奇心,调动学生学习的主动性。
1.在前面学习的函数模型应用实例中,常见的函数模型有哪些?

2.在前面学习过的函数模型应用实例中,我们解决了哪两类简单的实际应用问题?
(1)利用给定的函数模型解决实际问题;
(2)建立确定性的函数模型解决实际问题。
3.你能说出下列散点图符合哪种函数模型吗?
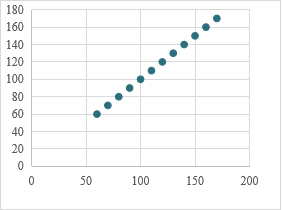
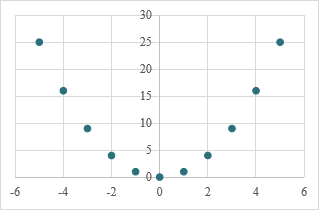
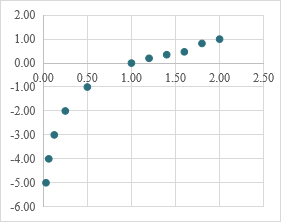
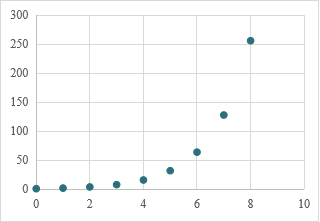
设计意图:以问题串的行式层层设问,让学生回忆起所学的函数模型,教师自己设计数据,利用Excel表格画出散点图,培养学生直观想象的核心素养,通过散点图抽象出函数模型,为例题中对数据转化为散点图的处理做好铺垫。
1.解决函数应用问题的基本步骤有哪些?
2. 同学们觉得自己的身材怎么样?是偏胖?偏瘦?还是标准体重?
设计意图:学生对如何解决身边的问题,有着很大的参与度,以学生自己的身材如何设问,吸引了学生学习的注意力、引导学生主动思考;通过学生的自主思考,发散了学生的思维,引导学生自主回顾建立函数模型解决实际问题的基本步骤,让学生明白学习数学的社会应用价值,明白学习数学是有用的。
例:某地区不同身高的未成年男性的体重平均值表:
身高/cm |
60 |
70 |
80 |
90 |
100 |
110 |
体重/kg |
6.13 |
7.90 |
9.99 |
12.15 |
15.02 |
17.50 |
身高/cm |
120 |
130 |
140 |
150 |
160 |
170 |
体重/kg |
20.92 |
26.86 |
31.33 |
38.85 |
47.25 |
55.05 |
(1)根据表格数据,请你利用Excel画出表格中数据的散点图?
(2)通过观察散点图,你建立了体重y kg与身高x cm的哪种函数模型?
(3)试写出你建立的体重y(kg)与身高x(cm)的函数模型的解析式;
(4)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,请同学们判断该地区一名身高为175 cm体重为78 kg的在校男生的体重是否正常?
设计意图:这个例题是对教材105页例题6的改编,通过添加适当的设问方式,符合学生的认知规律,回归教材,该题以学生生长发育为背景,与学生的实际生活紧密相连,渗透了函数拟合的思想。让学生经历建立数学模型的过程,培养学生数形结合的思想;通过对该例题的讲解,培养了学生数据分析、数学建模、数学运算、直观想象等核心素养。引导学生通过excel表格画出表格数据的散点图,拟合出散点图的大致趋势线,学生通过对比选取合适的函数模型,利用计算器求解得到拟合函数模型的解析式,通过解析式对身边男生的体重是否正常进行判断,体现了数学的应用价值,有利于进一步激发学生学习数学的兴趣,促进学生逐步形成和发展数学应用价值,提高实践能力。
建立拟合函数模型,解决实际问题的基本过程:
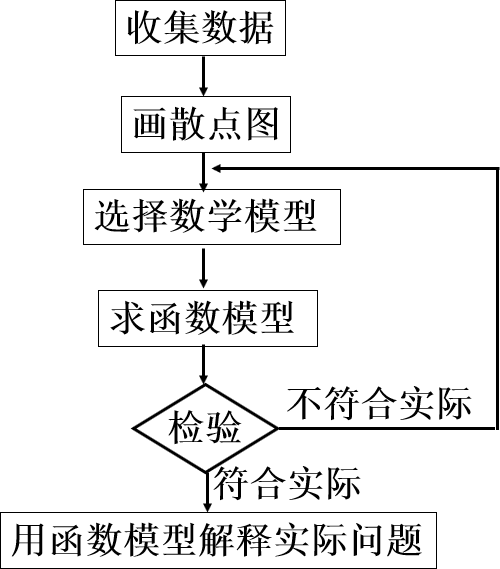
设计意图:通过对例题的求解,让学生体验建立拟合函数模型,解决实际问题的过程,及时自我小结,为解决当堂练习提供了思路。引导学生及时自我小结,注重反思提高,寻求规律方法,提高学习效率。
(教材107页B组第一题改编)党的十九大提出:
——到2020年全面建成小康社会,实现第一个百年奋斗目标;
——到2035年基本实现社会主义现代化;
——到本世纪中叶全面建成富强民主文明和谐美丽的社会主义现代化强国。
我国 2010年—2019年的国内生产总值(GDP)数据如下表所示:

美国 2010年—2019年的国内生产总值(GDP)数据如下表所示:

(1)利用Excel画出散点图,以小组合作探究的方式分别建立一个能基本反映这一时期中国、美国国内生产总值发展变化的函数模型;
(2)通过建立的函数模型,请你预测一下我国国内生产总值有可能超过美国内生产总值吗?如果有可能,那么请你预测中国的GDP是在哪一年超过美国的GDP的;如果没有可能,请说明理由。
设计意图:当堂练习是对教材习题的改编,回归了教材,深入研究了教材;结合习近平总书记的讲话精神,以党的十九大为背景,展示了中国近10年的GDP数据,展现了中国快速发展的经济实力,让学生树立民族自信心和自豪感。由中、美两国近10的国内生产总值(GDP)数据,观察数据对比分析,以及对数据的合理处理,培养了学生数学分析的核心素养;学生在例题中经历了拟合函数的建立过程,学生能够较快的处理这些数据,通过制作散点图,拟合函数模型,构建函数模型,符合学生的认知规律;在学生的最近发展区设置练习,能够有效的提高学生的课堂效率培养学生数学建模的核心素养。再将小组间共同探究所得的预测结果由小组代表在讲台上操作出来,利用Excel表格和几何画板得到预测的结果(体现了对信息技术的应用),再次通过观看微视频(利用信息技术,用爱剪辑软件拼成一个视频),从国际专业人士进行大数据分析后得到的预测结果告知学生中国的GDP在2028年超过美国的GDP,从而培养了学生的爱国主义情怀,也展现了我国国力越来越强盛,增强了学生的民族的自豪感和自信心。
本堂课你的收获是什么?
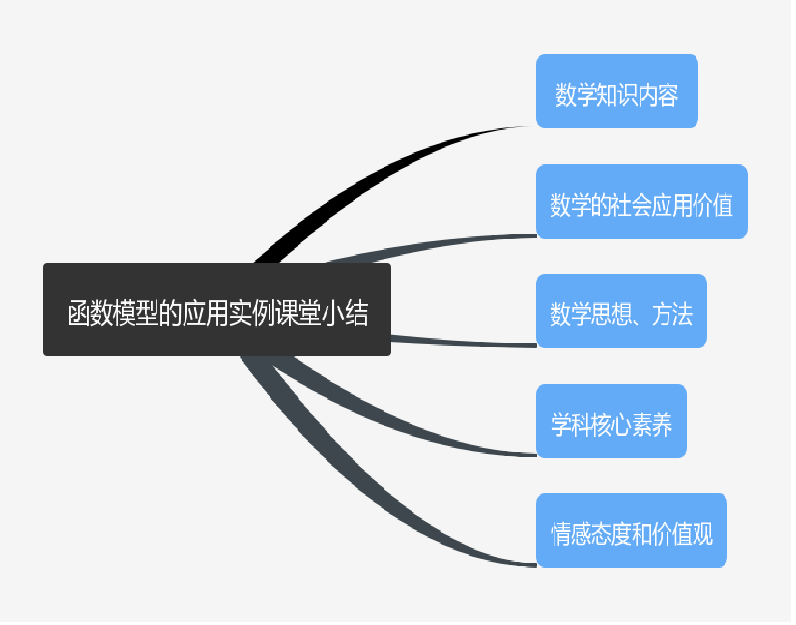
设计意图:在学生回答收获的过程中,以思维导图的行式进行分类总结,引导学生利用思维导图,完善自己的知识结构,提高学习效率。从预测的数据中可知,我国会在2028年超过美国的国内生产总值,成为世界第一经济体,激发了学生的民族自信心和自豪感,培养了学生的爱国主义情怀。
![]()


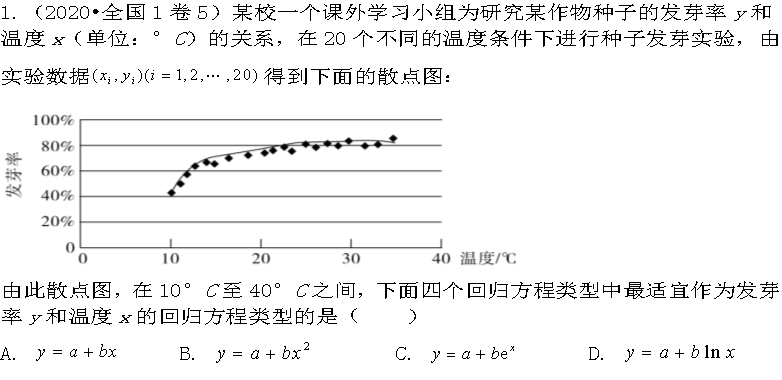
设计意图:以今年的高考真题作为课后练习,让学生明白高考考查函数模型应用实例的题型。
设为正确答案