- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



勾股定理是初等几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系,是直角三角形中的一条重要性质。勾股定理是欧氏平面几何的一个核心结果,是三角学的出发点,与“黄金分割”一起被开普勒称为“几何学的两个宝藏”。它在直角三角形的三条边之间建立了固定关系,使人们对几何感性的认识精确化,体现了"数形结合"思想,启发了人类对数学的深入思考,促成了代数和解析几何的结合,影响了数学思考模式。勾股定理是解决直角三角形中的计算问题和解直角三角形的主要依据之一,同时在实际生活中具有广泛的用途。教材是从等腰直角三角形出发,再把一般直角三角形放在方格纸上,可体现从特殊到一般的数学思想,呈现反映了勾股定理的三个层面:知道勾股定理,证明勾股定理,再发现勾股定理。
八年级学生已经初步具有几何图形的观察,几何证明的理论思维能力。他们希望老师创设便于他们观察的几何环境,给他们发表自己见解和表现机会,希望老师满足他们的创造愿望,让他们实际操作,使他们获得施展自己创造才能的机会。对于勾股定理的得出,首先需要学生通过动手操作,在观察的基础上大胆猜想数学结论,这需要学生具备一定的分析、归纳的思维方法和运用数学的思想意识,但学生在这一方面的可预见性和耐挫能力并不是很成熟,从而形成困难。
在实际的教学过程中,我们要引导学生先观察并思考网格中正方形的面积关系,再把这种关系转换成边长的关系,这样就可以让学生顺利成章地发现并证明勾股定理。但是,从网格中的等腰直角三角形,过渡到网格中的特殊的直角三角形,提出合理的猜想,这一步骤,学生有较大的困难,学生第一次通过构造图形的方法来解决定理的证明存在较大的难度,需要利用合理的割补方法求面积。八年级的学生虽然初步具有基本的几何意识,但是对勾股定理的探究— —证明— —应用,每一个环节都还存在一定的难点。
知识与技能:
1.了解勾股定理的历史背景,体验勾股定理的探索过程.
2.了解勾股定理的证明方法.
3.勾股定理的简单运用.
过程与方法:
1.在探索勾股定理的过程中体会和发展观察—猜想—归纳—证明的合情推理方式.
2.体会数形结合、从特殊到一般的数学思想、转化与划归思想,在应用中体会从一般到特殊的数学思想。
情感态度与价值观:
1.通过了解勾股定理的历史背景,体会其文化价值,从而获得文化自信.
2.通过探究活动,体会解决问题的方法的多样性,培养合作交流意识和探索精神.
教学重点:
1.勾股定理的探索与验证.
2.运用勾股定理进行计算.
教学难点:
用面积法来证明勾股定理,体会数形结合的思想.


师:亲爱的同学们,你们听说过勾股定理吗?
师:相信同学们对这个鼎鼎大名的定理早就有所耳闻了,但是你们知道它是怎么被发现的吗?它又为何叫做勾股定理呢?
一切都可追溯到公元前十一世纪,也就是西周时期,数学家商高与周公论道时就曾提到“勾三股四弦五”这样一组经典的勾股数。相传在公元前3世纪,古希腊大数学家毕达哥拉斯有一回在朋友家做客时,低头看地板砖也看出了隐藏其中的勾股定理。接下来,就让我们穿越到2500年前,跟随毕达哥拉斯来到他朋友家的地板前,一起来对勾股定理一探究竟吧。(板书课题:勾股定理 第1课时)
【师生活动】
师:引入勾股定理。
生:感受情境。
【设计意图】
通过史实的引入,调动学生的学习兴趣。让学生感受到数学来源于生活,与我们息息相关。
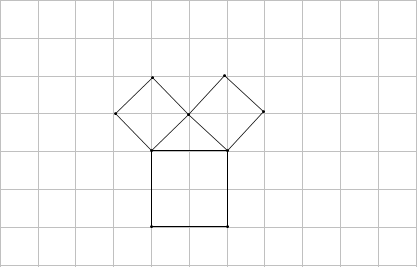
1、 师:地板是由哪一种最基本的图形构成的呢?
生:等腰直角三角形
师:以等腰直角三角形的三边为边长分别作三个正方形,那么这三个正方形的面积有什么关系?
生:以两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积。
师:若将这三个正方形如图所示分别记为、
、
,则面积关系可以表示为什么?
生:可表示为:
师:等腰直角三角形的三边之间有什么关系?
生:两直角边的平方和等于斜边的平方。
师:如果将等腰直角三角形的三边记为、
、
则三边关系可以表示为什么?
生:可表示为:
2、师:等腰直角三角形有这样的性质,其他的直角三角形也会有这样的性质吗?请同学们分别计算出图1、图2中正方形、
、
的面积,填写表格。
(割补法求C的面积)
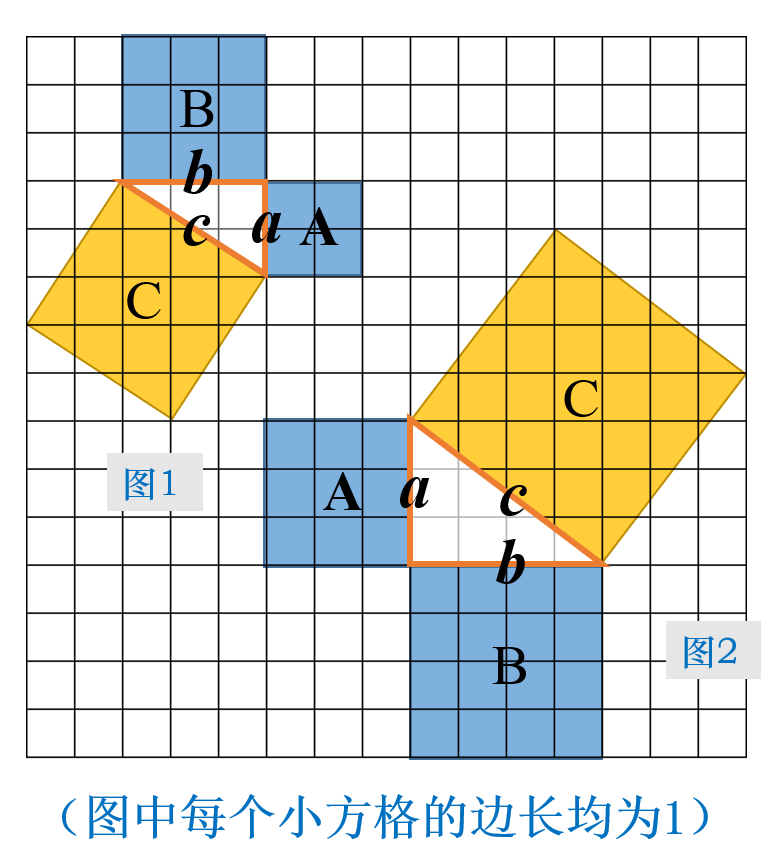
|
|
| |
图1 | |||
图2 | |||
正方形 | |||
师:根据刚刚的探索,你能猜想:一般直角三角形的三边之间有怎样的关系吗?
师板书:
猜想:如果直角三角形的两直角边长分别为,
,斜边长为
,那么
.
3、师:这只是猜想,到底对不对呢?接下来,就让老师变身我国汉代数学家赵爽,展示他的证明方法,一起来领略古人的智慧吧。
老师利用实现准备好的双层磁性纸,展示赵爽证明勾股定理的过程。
赵爽通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理,实在是太高明了。顺便一提,赵爽弦图被选为了2002年在北京召开的国际数学家大会的会徽。
4、师:见识了古代数学家赵爽的证明方法,接下来该我们自己大显身手啦,只要敢想敢试,我们也可以是大数学家!
请用同学们用4个全等的直角三角形拼出一个以斜边为边长的正方形。小组之间交流合作,看哪个组拼得最快。
请两个小组分别展示两种不同的拼图方法,并贴到黑板上。
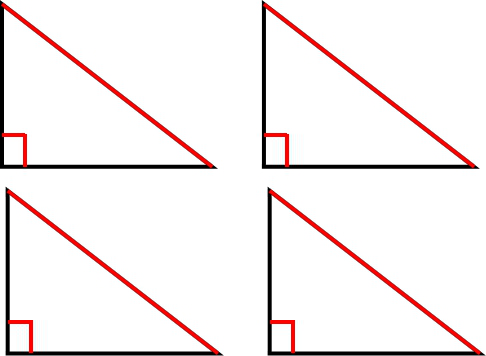

师:我们手中的四个直角三角形的两直角边为,
,斜边长为
,,你能用不同的方法来表示拼出的这个边长为
的正方形的面积吗?
图1:老师请学生回答,顺势推导,学生能推出更佳。
图2:学生独立完成。并上台板演推导过程。
师:欣赏更多历史上的证明方法(播放微视频)
师:猜想经过这么多方法的证明,已经真的不能再真了,于是它就变成了定理。
请同学像老师一样将手臂弯成一个直角,我国古代学者将较短的小臂称为“勾”,较长的大臂称为“股”,拳头与肩膀的连线段称为“弦”,因此这个定理在我国称之为勾股定理。在国外,因为是毕达哥拉斯发现的,故又被称为毕达哥拉斯定理。
定理:如果直角三角形的两直角边长分别为,
,斜边长为
,那么
.
师强调:只适用于直角三角形、直角所对的边是斜边、文字表述为:两直角边的平方和等于斜边的平方。
【师生活动】
师:处处留心皆学问,看似平淡无奇的现象却蕴含着深刻的道理。从毕达哥拉斯的这一发现,你能体会怎样的数学思想?
生:归纳说明这一发现体现的数学思想方法。
师:这一发现也充分体现了数学来源于生活。
师:毕达哥拉斯的这一发现是建立在等腰直角三角形的前提上,如果只是一个直角三角形,还有同样的结论吗?能否推广到一般的直角三角形?
生:完成小组合作探究。
【设计意图】
通过小组探究,体会从一般到特殊的这一探索问题的方法,从而了解定理的发现过程。
通过拼图活动,将抽象的问题形象化,使学生更直观地理解定理,体会数学中的数形结合思想。通过自主证明,增强学生学习数学的信心。
通过对我国关于勾股定理的数学史的介绍,让学生充分了解我国古代数学家对勾股定理的发现与证明做出的贡献,增强民族自豪感和文化自信。
师既然已经得到了勾股定理,接下来就让我们大展拳脚,利用勾股定理解决问题。
例1.设直角三角形的两条直角边长分别为和
,斜边长为
. 已知
=6,
=10,求
;
(师讲解板书示范)
练习 设直角三角形的两条直角边长分别为和
,斜边长为
.
(1) 已知=5,
=12,求
;
(2) 已知=25,
=15,求
.
变式1 在一个直角三角形中, 两边长分别为6和8,求第三边的长.(分类讨论思想)
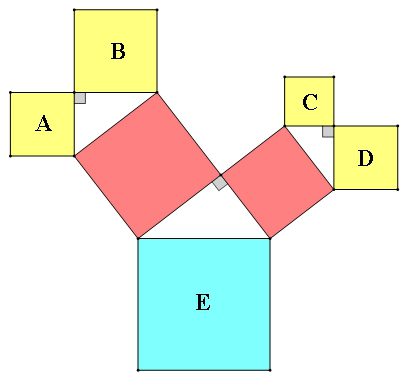
例2.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形,
,
,
的面积分别是12 ,16,9,12,则最大正方形E的面积是_________.
【师生活动】
老师讲解板书例题,学生完成练习与变式。
【设计意图】
通过勾股定理的学习理解定理的具体内容,从而了解定理的具体要求及使用方向,对定理的灵活运用打下基础。
本节课你有什么收获?又还有什么疑惑?
1.勾股定理
如果直角三角形的两直角边长分别为,
斜边长为
,那么
.
2.勾股定理的应用
强调在一个直角三角形中,注意字母的含义。
3.重要思想方法
从特殊到一般,从一般到特殊,数形结合,转化与化归,分类讨论
【师生活动】师:我们对于本堂课的收获或疑惑。
生:自我总结及反思
【设计意图】
通过课堂小结,回顾本节课的内容,再一次熟练勾股定理的内容,加强理解。通过疑惑的提出,反思自己对所学知识的理解程度及时补全知识漏洞。
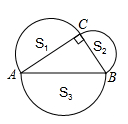
1.如图,∠=90°;,图中有阴影的三个半圆的面积有什么关系?
【师生活动】
师:老师提出一些疑惑。毕达哥拉斯是在一些正方形的地砖上发现的勾股定理,如果把正方形换成圆形呢,你还能得到什么样的结论?
生:完成拓展题2个。
【设计意图】
通过拓展提升,将所学知识进行迁移,不单可以联系勾股定理而且可以让学生学会探索发现规律性结论。
设为正确答案