- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节教材安排了对勾股定理的观察、计算、猜想、证明及简单的应用的过程。在勾股定理的探求过程中蕴含了丰富的数学思想,把直角三角形有一个直角的“形”的特点转化为三边之间的“数”的关系,体现了数形结合思想和转化思想;先探求特殊的直角三角形的三边关系,再探求一般的直角三角形的三边关系,体现了从特殊到一般的思想。
在本节课之前,学生已经学习了有关三角形的一些知识,也经历了通过图形面积来探求数式运算规律的过程。本节课,教师通过提供活动方案,让学生经历“观察——猜想——归纳——验证”以及动手操作等探究过程,学生能主动构建新的知识网络,理解面积法搭起了勾股定理从形到数的桥梁。
知识与能力:1.了解勾股定理的文化背景,体验勾股定理的探索过程。2.在勾股定理的探求过程中,发展合情推理能力,体会数形结合思想。
过程与方法:1.让学生经历“观察——猜想——归纳——验证”的数学过程,体会数形结合思想和由特殊到一般的思想方法。2.通过数学活动,体验数学思维的严谨性,发展形象思维。在探究活动中,学会与人合作并与他人交流思维的过程和探究的结果。
情感态度与价值观:1.在探索勾股定理的过程中,让学生体验解决问题的多样性,培养学生合作交流意识的探索精神;通过获得成功的体验和克服困难的经历,增进学生学习的信心。2.使学生在定理探索过程中,感受数学之美,探究之趣。3.在数学活动中,使学生了解勾股定理的历史,感受数学文化,激发学习热情,增强民族自豪感。
重点:探索、证明勾股定理及勾股定理的简单应用。
难点:勾股定理的探索与证明。
17.1 勾股定理
1.定理:如图,在Rt△ABC中,a2+b2=c2. 公式变形:
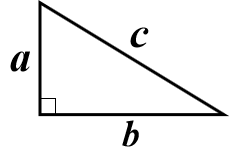
2.方法:割补法,等面积法
习题板书
3.思想:转化、方程、分类思想
【教师提问】
今天,建豪跑过来跟我说:”金老师,我知道今天要学习什么内容。“,我说:”你说说看.“,说着,他摆出了如图所示的造型,同学们,你知道这个造型的含义吗?

【教师衔接】
相传2500年前,古希腊有一位非常著名的数学家毕达哥拉斯,他善于观察和思考问题,经常从生活中寻找一些数学问题,有一次,他到朋友家做客,发现朋友家的用砖铺成的地面中反映了一个神奇的数学现象.

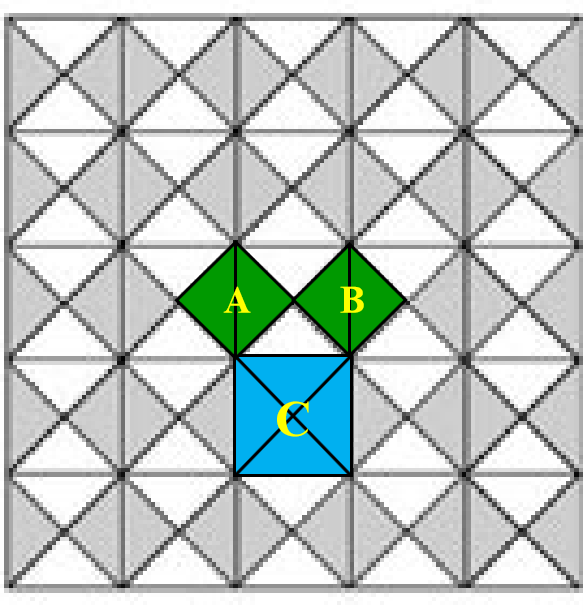
【教师提问】
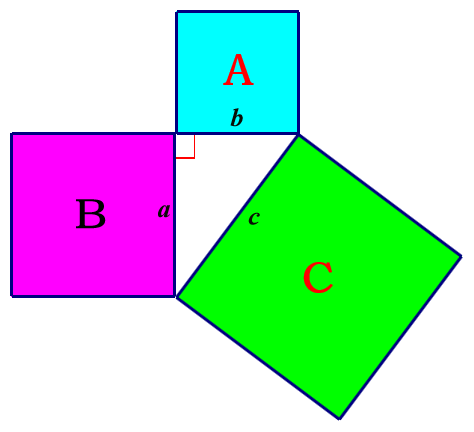
如图,分别以直角三角形的三边为边向外作正方形A、B、C,则正方形A、B、C的面积之间有何关系?
【学生回答】
正方形A、B的面积之和等于正方形C的面积.
【教师操作】
为例举更多情况,我们借助几何画板工具(教师打开几何画板超链接),请大家观察在改变直角三角形的形状和大小后,正方形A、B、C的面积之间有何关系?
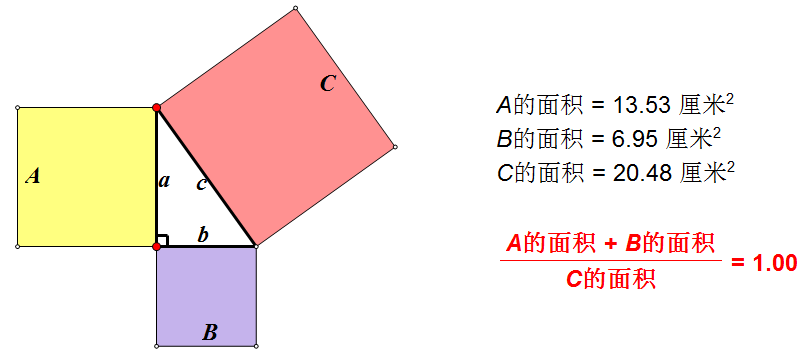
【教师提问】
由此我们得到什么猜想?
【学生猜想】
如图,如果直角三角形的两直角边长分别为a、b,斜边为c,那么a2+b2=c2.
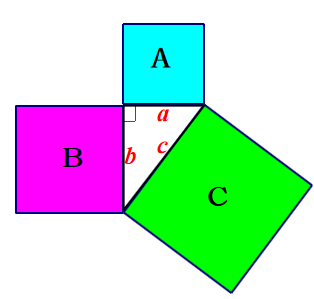
【教师提问】
你知道如何严谨证明吗?
与之类似的等式中,我们以前已经学了完全平方公式和平方差公式,大家一起来回顾一下这两个公式的证法。
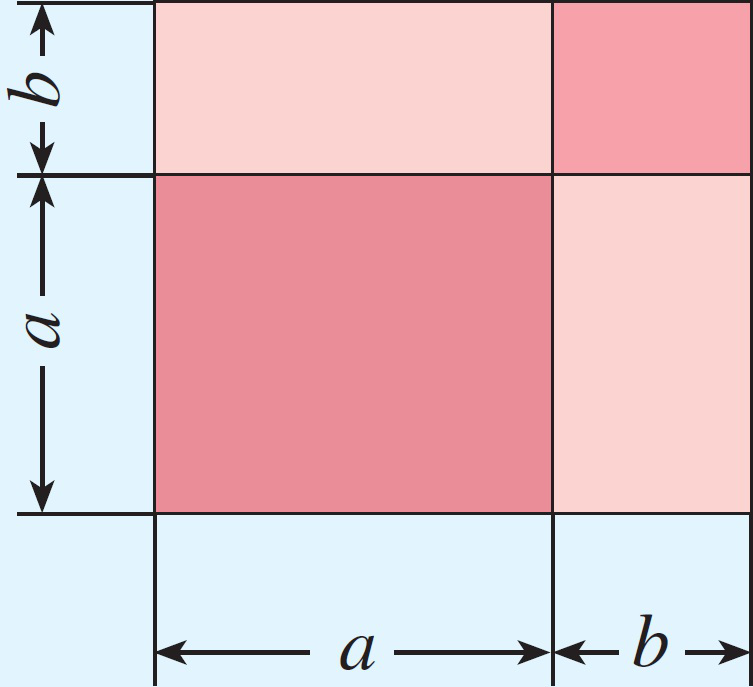
【教师提问】
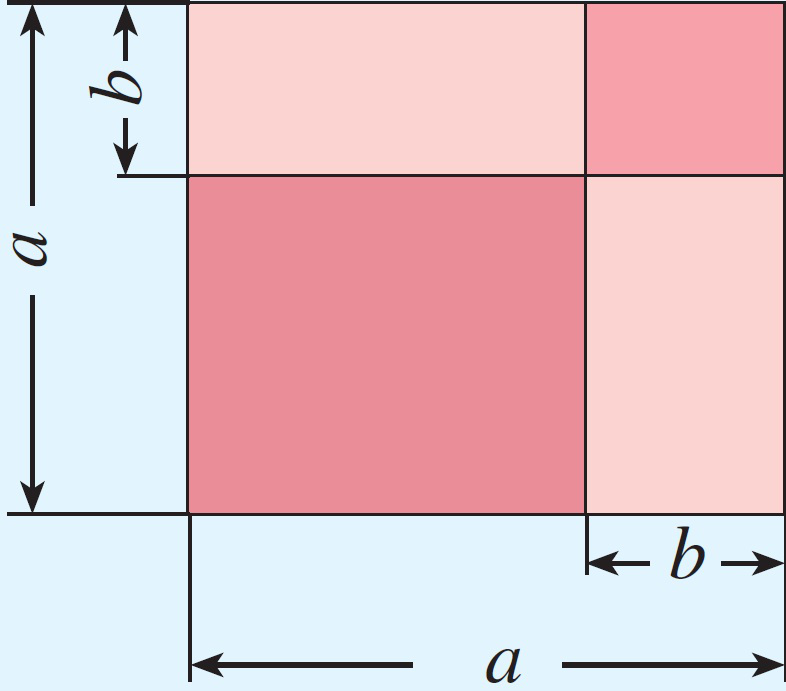
类比上述割补法,尝试利用下图证明a2+b2=c2.(一段时间后,若发现学生有一定困难,可适度提示或让其进行讨论.)
![]()
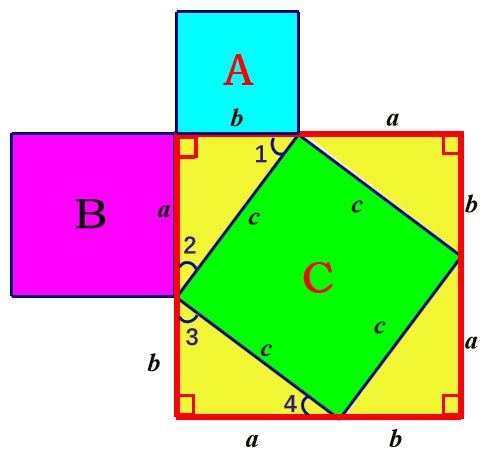
【学生讲解】
如图,将正方形C补成红色的大正方形.易证四个黄色的三角形全等,从而得到图中所有直角三角形的边长.而后将红色大正方形的面积用两种不同的方式表示,即:
(a+b)2=c2+4×0.5ab
∴ a2+b2=c2.
【教师提问】
在此证明过程中,体现了什么数学思想和方法?
【学生回答】
转化思想、割补法、等面积法.
如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.

即:直角三角形两直角边的平方和等于斜边的平方.
大家知道勾股定理共有多少种证法吗?约400.下面,让我们一起来欣赏其中有代表性的一些证法.
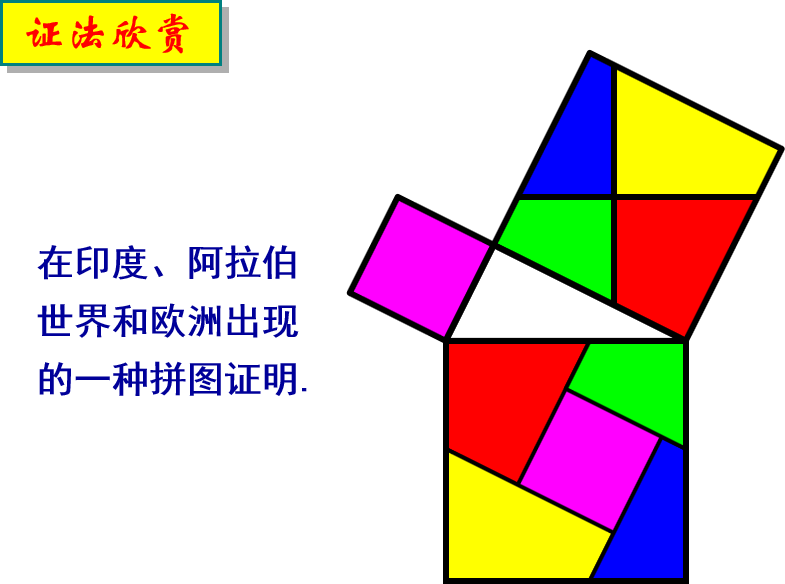
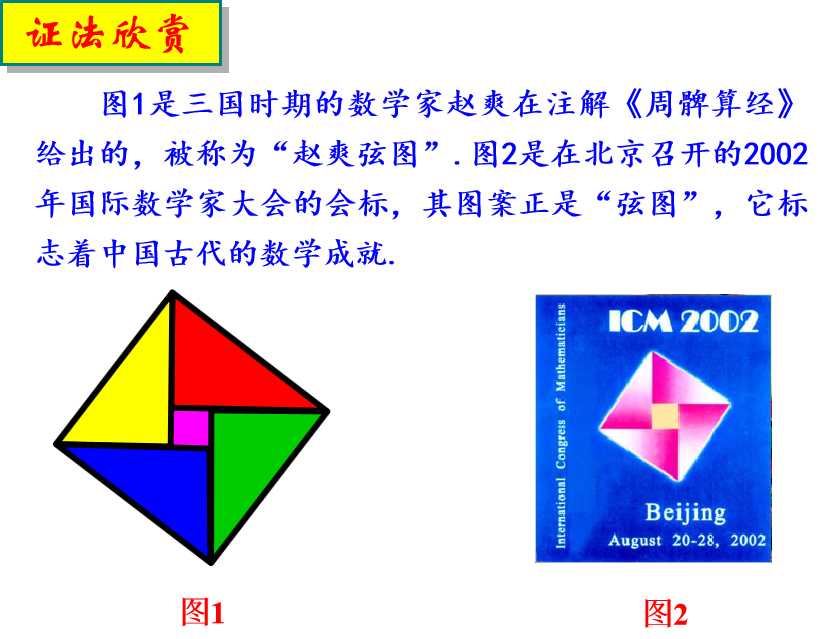
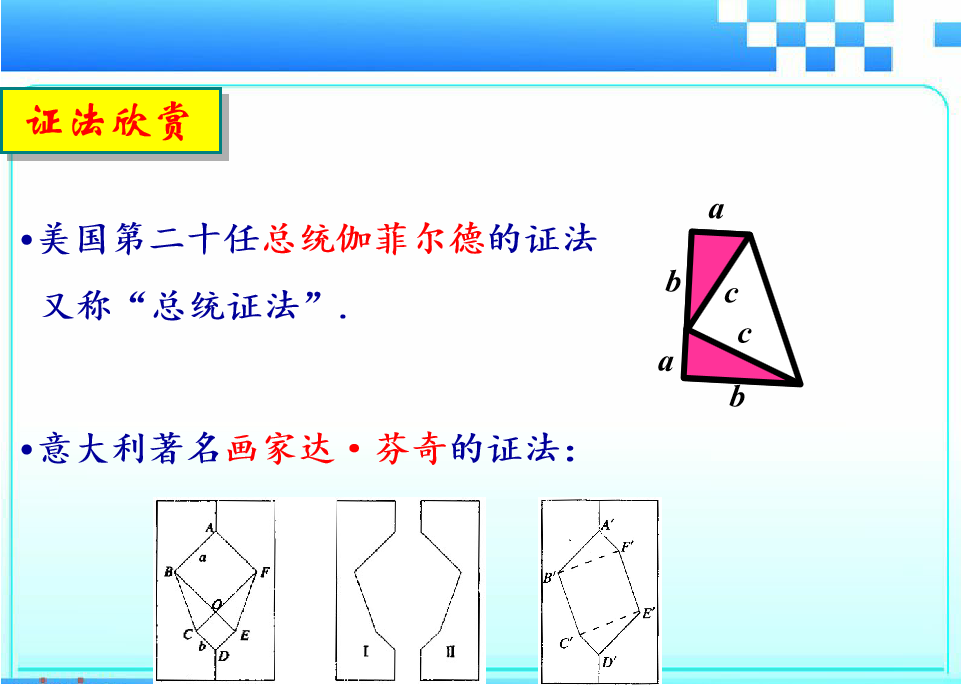
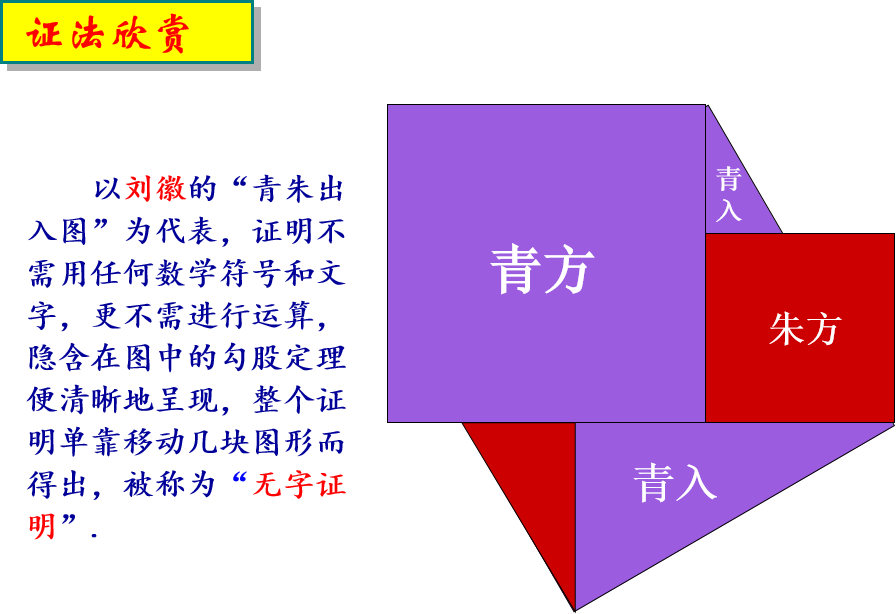
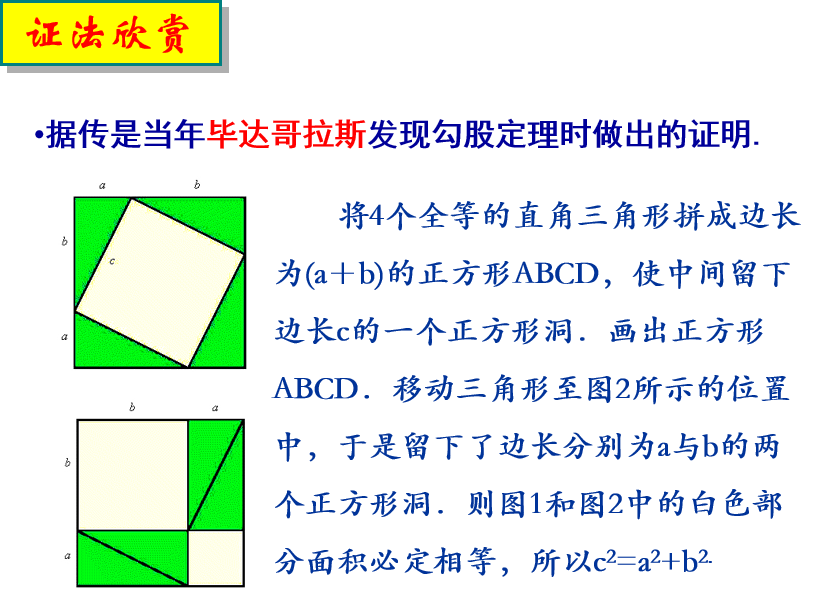
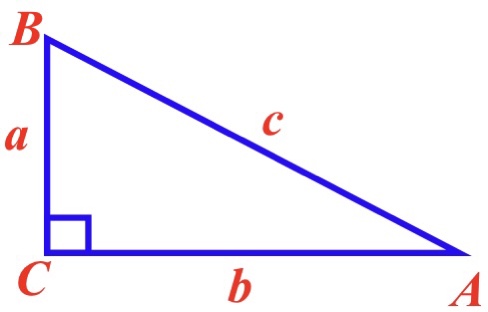
已知:如图,在Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= 13 ;
②若c = 6,b = 4,则a= ;
③若c = 25 ,a = 24 ,则b= 7 .
变式:④若 c= 10, a :b = 3 :4 , 则 a = 6 , b= 8 .(方程思想)
⑤若 c= 10, , 则 a = , b= .
变式④是从边的角度给条件,你能从其它角度出发添加一个条件,并求出a、b的值吗?
⑥若一个直角三角形的三边长分别为8,15, x,则x=_____________.(分类讨论思想)
【当堂测评】
利用平板测试功能当堂测评,并根据实际情况讲解.

【教师提问】
(1)这节课你学到了什么知识?
(2)你有哪方面的感悟?
(3)你还有哪些疑惑呢?
【课堂小结】
1.一个定理(勾股定理)
2.两个方法(割补法、等面积法)
3.三个思想(转化思想、方程思想、分类思想)
【课后作业】
(1)教材P241,2(必做).
(2) 根据下图证明勾股定理(必做).
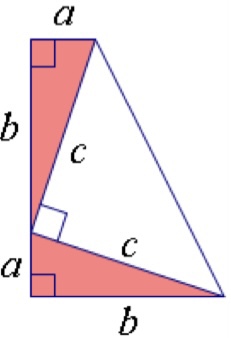
(3)通过查阅资料、上网,阅读了解更多有关勾股定理的历史和证明方法(选做).
设为正确答案