- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



有关无理数的知识是湘教版八年级上第三章的内容,隶属于“数与代数”领域,教材中第一次出现无理数的概念是在第三章第一节第二课时。本节课在学习了平方根的概念的基础上安排的,从开不尽方的谈起,将学生对数的认知在有理数的基础上,引入无理数,同时为后面学习实数及二次根式做铺垫,也是后期学习一元二次方程,解三角形的基础。本着从学生实际认知情况出发,从拼图游戏出发,引入课堂,从求面积为2的正方形的边长出发,自然引入
,在自主合作探究交流的过程中,观察、分析、归纳、概括的基础上,理解无理数的概念,抓住本质,帮助学生理解有理数和无理数的区别,能够辨别有理数和无理数并理解无理数的三种表现形式。
教学对象是八年级学生,
从学习内容的角度看,这是3.1平方根的第二课时,在学习本节课之前学生已经学习过有理数的概念及分类,初步认识了平方根,能求出一些平方数的平方根和算术平方根,知道了正数的平方根可以表示为“
”,其中算术平方根为
。这样就使得学生在探究活动中能自然得出
。
从认知的角度来看,八年级的学生已经逐渐能从具体事例中归纳问题本质,通过观察、类比等活动抽象出问题的规律,具有一定的分类思想;
从学习能力方面看,在前面的学习过程中,积累了自主合作探究的经验,具备合作交流和归纳概括能力。
1、知识与能力目标:
(1)发现无理数,了解数学史,得到无理数的概念;
(2)能够对所给数据进行分类,区分有理数,无理数;
(3)掌握初中阶段常见的无理数的三种表现形式。
2、过程与方法目标:
通过活动探索发现,在已有的有理数的基础上,难以解释一些问题,自然而然引入无理数,为实数的学习打下基础,为数域的扩充做准备。
3、情感态度与价值观目标:
(1)从拼图游戏中的的出现,再到对其进行估值,直观感受其不是有理数,进而引入无理数概念,再进一步对
是无理数进行证明,让学生感受知识发现,猜想,证明的全过程,有助于学生思维的发展,培养学生的数学核心素养。
(2)介绍无理数的发展历史,让学生感受无理数从无到有,从不完善到完善的产生,发展历程,从而体会到知识发展的艰辛和探索出错的正常,认识到在追求真理的道路上,坚持不懈才能有所成就,孜孜不倦终将克服困难,将数学教育与德育相结合。
教学重点
1、理解无理数概念;
2、能区分有理数,无理数;
3、引导学生总结归纳出无理数常见的三种表达形式。
教学难点
能区分有理数和无理数,并且按要求对数据进行分类。

活动一、情境导入,发现问题
拼图活动:上一节课结束就布置任务,给定两个边长为1的正方形,如何通过剪,拼,设法得到一个大正方形。请同学上来展示。
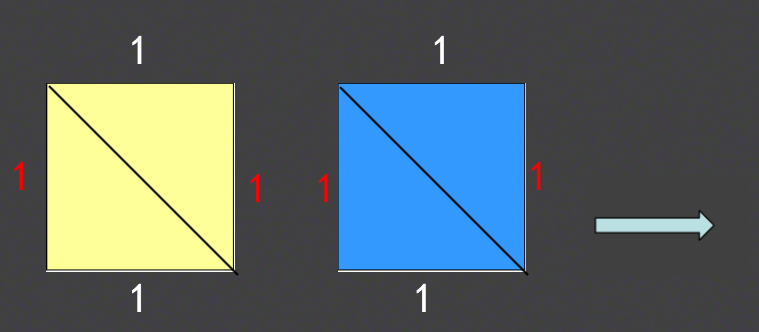
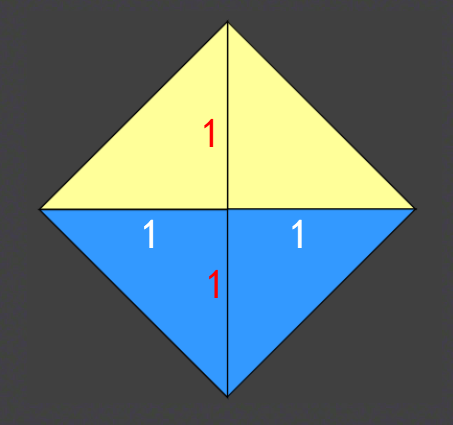
还会有其他一些展示:
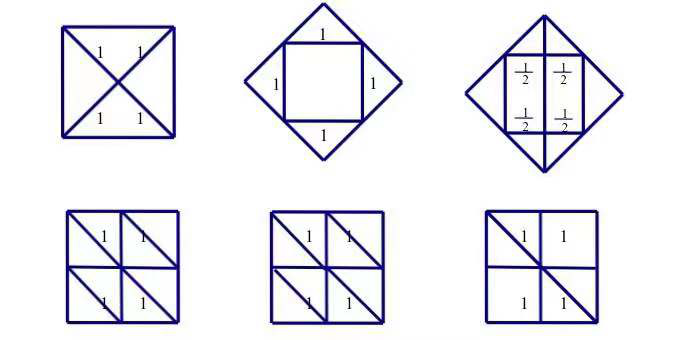
随即提出了问题串:
问题1:我们得到的这个新的大正方形的面积是多少?你能计算出它的边长吗?
设大正方形的边长为x,不难得出,根据实际意义和算术平方根的定义,我们可以得出
。
接下来,我们就从 谈起 吧!(观看数学史小视频,了解由
引发的第一次数学危机)
设计意图:
通过对无理数发现的小视频的观看,让学生了解数学史,丰富学生的视野,理解毕达哥拉斯学派,以及希帕索斯。让学生感受无理数从无到有,从不完善到完善的产生,发展历程,从而体会到知识发展的艰辛和探索出错的正常,认识到在追求真理的道路上,坚持不懈才能有所成就,孜孜不倦终将克服困难,将数学教育与德育相结合。
问题2:是整数吗?
很明显,不是整数,因为1的平方比2小,2的平方又比2大,所以
应该在1到2之间。
问题3:是分数吗?
1到2之间的分数有很多,其中有没有一个这样的分数,它平方以后恰好等于2?找几个分数试试看。
回忆旧知:
在之前,我们学习了有理数,知道了有理数包括整数和分数(也就是说,有理数可以写成两个整数的比的形式),而一般,分数可以可以写成有限小数和无限循环小数(无限循环小数可以化为分数并举例),有理数都可以写成两个整数之比,但我们刚直观发现感觉并不属于这两类。接着,我们来证明下
不是有理数。
活动二:证明不是有理数
其实早在2000多年前,古希腊数学家欧几里得就在《几何原本》中给出证明。采用反证法
证明,假设是有理数,则
可以写成两个互素的整数的比,设
,(
,
为正整数,且
,
互素)两边平方可得
,即
,
可发现等式右边是偶数,所以左边的也是偶数,可推出
是偶数,设
,则
,则
,同理,
也为偶数,这说明m,n有大于1的公约数,与假设矛盾。
现在我们已经严谨的证明了不是有理数,那么说明,我们的有理数不够用了,那就得用一种新的数来表示——无理数的产生。
设计意图:
通过复习有理数的分类和动手证明无限循环小数化分数,明白有理数的真正含义,为接下来证明不是有理数做准备,也能更好的理解无理数的含义。通过对
不是有理数的证明,发现确实有理数不够用了,让学生明白引入新的数——无理数是必须的。
活动三:探究的近似值
教师事先准备好数据:(这里可以考虑让学生自己用计算器进行计算,或者是教师用计算器展示,让学生感受不断逼近的过程)
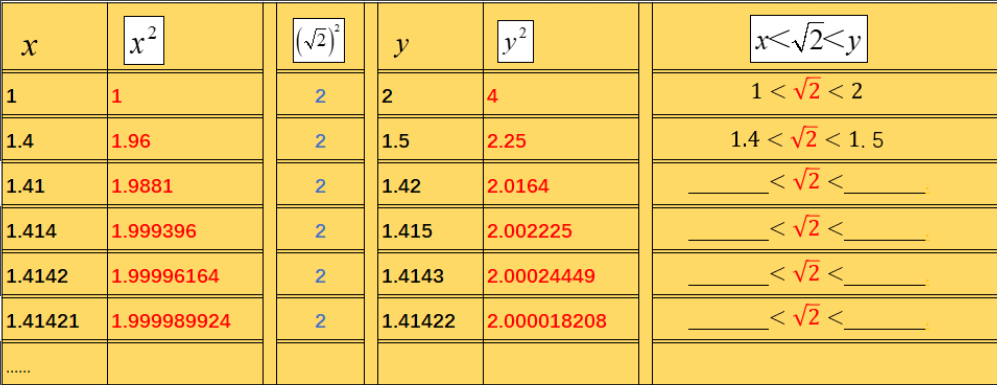
让学生直观感受是一个小数点后面的位数可以不断增加的小数,为无理数概念的引出埋下伏笔。
设计意图:
从拼图活动出发,让学生真实感受到的存在,通过问题串的设置,引导学生发现
不同于我们之前学过的整数和分数,用正方形面积对
近似值的探究,让学生直观感受
是无限不循环小数,体会无理数与有理数的区别。
我们已经证明了不是有理数,它是一个无限不循环小数。
无理数的概念:我们把无限不循环小数叫无理数。
注:我们之前学习过的也是无理数;
无理数也是有正负之分的;
根据实际的需要,我们往往用一个有限小数来近似表示一个无理数。
(此处可以让学生自己用计算器计算近似值)
设计意图:
总结对的探索,得出这一类数与有理数的区别,引入无理数的概念,并总结出初中常见的无理数的表现形式,加深学生对无理数的认识。
概念精致:
引导学生理解无理数的概念,抓住本质。让学生根据自己对无理数的理解,举例子,说出自认为是无理数的数,教师根据学生存在的问题,加以指点,师生共同总结出常见的无理数的表现形式。
师:大家学习了无理数的概念,大家能不能说出一些无理数?
生:.....
生:(有些学生异议),并且认为只要含有"根号”的数字就是无理数。
师:是无理数吗?我们知道
是有理数。
注1:并不是所有带根号的数都是无理数,只有开不尽方的数才是无理数。
师:除了开不尽方的数,你们还能举出其他无理数的例子?
生:老师,是无理数,那么,只要含
的数就是无理数吧。(部分学生异议)
生:不一定吧,比如,都是有理数。
注2:并不是所有含的数都是无理数。
师:那试卷上还会怎么表示无限不循环小数呢?比如0.1010010001...(每两个1之间0多一个),像这种有规律但无限不循环的人造数。各位同学也可尝试构造一些人造数。
总结归纳:

例题1.判断题(概念辨析)
①有理数都是有限小数。 ( )
②有限小数都是有理数。 ( )
③无理数都是无限小数。 ( )
④无限小数都是无理数。 ( )
⑤无理数都是开不尽方的数。 ( )
⑥开不尽方的数都是无理数。 ( )
⑦带根号的数都是无理数。 ( )
⑧无理数包括正无理数,0,负无理数。 ( )
例题2.(分类题)把下列各数进行分类,将它们填入相应位置:
有理数:
无理数:
例题3.(分类题)把下列各数进行分类,将它们填入相应位置:
正有理数: 正无理数:
负有理数: 负无理数:
设计意图:
通过学生自己的举例,帮助学生的练习,帮助学生更好地辨析无理数的概念,加深无理数的外延。同时,通过分类例题的练习,将之前学习过的一些运算综合在一起,形成知识网络。
问:本节课你学习了哪些知识?在探索知识的过程中,你用了哪些方法?
学生根据自己的学习情况进行概括总结,由学生举手发言,学生倾听同伴意见,互相补充。教师应关注学生的表现,包括知识掌握情况、情绪状况等,引导学生补充,共同概括。
这节课,我们一起感受了无理数的发现,发展历程,体会到了知识知识发展的艰辛和探索出错的正常。但是,在追求真理的道路上,我们坚信:坚持不懈才能有所成就,孜孜不倦终将克服困难。
学法大视野60--61页探究三
设为正确答案