- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课是普通高中课程标准实验教科书选择性必修第一册第三章《圆锥曲线的方程》中《椭圆》的第一节节选内容,主要学习椭圆的定义,它是本章也是整个解析几何部分的重要基础知识。
椭圆虽然是生产生活中常见的曲线,但对椭圆几何特征的探究与发现是个难点,因为很难由椭圆的形状想到椭圆的定义。为此,教材在用细绳画圆的基础上,通过分开细绳的两端,画出图形,归纳图形上点满足的几何条件:这个图形上的点到两个定点的距离和是定值。进而将具有这种几何特征的图形定义为椭圆。
教学时,应让学生认真观察画图的过程,抽象图形的几何特征,直观感知椭圆的形状。为后面学习椭圆的标准方程和几何性质做好铺垫。
在第二章《直线和圆的方程》的学习中,学生已经初步掌握了运用“坐标法”来研究几何问题.但是缺少主动通过方程蕴含的几何意义研究问题的意识。日常生活中,学生对椭圆的大致形状已经有了一定的感性认识,但并不清楚椭圆上的点满足的几何特征。
在学习本节课前,学生已经具备探究有关点的轨迹问题的知识基础和学习能力。教学中,要注意画图、抽象、归纳、概括的完整过程。让学生在充分讨论,用自己语言表述的基础上,给出准确、严谨的椭圆定义。另外本节内容蕴含了许多重要的数学思想方法,如:数形结合思想、类比思想、化归思想等。因此,教学时应重视体现数学的思想方法及价值。
(1)知识目标:掌握椭圆的定义;
(2)能力目标:学生通过动手画椭圆、分组讨论探究椭圆定义等过程,提高动手能力、合作学习能力和运用知识解决实际问题的能力。
(3)情感目标:在形成知识、提高能力的过程中,渗透数形结合的思想,启发学生研究问题时,抓住问题本质,严谨细致思考,培养学生勇于探索、敢于创新的科学精神。
教学重点:理解和掌握椭圆的定义。
教学难点:理解椭圆的定义中常数加以限制的原因。
一、画椭圆:
二、椭圆的定义:
三、例题剖析:
例1
例2
一、创设情境,实例引入
活动1:播放天问一号探测器的飞行轨道视频。
“天问一号”火星探测器成功发射,这一事件,再一次向世界表明,我们中国人有信心、有能力攀登一个又一个科学高峰。“天问一号”升空后,准确的进入预定轨道,它运行中期的轨道是一个椭圆。
活动2:举例生活中的椭圆形。
上至天文,地球的运行轨道是椭圆,探月卫星在飞向月球之前经历了多次椭圆轨道的飞行。下至百姓家庭,茶几的桌面可能是椭圆形的,菜碟也可能是椭圆形的。
在宇宙中还有许多天体的运行轨道也是椭圆,生活中也有许多椭圆形的实际例子。由此看来,若要探索浩瀚宇宙的奥秘,解决日常生活中与椭圆有关的一些实际问题,需要对椭圆这一图形进行研究。今天我们就来研究什么是椭圆及椭圆的标准方程。那么什么是椭圆呢?这节课我们一起来研究——椭圆的定义。
【设计意图】借助多媒体生动、直观的演示,使学生明确学习椭圆的重要性和必要性。多媒体动画展示 “天问一号”火星探测卫星的运行轨道,科普知识,激发学生爱国思想情怀,立德树人。引导学生用数学的眼光观察世界。通过欣赏生活中的椭圆,感受数学源于生活,激发学生进行研究椭圆的兴趣。同时激发他们探求实际问题的兴趣,使他们主动、积极地参与到教学中来,为后续的学习做好准备。
二、实验探究,归纳概念
(一) 合作探究,拉线作图
既然要研究椭圆,我们就应该先画一个椭圆。怎么画椭圆呢?
拜占庭数学家安提缪斯在研究燃烧镜时,给出了今天我们熟悉的椭圆的 “两钉一绳”画法(又称“园艺师画法”)。
指导学生互相合作(主要在于动手),体验画椭圆的过程(课前准备直尺、细绳、钉子、笔、纸板),并以此了解椭圆上的点的特征。
请三名同学在黑板上画。(注:在本环节中不急于向学生交待椭圆的定义,而是先设计一个实验,一来是为了给学生一个创造实验的机会,让学生体会椭圆上点的运动规律;二是通过实践,为进一步上升到理论做准备。)
画椭圆活动:
(1)取一条定长且没有弹性的细绳。
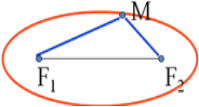
(2)在图纸上任取两点,将绳子的两端拉开一段距离, 把它的两端固定在两个定点F1、F2。
(3)用铅笔尖(P)把细绳拉紧,移动笔尖,看看笔尖画出的轨迹是什么曲线?
根据画图的过程,请同学们思考椭圆上的点有什么共同特征?
思考:在实验过程中,蕴含着哪些变化的关系,不变的关系?通过下面三个思考题让学生感受椭圆的形成过程中这些数量关系?逐步探寻到“定长”这一关系。
思考1:在实验的过程中,细绳的两端的位置是固定的还是运动的?
思考2:在实验的过程中,绳子的长度变了没有?
思考3:在实验的过程中,绳子的长度与两定点之间距离有怎样的大小关系?
【设计意图】以活动为载体,让学生在“做”中学数学,通过画圆、椭圆,给学生一个自己动手实验的机会;让学生经历知识的形成过程,积累感性经验,通过实践思考,为进一步上升到理论做准备,有助于培养学生严谨的科学精神,进一步提升学生的直观想象、数学抽象等核心素养.。
(二) 总结归纳,形成定义
请大家回想刚才的画图过程,使笔尖贴紧绳子且贴紧黑板(表明在同一平面内),绳长没有发生变化,这说明椭圆上每一点到两点的距离的和都相等,且都是绳长这一定值。又保证绳长大于| F1 F2|,这样就在平面内画出了椭圆,所有具有这些特征的点集在一起就形成了椭圆。
那下面你能类比圆的定义(平面内与定点的距离等于定长的点的轨迹叫圆)给出椭圆的定义吗?那么请同学们给椭圆下个定义吧!
1.椭圆的定义:平面内到两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫椭圆。
2.这两个定点F1、F2叫做椭圆的焦点,两焦点之间的距离叫做焦距.记为2c.
3.师生共同完善椭圆定义的集合语言:
4.概念的深化
思考:在定义中,如果没有的条件,动点的轨迹又是什么?
当时,点M的轨迹为:线段
当时,点M的轨迹不存在。
那你认为椭圆的定义中,我们需要注意哪几个关键词?
(1)平面--大前提;
(2)任意一点到两个定点的距离的和等于常数;
(3)常数大于焦距
.
【设计意图】借助几何直观,通过实验抽象出椭圆的定义,培养学生用数学语言描述世界的能力;在概念的理解上,体会运动变化、对立统一的思想。数学中的定义都具有充分必要性。通过学生亲自动手画椭圆,使学生找到椭圆概念的充分必要条件。结合几何画板演示,形象直观的说明定义中的必备条件,在变化的过程中培养学生用联系与发展的观点看问题。有助于培养学生严谨的科学精神,进一步提升学生的直观想象、数学抽象等核心素养, 体会数学的理性与严谨。
三、应用举例,及时评价
例1.用定义判断下列动点M的轨迹用是否为椭圆。
(1)到(-2,0)、
(2,0)的距离之和为6的点的轨迹。
(2)到(0,-2)、
(0,2)的距离之和为4的点的轨迹。
(3)到(-2,0)、
(2,0)的距离之和为3的点的轨迹。
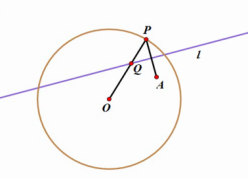
例2.如图,圆的半径为定长
,
是圆
内一个定点,
是圆上任意一点,线段
的垂直平分线
和直线
相交于点
,当点
在圆上运动时,点
的轨迹是什么?为什么?
【牛刀小试,及时巩固】
1.已知∆ABC的周长为16,则顶点C的运动轨迹是____.
2.与圆外切,且与圆
内切的动圆圆心P的轨迹是什么?为什么?
【设计意图】通过问题辨析加深对概念的理解,培养学生辩证思维能力。结合练习找到定义中的需注意的点,让学生通过自主思考,加深对椭圆定义的理解,培养学生用数学知识解析世界的能力。
四、课堂小结,加深理解
本节课学习的主要知识是什么?通过今天的学习,你有哪些收获?
椭圆的定义:平面内,与两个定点,
的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
【设计意图】进行课堂总结时,指导学生进行规律性知识与方法的归纳总结,通过“多面互动”,回顾经历知识的探究过程,体会与数形结合的数学思想。让学生自主建构、在动态中生成,从而培养学生的概括能力。并将所学知识纳入已有的认知结构。
【作业】
1、教材P115第10题;
2、预习椭圆的标准方程的推导;
设为正确答案