- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



为了解决生产,在日常生活中人们希望寻求最佳解决方案,从而产生了最短路径问题,也是我们本节课学习的重点。
本节课的主要内容是利用轴对称研究某些最短路径问题,初中阶段主要以“两点之间,线段最短”,“连接直线外一点与直线上各点的所有线段中,垂线段最短”“三角形两边之和大于第三边”,为理论基础,有时还要借助轴对称等变换进行研究。
本节课以数学史中的一个经典问题——“将军饮马问题”为载体开展对“最短路径问题”的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”问题。
引导学生从异侧问题转化成同侧问题,是本节课需要解决的重点。
八年级的学生直接经验少,理解能力差,抽象思维水平较低,处于直觉经验型思维向逻辑思维的过渡阶段,辩证思维还只是处在萌芽和初始的状态上。
由于八年级学生首次遇到某条线段和最小,而最短路径问题从本质上说是最值问题,作为初中生,在此前很少涉及最值问题,解决这方面问题的数学经验尚显不足,特别是面对具有实际背景的最值问题,更会感到陌生,无从下手。另外证明两条线段和最小时要选取另外一点,学生想不到、不会用,所以利用轴对称将最短路径问题转化为线段和最小问题,逻辑推理证明所求距离最短是本节课的难点。
对于直线异侧的两点,怎样在直线上找到一点,使这一点到这两点的距离之和最小,学生很容易想到连接这两点,所连线段与直线的交点就是所求的点。但对于直线同侧的两点,如何在直线上找到一点,使这一点到这两点的距离之和最小,一些学生会感到茫然,找不到解决问题的思路。
在证明“最短”时,需要在直线上任取一点(与所求作的点不重合),证明所连线段和大于所求作的线段和,学生想不到、不会用。
教学时,教师可从“直线异侧的两点”过渡到“直线同侧的两点”,为学生搭建“脚手架”。
本节课的教学难点是:如何利用轴对称将最短路径问题转化为线段和最小问题。
2018版《数学课程标准》中指出:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”随着现代信息技术的飞速发展,极大地推进了应用数学与数学应用的发展,使得数学几乎渗透到每一个科学领域和人们生活的方方面面。为了适应科学技术发展的需要和培养高质量、高层次科技人才,这也就导致数学建模变得越来越重要了。数学建模难度大、涉及面广,数学建模的教学本身是一个不断探索、不断创新、不断完善和提高的过程。新课标强调从生产、生活等实际问题出发,引导学生运用数学知识,去解决实际问题,培养应用意识与能力。因此,数学建模是初中数学的重要任务之一,它是培养学生应用数学的意识和能力的有效途径和强有力的教学手段。
本节课让学生借助所学知识和生活经验独立思考或与他人合作,经历发现问题和提出问题、分析问题和解决、验证问题的全过程,感悟数学各部分内容之间,数学与实际生活之间及其他学科的联系.激发学生学习数学的兴趣,加深对所学数学内容的理解,它既是轴对称、平移知识运用的延续,又能培养学生自行探究,学会思考,在知识与能力转化上起到桥梁作用。
基于以上分析,本节课的教学目标和重难点确定为:
【教学目标】
1、知识与技能:能利用轴对称解决简单的最短路径问题;能将实际问题中的元素抽象为数学中的“点”与“线”。
2、过程与方法:利用轴对称将线段和最小问题转化为“两点之间,线段最短”问题。
3、情感态度价值观:在探索最短路径的过程中,体会轴对称的“桥梁”作用,感悟“转化”作用。
【教学重点】
利用轴对称等变换将最短路径问题转化为“两点之间,线段最短”问题。
【教学难点】
如何利用轴对称将最短路径问题转化线段和最小问题。
【教学目标解析】
学生能将实际问题中的“地点”、“河”抽象为数学中的“点”“线”,把实际问题抽象为数学问题;能利用轴对称将线段和最小问题转化为“两点之间,线段最短”问题;能通过逻辑推理证明所求距离最短;在探索最短路径的过程中,体会轴对称的“桥梁”作用,感悟转化思想和数学建模。

(一)创设情景:
【诗歌欣赏】我们经过课前微课预习学习,探究了很有趣的将军饮马问题,并且得到了数学模型一,那么将军饮马问题还有其他的数学模型吗?我们一起来探究一下吧!
【学生活动】欣赏诗歌,寻找诗中藏着的数学问题,引发学生想探究其他将军饮马的数学模型兴趣。
【设计意图】从数学史上久负盛名的“将军饮马问题”引入,增加学生们的数学底蕴和诗歌欣赏能力,提高其人文思想。
(二)探究新知:
1、探究一:
问题:如图,将军从家A地出发,先去河边饮马,再去军营B地,到河边什么地方饮马可使他所走的路线全程最短?
【学生活动】学生思考并回答,如何将实际问题转化为数学问题的;小组讨论,作图并展示小组成果;反思自己的作法是否正确。
【设计意图】学生主动探索,充分发挥学生的主动性,展示多种方法,产生思维冲突,引发学生进一步探究的学习欲望。
2、解决问题:
(1)化未知为已知;
(2)化同侧为异侧;
【学生活动】利用轴对称将同侧线段和最短转化为异侧线段和最短问题,借助轴对称,把折线转化为线段的长来求解。
【设计意图】让学生进一步体会作法的正确性,提高逻辑思维能力。并让学生在反思的过程中,体会轴对称的作用,感悟转化思想,丰富数学活动经验。
3、作图探究二:一定直线,同侧两定点
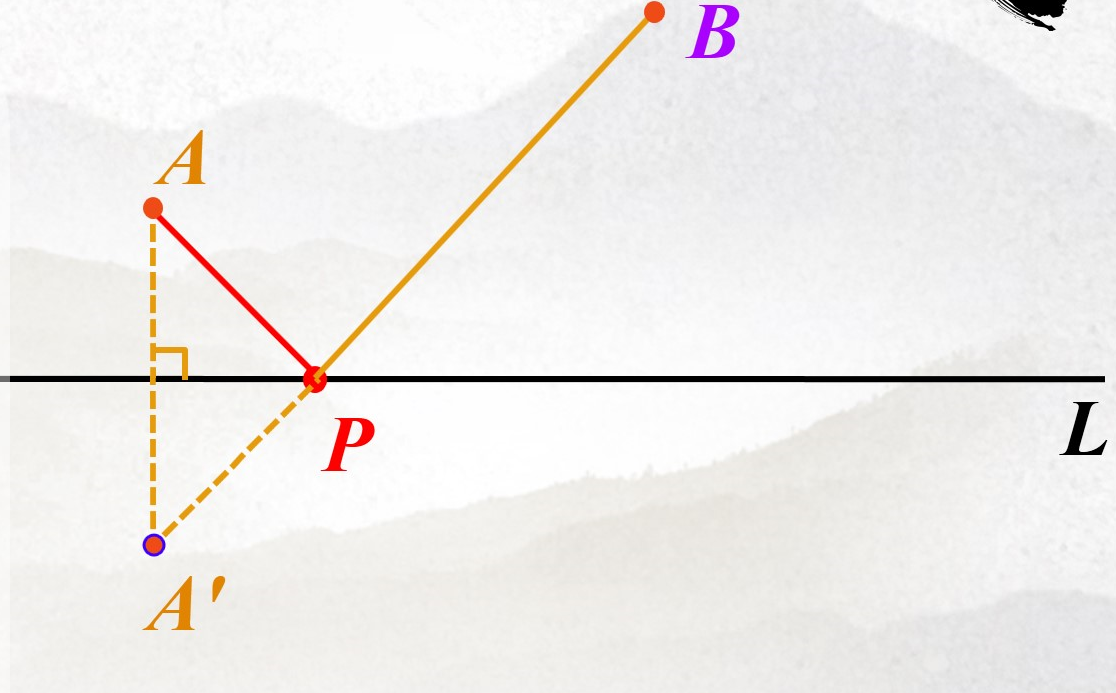
【学生活动】先通过学生对本题的思考尝试、并展示,师生共同纠错,提高认识与辩证思想,再通过老师的引导启发明白解决这个问题应该运用轴对称的性质。
【设计意图】教师一步一步引导学生,如何将同侧的两点转化为异侧的两点,为问题的解决提供思路,渗透转化思想。
4、探究三:问题验证
你能用所学的知识证明AP +BP最短吗?
证明:如图,在直线L上任取一点P′(与点P不重合),连接AP′,BP′,B′P′.由轴对称的性质知,
BP = ,BP′= .
∴ AP +BP= AP +B′P = AB′,
∴ AP′+BP′= .
在△AB′P′中,
AB′< ,
∴ <AP′+BP′.
即 最短.
【学生活动】认真观察、思考,要想确认AP+BP 最短,可以在直线L上任取一点P′(不与P重合)。
【设计意图】利用现代信息技术,通过移动点P的位置,可发现:当P′与P不重合时,AP+BP最短,当P′与P重合时,AP+BP=AP′+P′B,让学生很容易知道AP+BP最短,消除了学生的疑虑,发挥了多媒体的作用,让学生进一步体会作法的正确性,提高了逻辑思维能力。因为学生对几何语言的应用存在问题,所以我们研讨之后决定降低难度,从要求学生完全自己书写几何语言,到填空的形式。
5、视频讲解:同侧问题
【设计意图】引导学生梳理从实际问题抽象出来的数学模型。
(三)归纳总结:
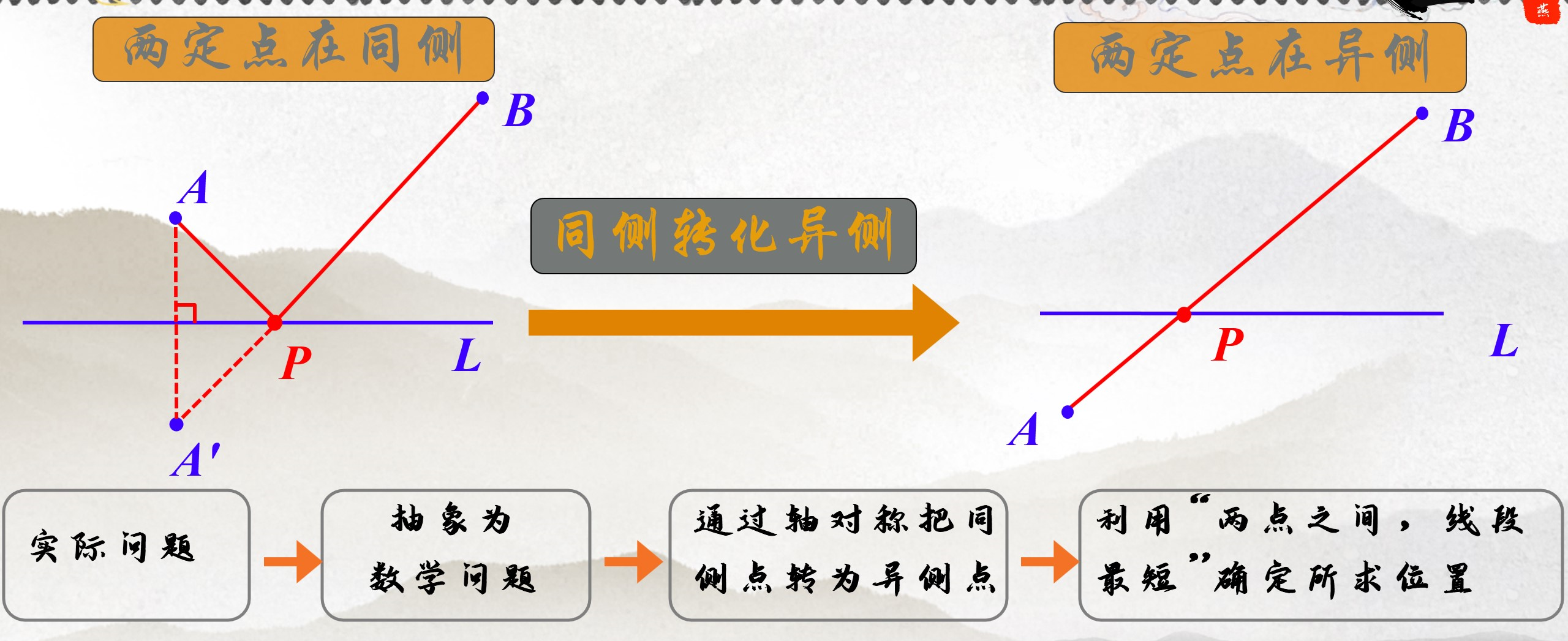
【设计意图】让学生在反思的过程中,体会轴对称的“桥梁”作用,感悟转化思想. 明确解题的方法与策略,为后面进一步的学习探究做准备。
(四)运用新知:

为了提升学生的趣味性,特增加一个幸运大转盘活动环节。
1、如图,直线L是一条河,P、Q是两个村庄.欲在L上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是—
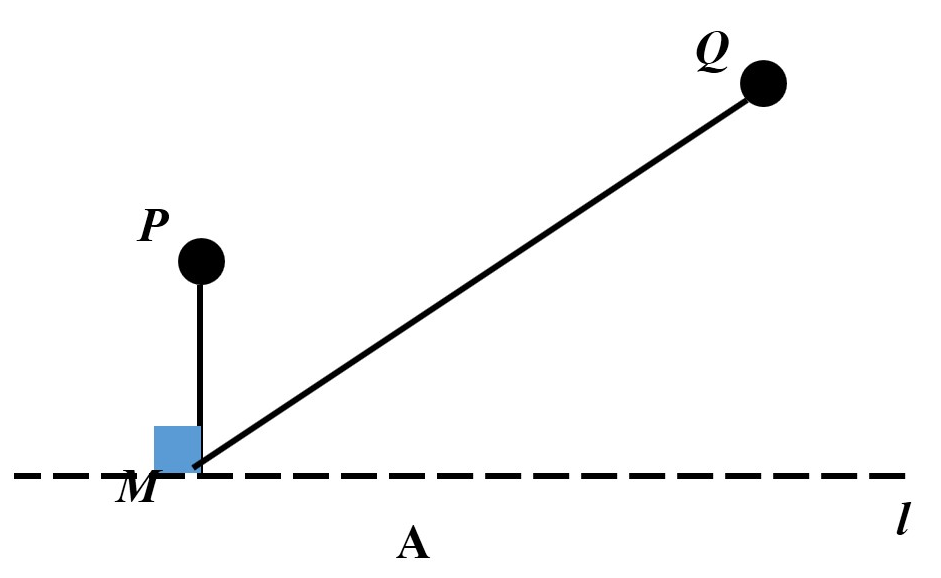
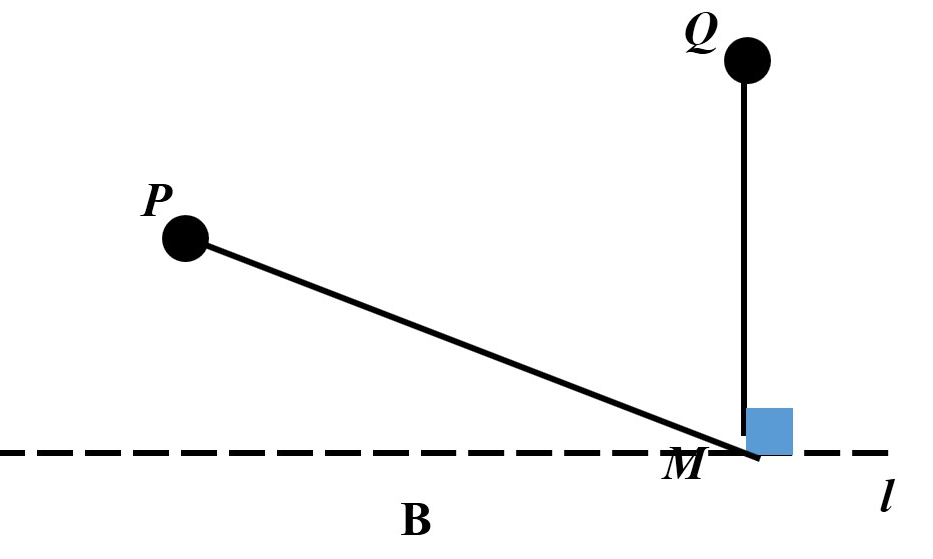
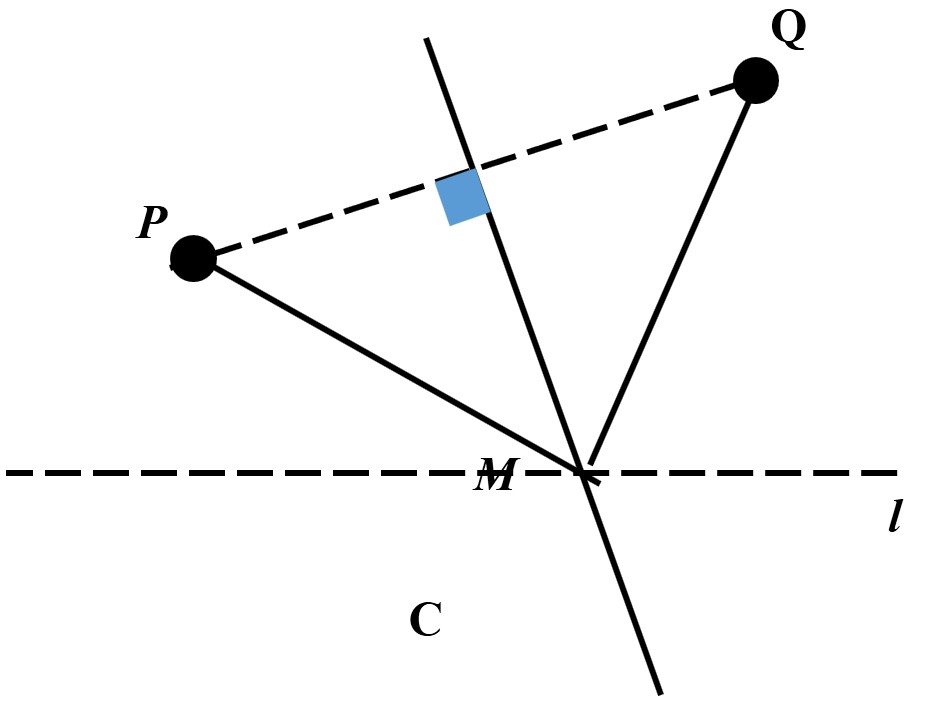
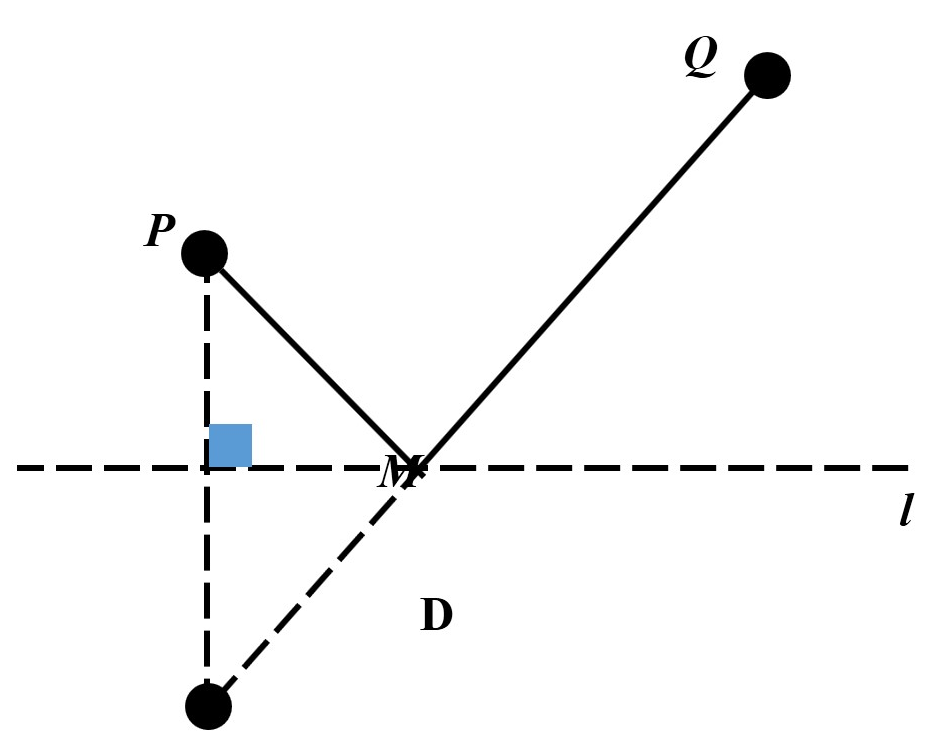
2、如图,牧童在A处放马,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把马牵到河边饮水再回家,所走的最短距离是( )米。

3、判断对错:
(1)实际问题不能转化成数学问题;
(2)同侧问题可以转化成异侧问题;
(3)两点之间,折线最短。
(4)求最短路径的思路可以使用化折为直的方法;
(5)将军饮马的求解思路可以利用轴对称;
【学生活动】利用习题让学生进一步巩固解决最短路径问题的基本策略和基本方法。
【设计意图】对前面所学的解题方法与思路得以巩固,让学生形成技能,进一步体会感悟数学中的转化思想,点学生上台操作演示,提高他们的学生兴趣与实践能力,体会成功的喜悦。以游戏的形式让学生对前面的内容进行复习,并且我利用了老师头像作为竞争人物头像,引起学生的兴趣能更认真的对待问题。
(六)课堂小结:
1、方法归纳:
为了让学生更好的观察二种数学模型的不同之处,特意利用超链接功能添加了放大镜功能。
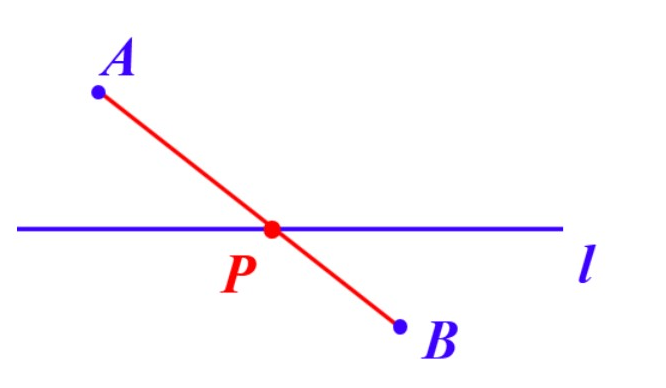
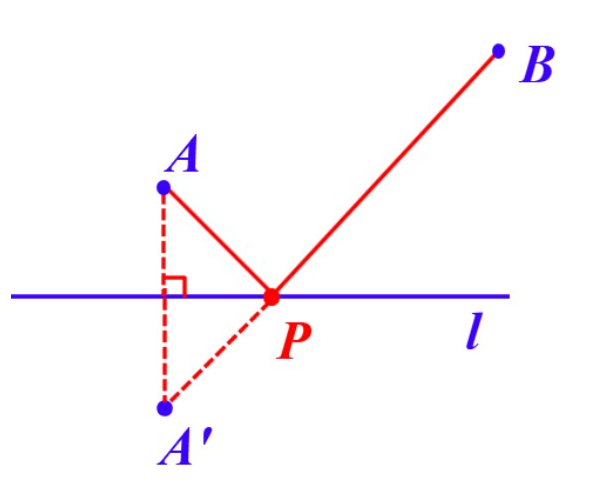
【设计意图】让学生加强对前面二种数学模型的认识,所以把二种数学模型集中进行展示,把数学模型的数学思维方法融入学生的思维当中。利用放大镜把每一个模型都单独呈现,这样可以加强学生的印象,然后再把四种模型集中一起呈现,可以更好的让学生观察四种模型的不同之处。
2、总结:将军饮马问题
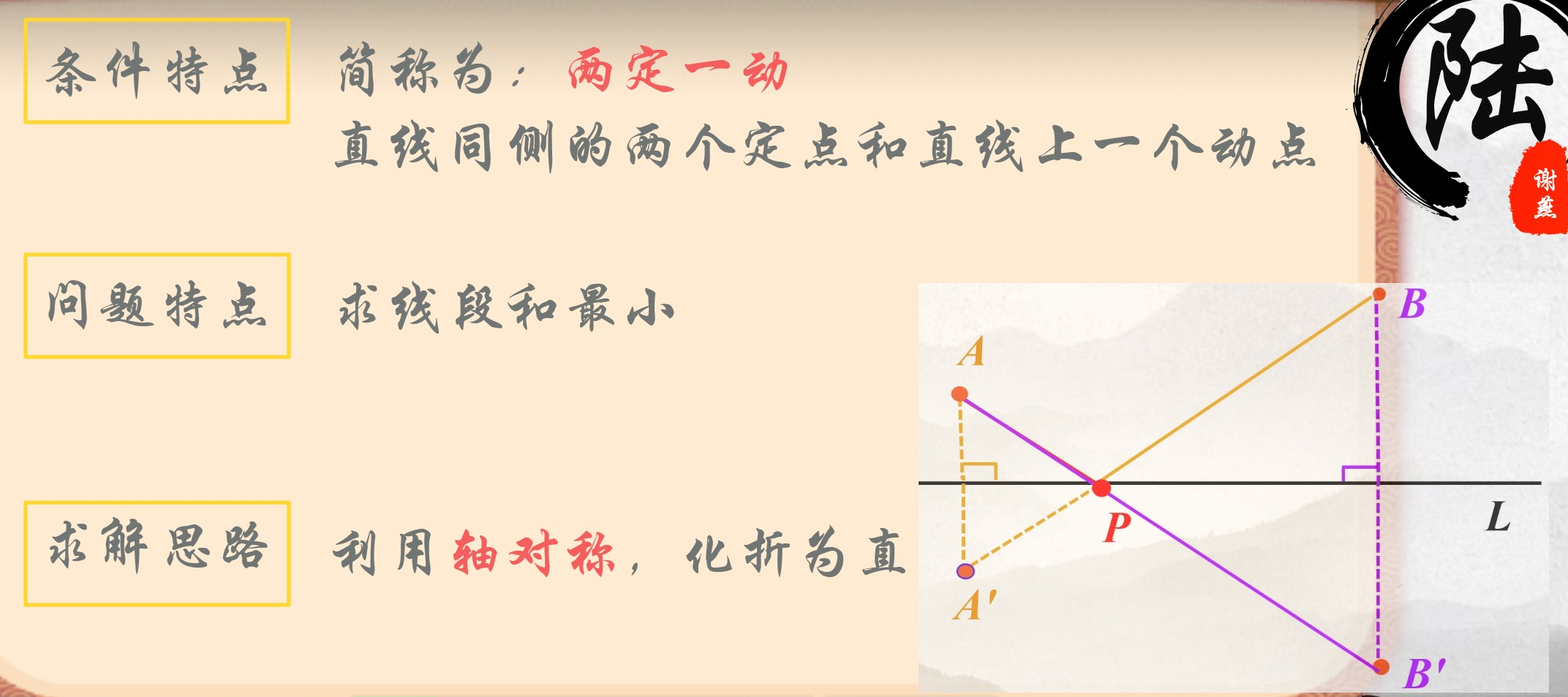
【设计意图】引导学生把握研究问题的基本策略和方法,体会轴对称在解决最短路径问题中的作用,感悟转化思想和数学模型的重要价值。
(七)布置作业:
1、必做题:课本P100,C组第18题。
2、思考题:你的梦想是什么?你认为实现梦想的最短路径是什么?
【设计意图】第一问考查学生解决“最短路径问题”的能力;第二个问题的设计,也是由课内向课外的一种延伸,预示着问题并没有终结,培养学生具有终身学习的意识与创新精神!
设为正确答案