- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习直线的倾斜角与斜率。直线是最常见的几何图形,在实际生活和生产中有广泛的应用。首先,初中几何对直线的基本性质作了比较系统的研究,初中代数研究了一次函数的图象和性质。本课内容是以上述知识为依据,在此基础上,对直线再进一步地认识和探讨。
直线的倾斜角与斜率是解析几何的重要概念之一,是刻画直线倾斜程度的几何要素与代数表示,是平面直角坐标系内以坐标法(解析法)的方式来研究直线及其几何性质(如直线的位置关系、交点坐标、点到直线的距离等)的基础。通过本节课的学习,能够培养学生观察、分析、猜想、抽象概括等数学基本思维方法,并初步体会坐标法的思想。
初中阶段,学生对直观图形仅仅停留在感性认识和简单的证明。进入高中选择性必修二的学习,第一章空间向量与立体几何对学生的空间想象能力和图形证明提出了更高的要求。第二章直线与方程更是数形结合思想的良好体现,而“直线的倾斜角和斜率”一节是解析几何的入门课。因此,从学生最熟悉的直线入手,以动画演示,去研究刻画直线的量——倾斜角与斜率。通过对这一问题的探索去揭示解析几何的本质是:用代数方法研究图形的几何性质。学生通过这一节的学习,初步感受数学研究的严谨性,生活问题的数学化、复杂问题简单化以及数形结合的思想重要性。
直线的倾斜角是本节课概念的基础,将为斜率的定义和公式推导打下铺垫。倾斜角和斜率二者之间的关系将是本节课的重点,斜率公式的推导是难点。对于推导“过两点的直线的斜率公式”要注意两个方面:(1)斜率的表象是纵坐标之差与横坐标之差的比值。学生理解这一表达式,将有利于后面直线位置关系的讨论和导数的概念等知识的学习;(2)斜率的本质与所取得点无关,即直线上的任意两点求出的斜率相等。
1、初步了解解析几何的产生及其意义,初步认识坐标法思想。
2、经历直线的倾斜角和斜率概念的抽象过程,理解直线的倾斜角和斜率的概念,发展数学抽象素养。
3、通过斜率公式的推导,掌握过两点的直线的斜率公式,提升逻辑推理、直观想象素养。
1、教学重点:理解直线倾斜角和斜率的概念及其关系。
2、教学难点:过两点的直线斜率的计算公式。

一、知识背景
在以往的几何学习中,我们常常通过直观感知、操作确认、思辨论证、度量计算等方法研究几何图形的形状、大小和位置关系,这种方法通常称为综合法.本章我们采用一种新的方法——坐标法研究几何图形的性质.坐标法是解析几何中最基本的研究方法。
解析几何是17世纪法国数学家笛卡儿和费马创立的,它的基本内涵和方法是:通过坐标系,把几何的基本元素——点和代数的基本对象——数(有序数对)对应起来,在此基础上建立曲线(点的轨迹)的方程,从而把几何问题转化为代数问题,通过代数方法研究几何图形的性质。我举个例子,同学们如果我问你,你家住在哪,最直接的方法是你可以带我去;你画张图告诉我,那类似几何方法;当然,一般你会告诉我,你家在哪,其实这就是一个坐标位置。这就是几何问题代数化最简单的生活实例。本节课就学习如何利用平面直角坐标系来研究直线的性质?
设计意图:通过介绍数学解析几何的知识背景,让学生了解平面直角坐标系。接着,通过举例让学生初步了解几何问题代数化的思想,最后提出问题“如何利用平面直角坐标系来研究直线的性质”,激发学生兴趣,引入今天的课题。
二、建模引入
播放一段冷水江市新城大桥的视频。


思考:冷水江新城大桥是娄底市首座规模最大的独塔斜拉桥,它的斜拉索的陡缓程度不一,我们如何建立恰当的数学模型来解释斜索的陡缓程度呢?
步骤一:建立一个直角坐标系,如何建最合理?
步骤二:在这个直角坐标系下,这些斜拉索可以看成什么?

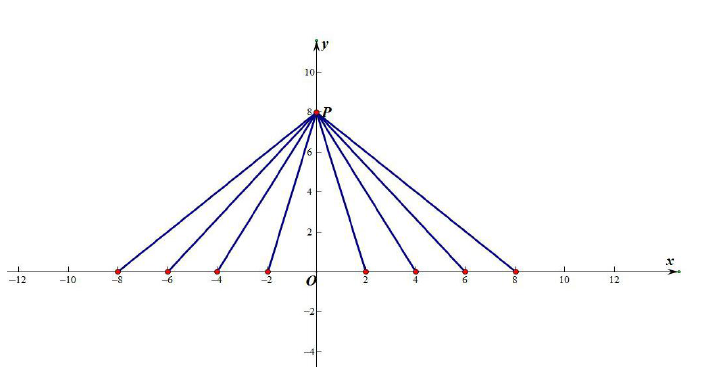
思考:这些斜拉索可以看成直角坐标系下的直线,这些直线有共同点与不同点呢?
提示:这些直线过同一点P,有的增有的减,有的增得很快,有的减得很慢等等,也就是说这些直线的方向不同,或者说是倾斜程度不同,那我们用什么来刻画直线的倾斜程度呢?
设计意图:活跃课堂氛围,也为新知的导出埋下伏笔。根据现实背景,建立斜拉桥的数学模型来解释斜索的陡缓程度,经历从现实问题中确定变量、探寻关系、建立模型的过程,形成和发展数学建模素养。
类比探究,用角来刻画直线的倾斜程度。
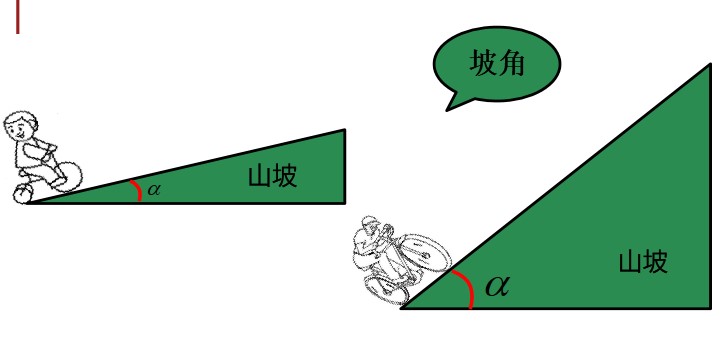
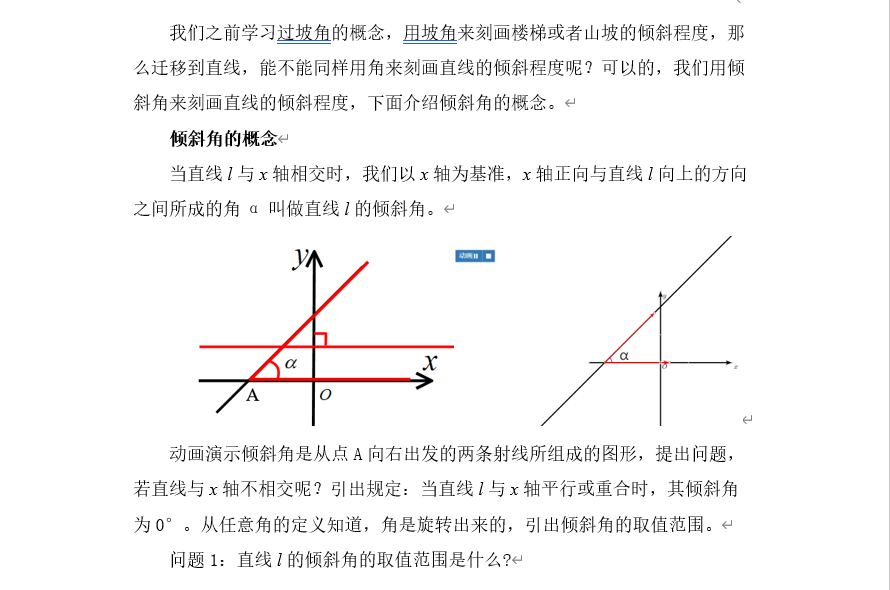
![]()
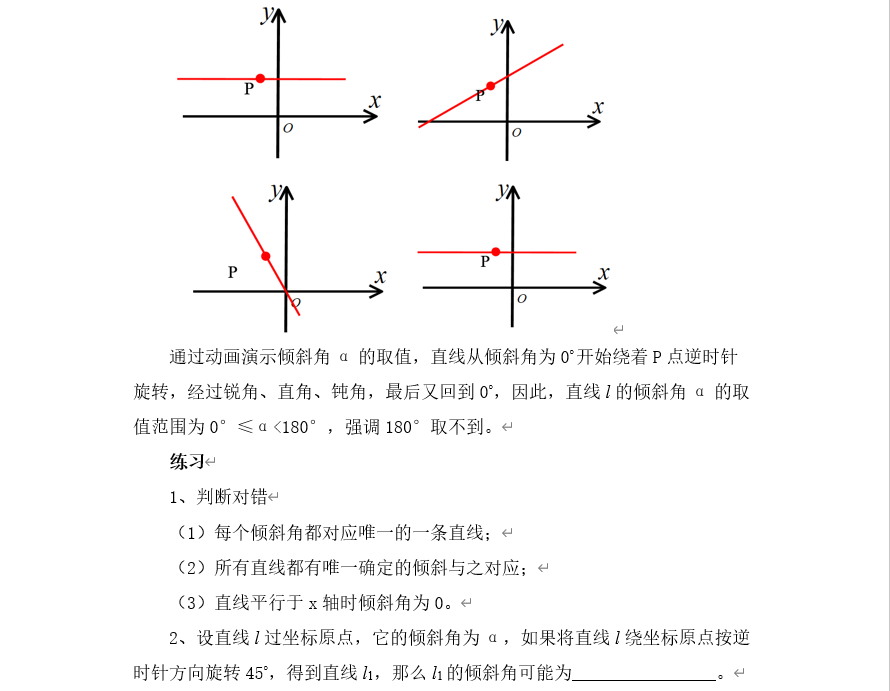
小结:平面直角坐标系中,每一条直线都有一个确定的倾斜角,而且方向相同的直线,其倾斜程度相同,倾斜角相等;方向不同的直线,其倾斜程度不同,倾斜角不相等。 因此,我们可以用倾斜角表示平面直角坐标系中一条直线的倾斜程度,也就表示了直线的方向。
确定平面直角坐标系内的一条直线位置几何要素是一个点和一个倾斜角。
设计意图:通过希沃白板的动画演示、画板演示、蒙层、思维导图、作业展示与批注、班级管理中随机点名、评价等技术手段完成这一知识点的教授任务。通过坡角知识的迁移,引出倾斜角的概念,对倾斜角的概念辨析到取值的分析,让学生了解倾斜角。
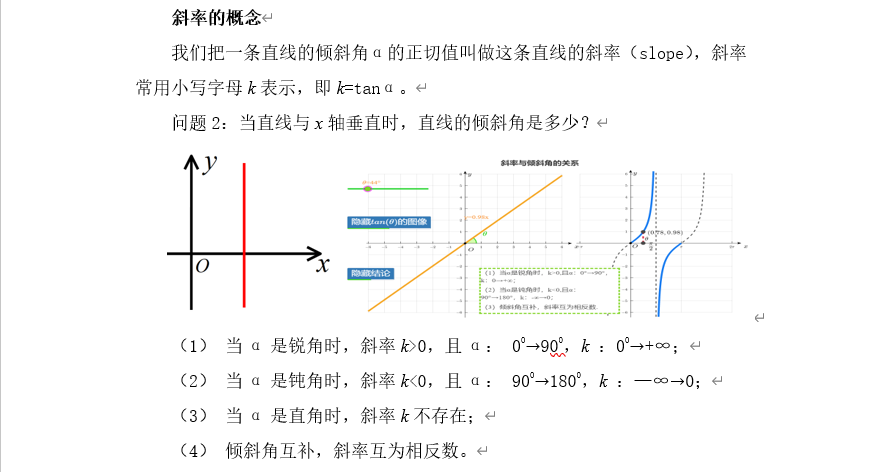
刚刚说的坡角的概念,是坡面与水平面的夹角,那么伴随坡角的还有一个坡度比的概念,坡度比=垂直高度/水平宽度,即坡角的正切值。那么倾斜角的正切值又表示什么呢?

课堂活动
判断对错
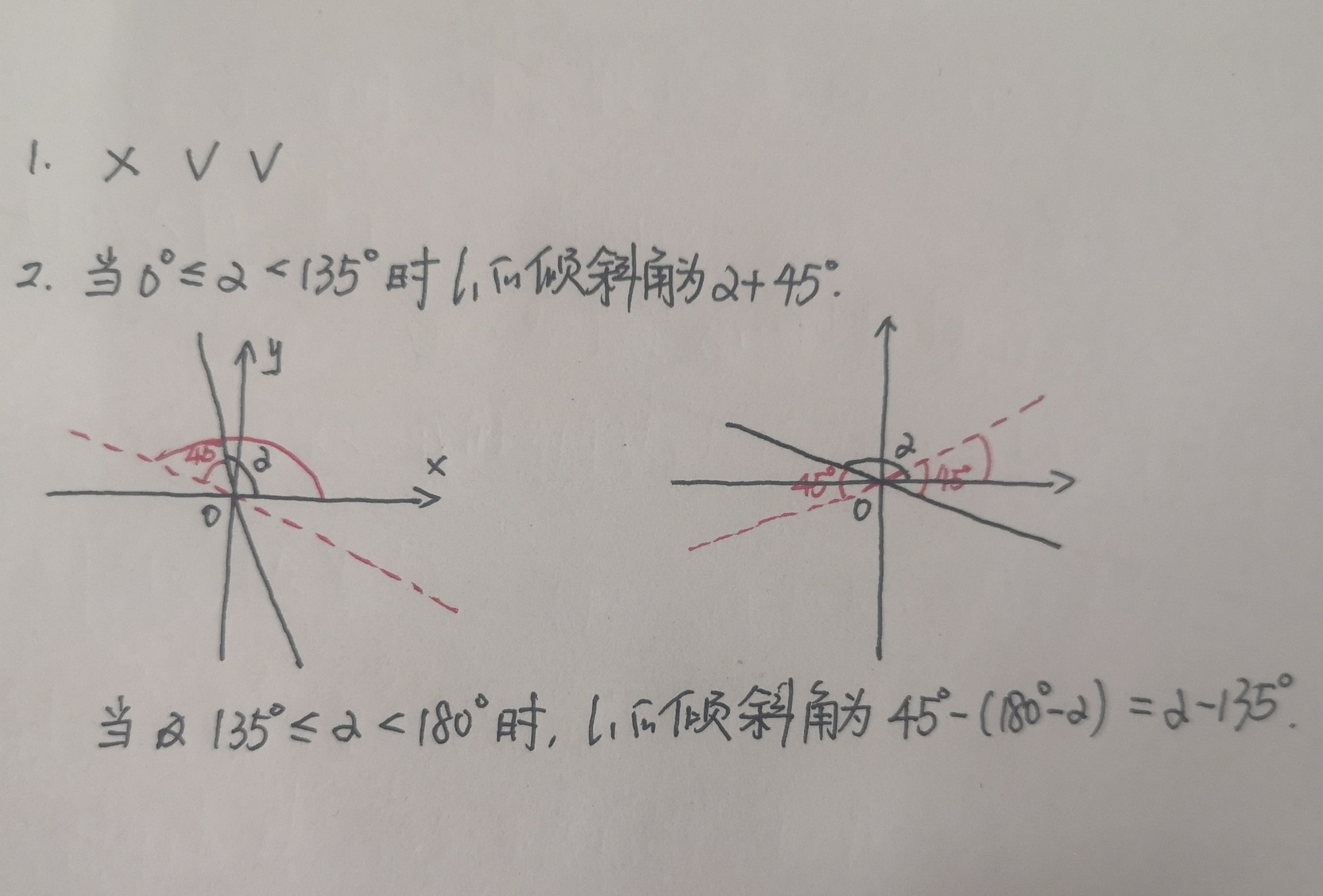
1、倾斜角是90度的直线,斜率不存在;
2、倾斜角的范围大于0度小于180 度;
3、直线都有倾斜角,但不一定都有斜率;
4、直线的倾斜角越大,斜率越大;
5、平行于x轴直线倾斜角是0或180 度;
6、垂直于x轴的直线倾斜角为90度,斜率不存在。
设计意图:通过希沃白板的动画演示、画板演示、课堂活动等技术手段讲授斜率的概念。通过坡度比知识的迁移,引出斜率的概念,对斜率的概念辨析主要是通过动画演示,与正切函数在0o-180o之间图像的分析,得出倾斜角与斜率的关系,让学生更加了解倾斜角和斜率。
播放倾斜角和斜率的视频。
本节课,我们在平面直角坐标系中,讨论了确定直线位置的几何要素,即两点确定一条直线以及一点和一个方向确定一条直线。并从形和数的角度利用倾斜角和斜率来刻画直线的倾斜程度,即表示了直线的方向,并探讨了倾斜角、斜率与直线上两点坐标的关系。在此过程中体会到了数形结合数学思想以及将几何问题转化为代数问题的化归转化思想。
设为正确答案