- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《扇形》这部分内容来源于人教版数学六年级上册75页,是五单元《圆》这个单元知识的拓展与延伸。苏教版五年级下册九单元也有这一内容。
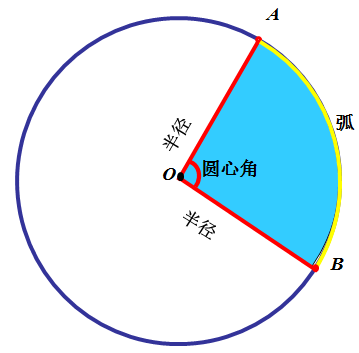
教材从“扇贝”“扇形藻”“折扇”这几个带“扇”字的物体引入,让学生初步建立扇形的印象。接着,教材通过一个图片让学生充分感知“弧”“扇形”“圆心角”的概念。然后,教材强调了“在同一个圆中,扇形大小与这个圆心角的大小有关”这一概念。最后,教材通过小精灵的提问让学生感受“以半圆为弧的扇形的圆心角度数就是180度”“以四分之一圆为弧的扇形圆心角度数就是90度”的道理。内容简单、丰富、有层次。
通过仔细研读教材75页发现,教材新授难度并不大,对学生的要求也不高,但是练习十六的一道习题深深吸引了我们团队,求扇环的面积。其实新授部分并没有要求同学们求扇形的面积,怎么会有扇环的面积呢?这就让我们深刻思考“教是为了不教”这句话,我们教给孩子的知识是有限的,但是学生的学习力是在无限生长,如何培养学生的“学习力”是我们一直需要思考的事。学生的学习力被激发,扇形的面积会自然而言被探究出来,扇环面积也就是水到渠成的事。当然,我们要对学生有分层的要求,不是所有孩子都能突破这一难点,保护学生的学习兴趣和探索的欲望是非常重要的。
《扇形》这个内容是人教版六年级上册第五单元的内容,学生学习了《圆的认识》,知道“圆心”“半径”“直径”等基本概念,也学习了圆的周长、圆的面积这一系列知识,更学习了“圆中方”“方中圆”这一拓展知识。可以说学生对圆的体验是很丰富的。在这样的基础上学习《扇形》,毫无疑问,是要让学生能够将扇形和圆充分进行联系。
其实,很多学生学圆到最后都被周长和面积公式打上了深深的烙印,对于探索过程的记忆就慢慢弱化了,但是探索的能力还是逐渐被激发出来了,正是因为这样,我对学生学习扇形,去探索扇形当中更加复杂的问题拥有非常强烈的信心。
六年级的孩子创造力和探索能力是非常强大,老师也要放心大胆地交给他们任务,他们往往能带给我们超乎想象的惊喜。
知识与技能:理解和建立扇形概念,认识圆心角和弧,充分感受扇形大小及所占相应圆的比例。
过程与方法:在认识圆心角和弧的过程中,培养学生的观察能力、想象力以及自学能力。
情感态度与价值观:学会欣赏数学的美,热爱生活。
教学重点:建立扇形概念。
教学难点:理解圆心角的大小与扇形大小的关系,充分感受扇形所占相应圆的比例。
扇形
(一)激趣导入
师播放音乐,6个同学进行中国传统扇子展示。(绸布扇、网红扇、古典扇、团扇)
师:这几位同学手里拿的是什么?
生:扇子
师:中国文化源远流长,不管是在舞台表演还是在现实生活中,扇子都扮演了非常重要的角色,请你们按照形状将这些扇子分为两类。(1生操作)
师:你是怎么分的?
生:我将折扇分为一类,其它的分为第二类。
师:你真善于观察!同学们,折扇是扇子最经典的形象,在数学中,我们也要学习以折扇为原型的形状——扇形。(板书课题:扇形)
(二)探索新知
1.自主学习,感知概念
师:要想真正理解什么是扇形,我们必须先去明确三个概念:弧,圆心角,扇形。你同学们打开数学书75页,一分钟自学时间。
师观看学生自学并提问:我想采访一下你,你认为自学的时候有什么需要提醒同学们的吗?
生:将重要的地方标记出来。
师:做笔记是非常好的学习习惯。
师:时间到!有信心接受我的考验吗?请关上书。
(1)这些是弧吗?为什么?
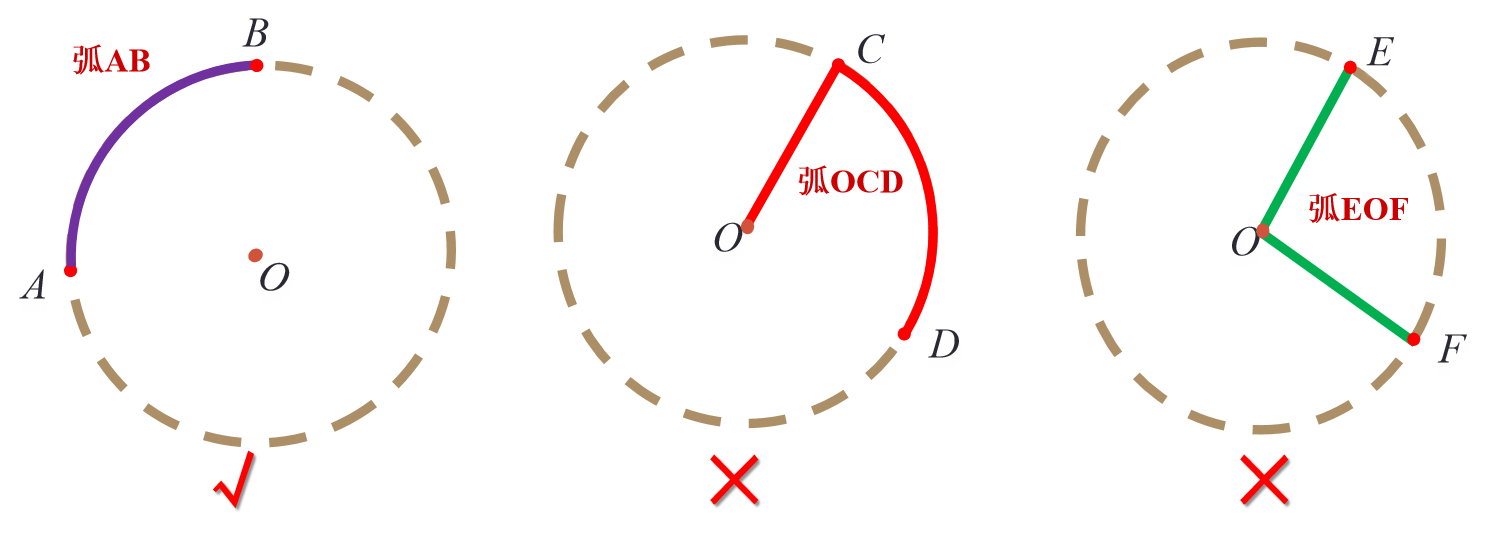
生:第一个是,第二、第三个不是。
师:为什么?
师生一起得出:圆上A、B两点之间的部分叫做弧,读作“弧AB”。关键词是“圆上”。(板书再次演示弧)
师:这样的弧还有多少条?
生:无数条
(2)哪些是圆心角?为什么?
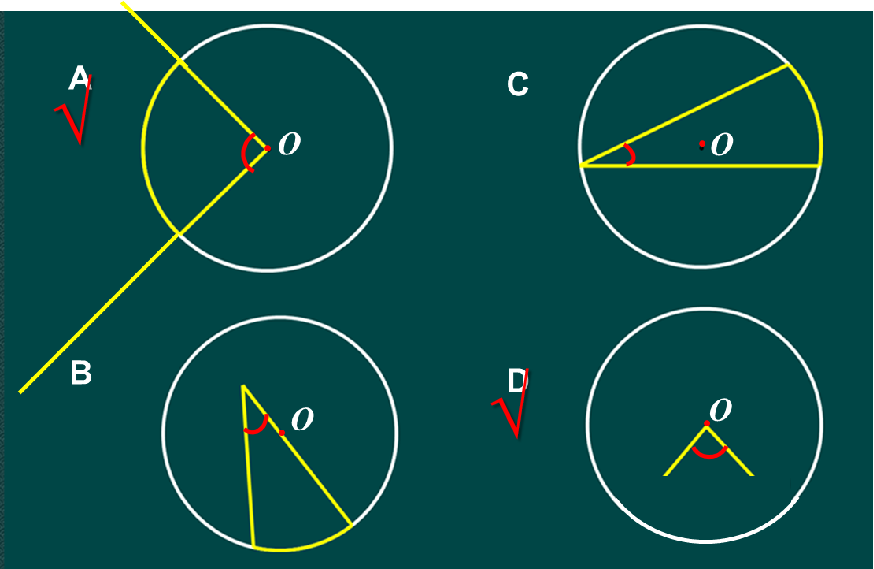
生:第一个和第四个,因为它们过了圆心
师:所以,什么样的角叫做圆心角?
师生一起得出:像图A、D这样顶点在圆心的角叫做圆心角。关键部分是:顶点在圆心。(补充提问:跟两条边的长度有关系吗?)
(3)哪些是扇形,为什么?
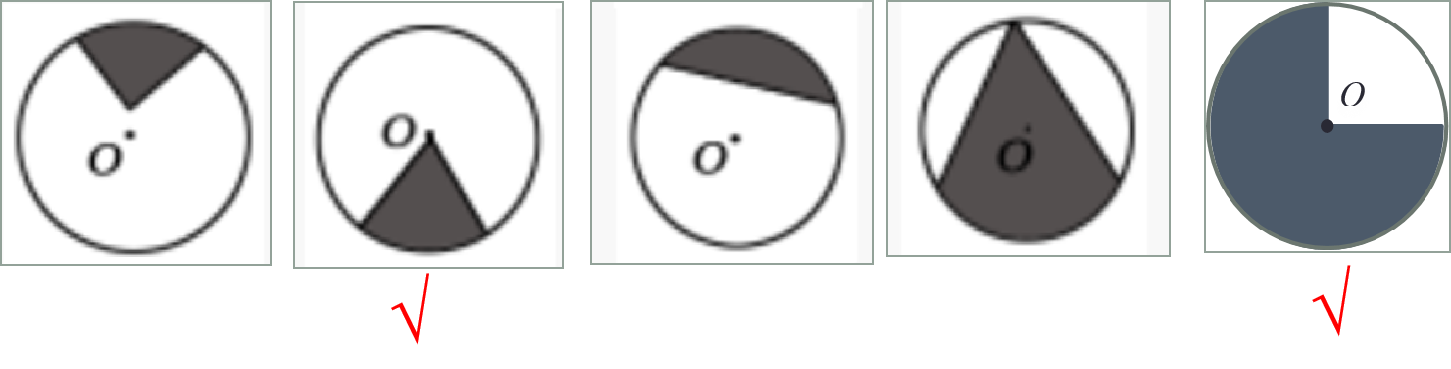
生:第二个和第五个,因为第二个和第五个是由弧和半径围成的,其它几个都没有经过半径。
师:那是黑色部分是扇形还是白色部分是扇形呢?
生:黑色部分和白色部分都是扇形。
师:为什么?
师生一起:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。(师在黑板上边画边讲解)
师:这里面哪些词比较关键?
生:一条弧、两条半径、围
师:找关键词是一个非常好的学习方法!其实我们扇子中固定扇子这枚螺丝就类似于圆心,这些木条就类似于半径,扇叶上面这一条边就类似于弧。(拿一把扇子演示)
2.聚焦核心,深入剖析
师:扇子有大有小,扇形肯定也是有大有小的(拿两把扇子继续演示)。请你们猜想:扇形的大小和什么有关?
生汇报:与圆心角和半径都有关。(师先用一把扇子开合的过程来演示,再用两把扇子对比演示)
师引导学生总结:同一个圆中,扇形的大小与这个扇形的圆心角的大小有关,圆心角越大,扇形越大。圆心角相等时,半径短的扇形面积小,半径长的扇形面积大。(PPT展示)
3.动手实践,升华认知
师:你们的学习能力很强,我相信你们的动手能力也很强!
任务1:请折一个圆心角为180度的扇形。
师采访:你是怎么折的?
生:圆心角为180度的扇形就是半圆,对折就好了。
师:你们也是这样折的吗?请你们猜想一下:这个扇形的面积和圆的面积有什么关系?
生:这个扇形面积就是圆面积的一半。
师:越来越有意思了,我们继续来看。
任务2:请折一个圆心角为90度的扇形。
师采访:你是怎么折的?
生:先对折,再对折就可以了。
师:请举起你们的作品给我看看!现在又请你们猜想一下:这个扇形的面积和圆的面积有什么关系?
生:这个扇形面积就是圆面积的四分之一。
师:你们太厉害了,现在请你们大胆猜想:任意一个扇形的面积和它所处这个圆的面积有什么关系?
生思考得出:和圆心角所占比例有关。
师:学霸在这里,请鼓鼓掌,数学家就是通过这种方法推导出扇形面积的计算公式的,这也是我们初中要学习的内容,你真了不起。
师:能和你们一起学习,真开心,接下来我们一起去开运动会吧!我需要两名运动员。
(三)练习巩固(希沃课堂活动)
森林运动会(判断题)
(1)顶点在圆内的角叫圆心角。 ( × )
(2)扇形的大小只与半径有关。 ( × )
(3)圆心角为60度的扇形,它的面积占整个圆的三分之一。 ( × )
(4)半圆也是一个扇形。 ( √ )
(5)一个圆内剪一个扇形,剩下的部分还是扇形。 ( √ )
(四)总结提升
师小结:同学们,数学源于生活又高于生活,只要你善于观察,勤于思考,你就是一个小小数学家!
设为正确答案