- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



初中阶段,主要以“两点之间,线段最短”,“连接直线外一点与直线上各点的所有线段中,垂线段最短”,为理论基础,有时还要借助轴对称,平移,旋转等变换进行研究。
本节内容是在学生学习平移、轴对称等变换的基础上对数学史中的一个经典问题 ------“将军饮马问题”为载体进行设计,开展对“最短路径”的课题研究。
本节课内容选自湘教版《数学》八年级上册第94-95页.
这一阶段,学生理解能力和抽象思维水平不高,处于直觉经验型思维向逻辑思维的过渡阶段,辩证思维还只是处在萌芽和初始的状态上.最短路径问题从本质上说是最值问题,作为初中生,在此前很少涉及最值问题,解决这方面问题的数学经验尚显不足,特别是面对具有实际背景的最值问题,更会感到陌生,无从下手.在学生已有知识“两点之间,线段是最短”,“三角形中任意两边之和大于第三边”的基础上,如何利用轴对称的方法将两条同侧的线段之和转化为两条异侧线段和的最小值有一定的困难,本节课主要需要引导学生利用线段垂直平分线的性质将两条同侧的线段之和转化为两条异侧线段和,并探究其最小值.
知识技能:
能利用轴对称变换解决简单的最短路径问题,体会图形的变换在解决最值问题中的作用,感悟转化思想.
数学思考:
通过例题和变式的解答,加强对“将军饮马”模型的理解和运用,发展学生灵活运用数学知识、解决问题的能力,培养直观想象、数学抽象、逻辑推理的数学素养.
问题解决:
能利用轴对称变换解决日常生活中的实际问题,学会化“折”为“直”解决问题,培养学生的分析、解决问题的能力.
情感态度:
通过学生动手操作和合作探究,培养学生的团队意识与勇于探究的精神;通过对猜想的合理探索和严格证明,增强学生的应用意识和语言表达能力,培养学生对数学的兴趣和钻研精神.
重点:利用轴对称变换将最短路径问题转化为“两点之间,线段最短”问题.
难点:如何利用轴对称的方法将两条同侧的线段之和最小转化为两条异侧线段和最小“,而不是”将最短路径问题转化为线段和最小问题.


唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河。 ”诗中隐藏着一个有趣的数学问题。如图所示:诗中的将军在观望烽火之后从山脚的A地出发到河边l饮马,然后再回到B地宿营怎样走才能使得总路程最短呢?

抽象:如图,在直线l上找一点P,使得PA+PB最小?
活动一:自主探究,得出方案.
学生在动手画一画,找出所有可能的点,并和组员交流,教师展示学生所作成果并比较。
希沃同屏展示学生答案。
思考:为什么这样作图?
活动二:几何画板,比较方案.
利用几何画板展示每种方案所得到的AP+BP的值,比较哪个值最小,得出猜想.
活动三:利用轴对称变换,证明猜想.
学生小组合作探究,证明结论.
教师总结:
证明:在直线l 上任取一点Q,(与点P不重合)
连接AQ,BQ,A′Q
由轴对称的性质可知:
AP +BP= A′P +BP= A′B,
AQ +BQ= A′Q+BQ.
由两点之间线段最短可知:A′B <A′Q+BQ
∴ AP + BP < AQ +BQ,
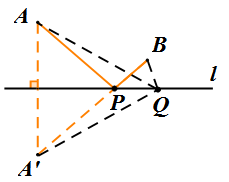

将军从图中的A地出发,到一条笔直的河边饮马,然后到B军营休息.他到河边何处饮马时所走的路线最短?
例 如图,在等边△ABC中,AD⊥BC,E为AC的中点,请在线段AD上找一点M,使得ME+MC的值最小.
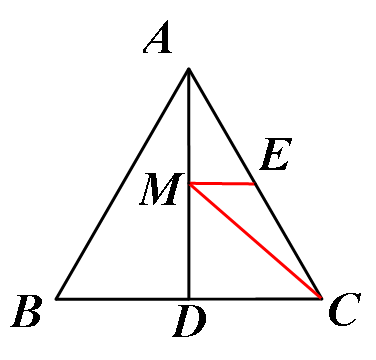
变式训练:
若AD=6, 求△CME周长的最小值.
设为正确答案