- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间




恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



1.线段的垂直平分线的性质在以后的学习中经常要用到的,它是在认识了轴对称的基础上进行的,
是今后证明线段相等和直线互相垂直的依据,因此本节课具有承上启下的重要作用。
2.前面已学过线段的垂直平分线的概念,本课是进一步理解线段垂直平分线的性质,
在计算、证明、作图中有着广泛的应用,应注重提高综合运用知识的能力。
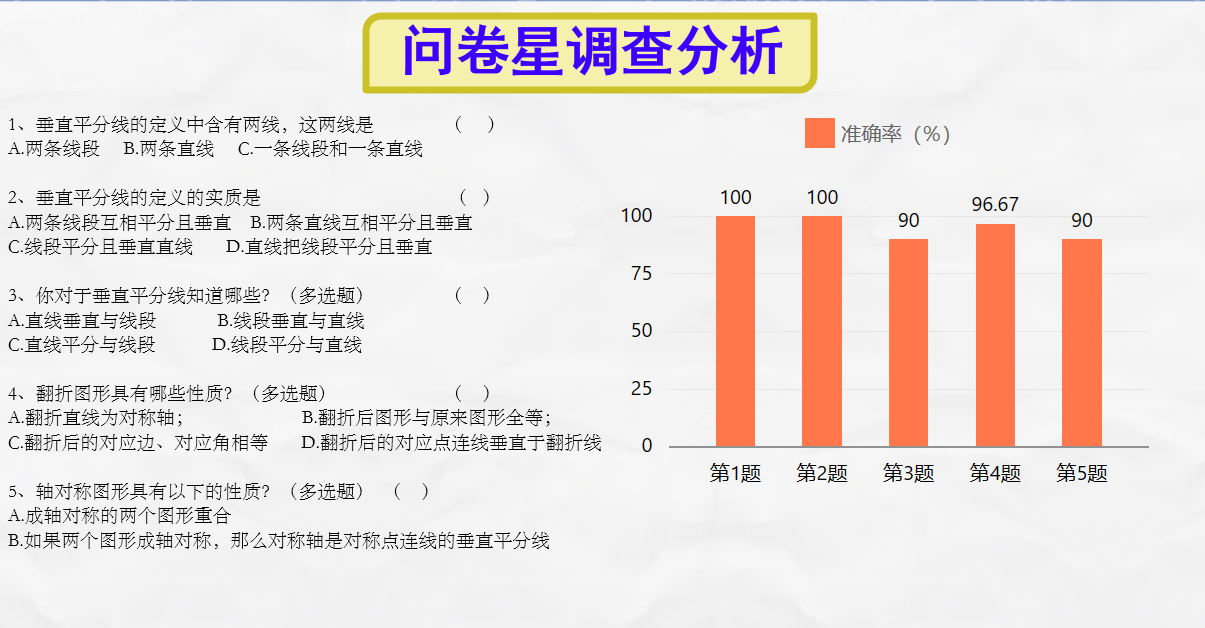
通过七年级的几何知识学习,学生已经具备一定的独立思考和探究能力,并能在探究过程中形成自己的观点。事实上,通过对课前的问卷星调查结果分析,我们发现学生确实已经很好地掌握了垂直平分线的定义以及轴对称相关知识;这为线段垂直平分线的性质的探究、学习以及应用提供了知识准备。
1.通过实践操作,引导学自主探索垂直平分线的性质,进一步发展学生的推理证明意识和能力;
2.提高学生知识的迁移与应用能力,使得大部分学生能运用线段的垂直平分线性质解决相关题型;
3.通过信息技术的融合,多种教法并用,激发学生学习数学的兴趣与积极性;
重点:线段的垂直平分线性质的猜想与证明
难点:线段的垂直平分线性质用于求数学问题中线段、周长的长度以及生活问题的应用
线段垂直平分线的性质定理
线段垂直平分线上的点到这条线段两端的距离相等
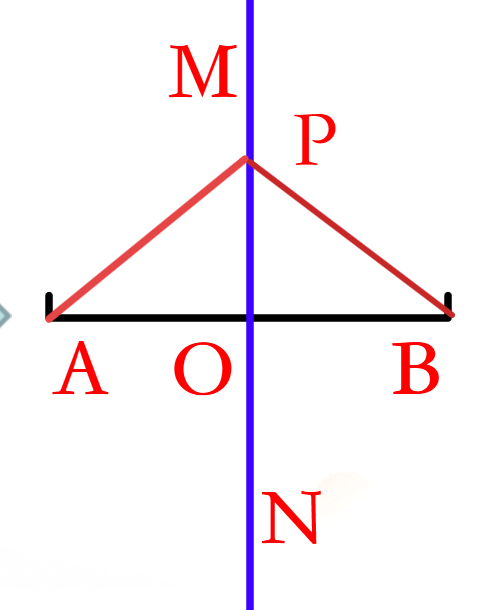
几何语言:
∵点P在线段AB的垂直平分线上
∴PA=PB
教师用多媒体演示:
1,根据风筝模型引入垂直平分线的定义,加以复习
(提问学生,并让学生回答)
2,提问PA是否与PB相等,引出本节课垂直平分线性质的探讨
(提问学生,激发学生对于垂直平分线性质的求知欲,为动手操作做铺垫)
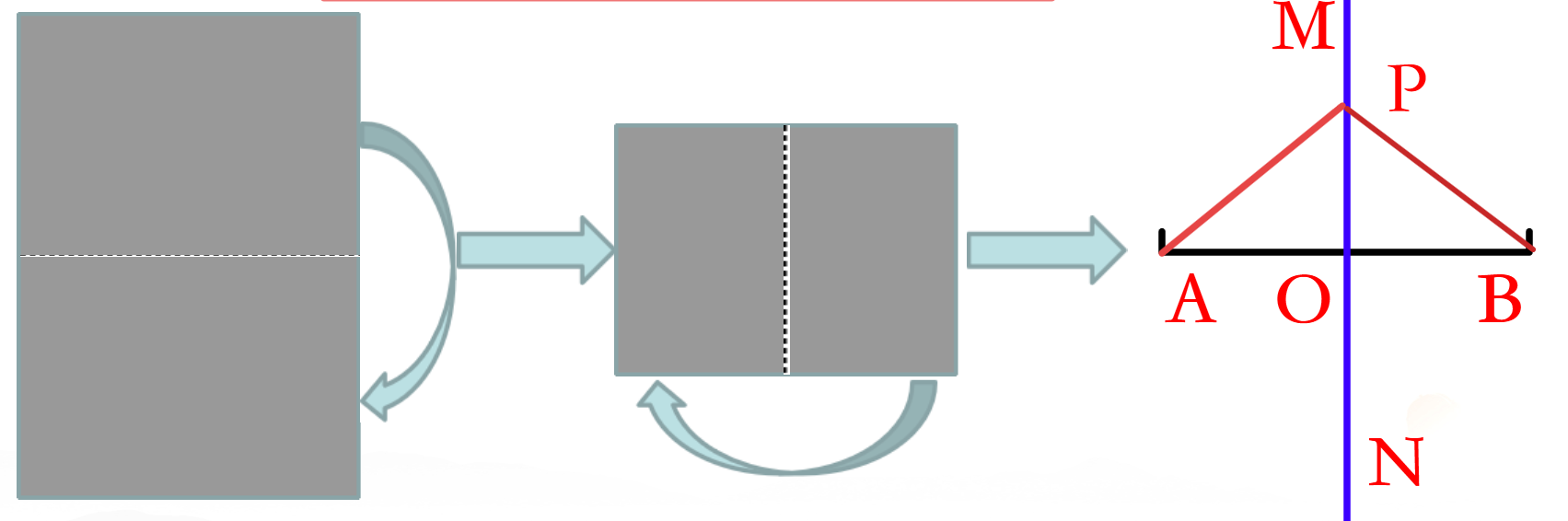
1,老师带领学生按示意图折纸操作
2,让学生独立测量PA与PB的长度
3,让学生对比测量结果,提问有什么发现?
4,运用同屏技术展示任意四位学生的折纸结果
(由个人选取的点的特殊性到全班同学选取点的普遍性)
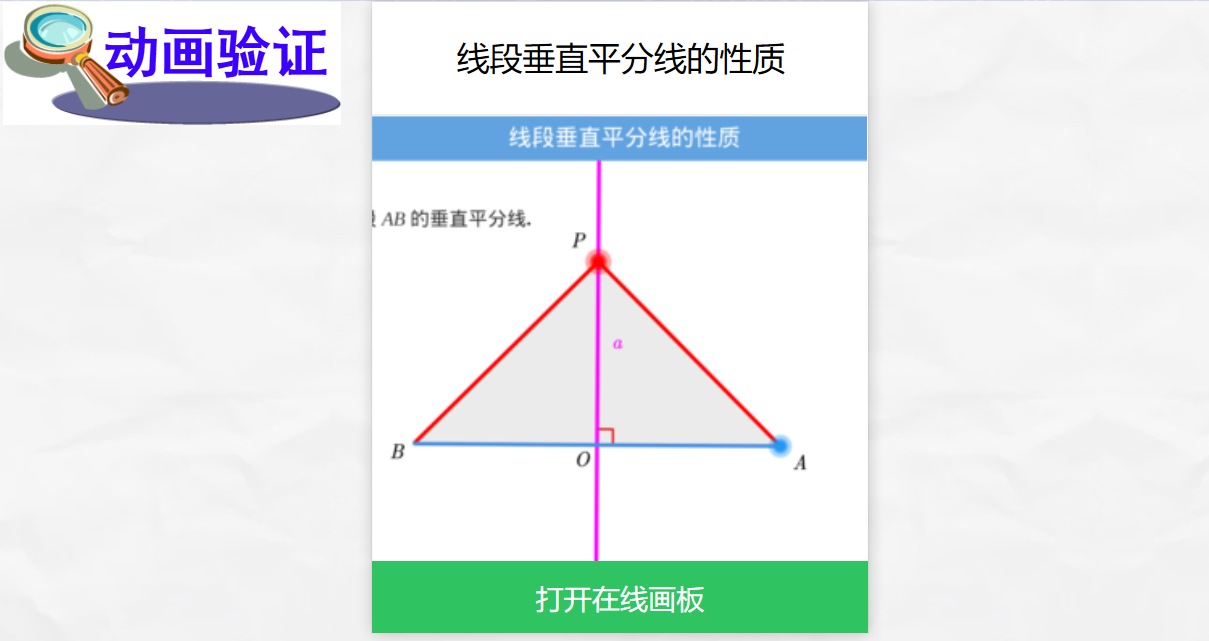
利用希沃课件中的数学画板,打开线段垂直平分线的性质的在线画板
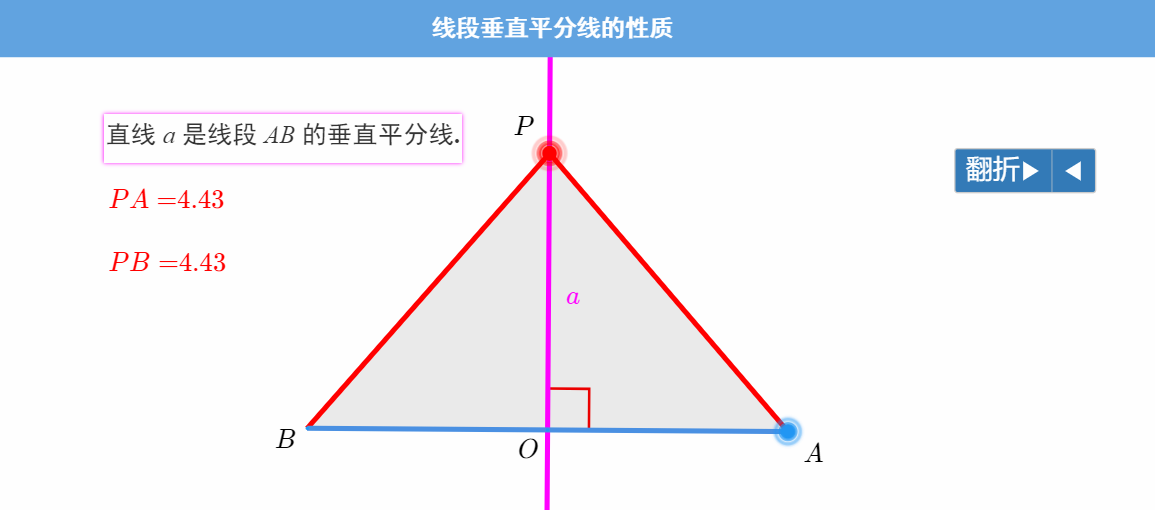
学生观察结果:1.无论P点位置如何移动,从数值上看PA=PB
2.无论P点位置如何移动,从折叠上看都有PA与PB重合
(教师点明这个几何动画是利用轴对称的知识验证)
引导学生小组讨论归纳:线段垂直平分线上的点到这条线段两端的距离相等
(教师运用计时器,提高讨论效率以及课堂的掌控度)

解:∵ MN是线段BC的垂直平分线,BM=7
∴ CM=BM=7
又∵ CΔBMC =23
∴BM+MC+CB=23
∴BC=23-CM-BM=23-7-7=9
注意:1,老师运用计时器,提高学生的讨论效率以及课堂的掌控度
2,老师要引导学生理清证明的思路和方法并板书完整的证明过程

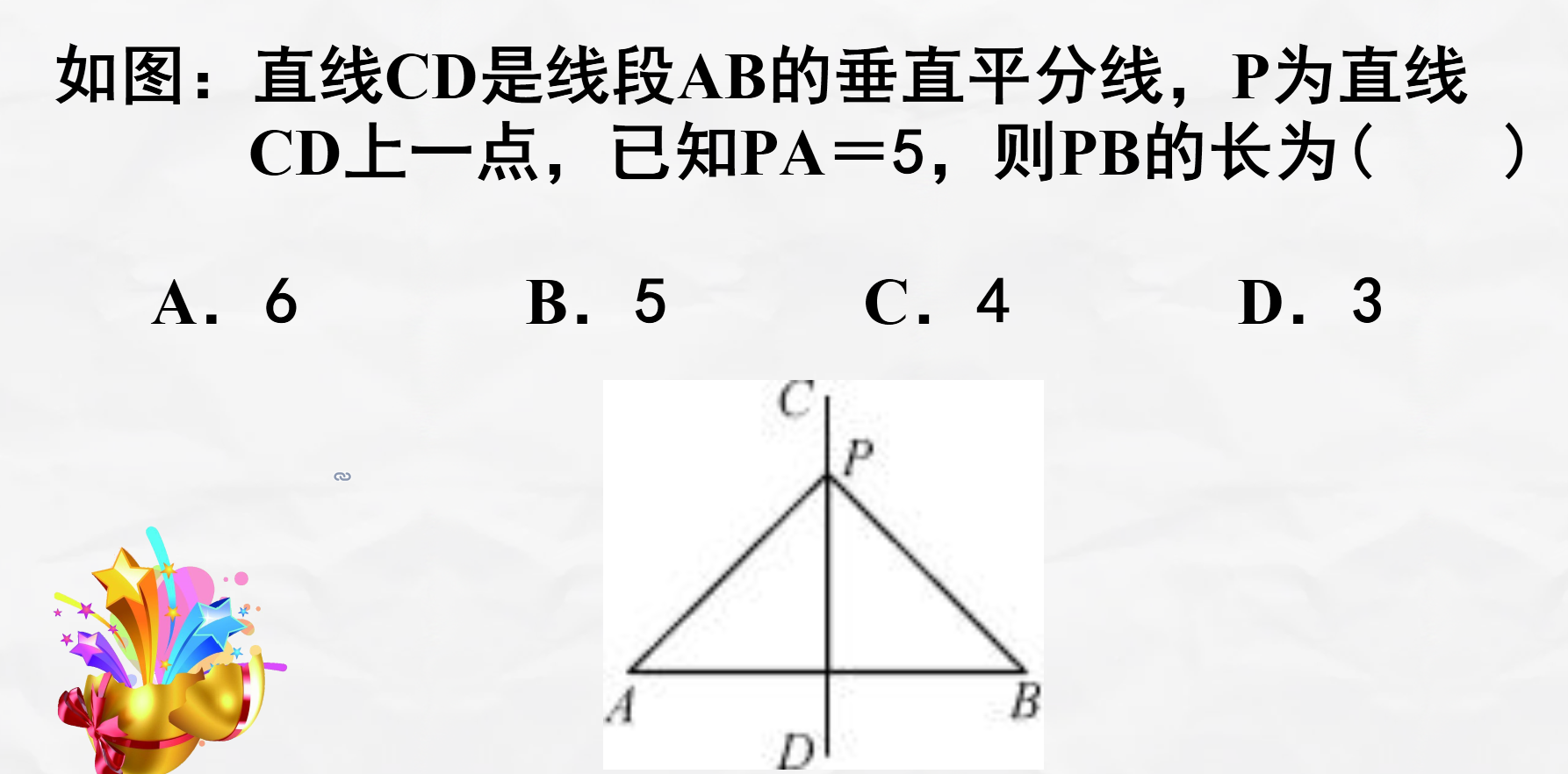

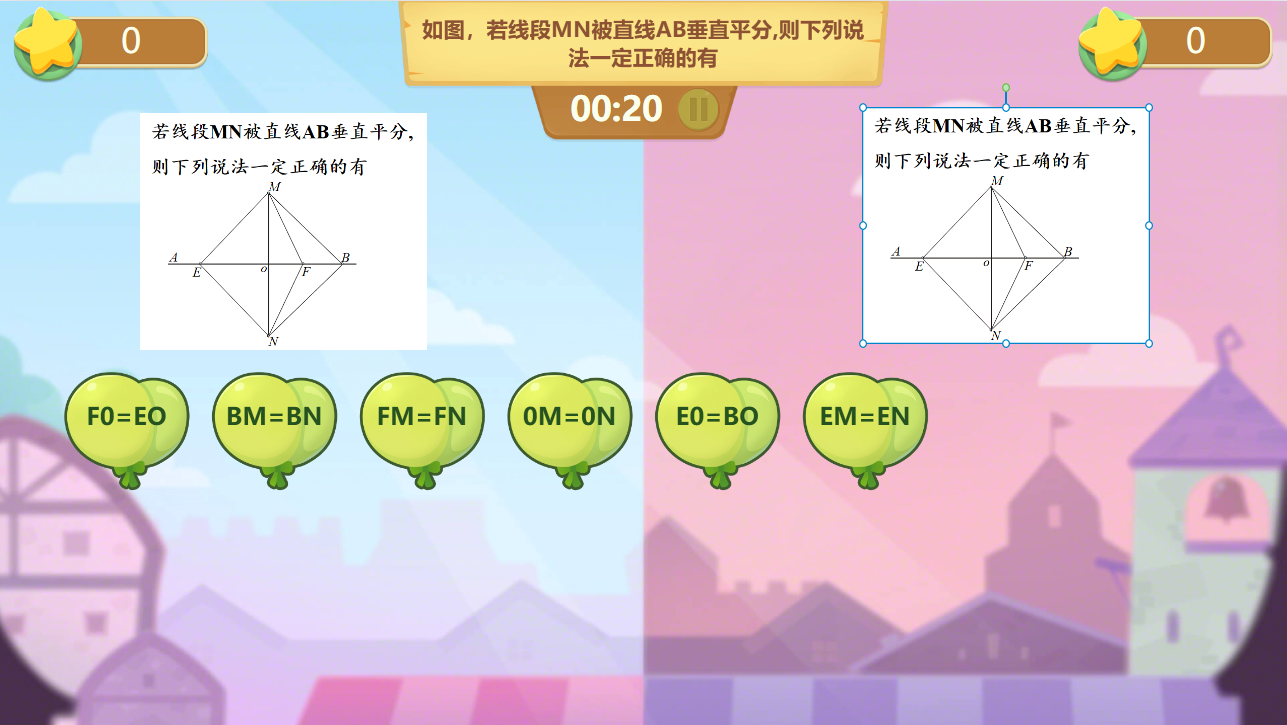
说明:1,运用超链接技术、希沃课堂活动,制作课堂砸金蛋、知识竞赛等游戏,
提高学生的兴趣,巩固性质定理的内容并加以应用
2,教师运用点名器,随机抽取学生来进行砸金蛋、知识竞赛活动
设为正确答案