- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
从实际生活入手介绍圆锥曲线，从绘制圆的方法中绘制椭圆
能通过绘制椭圆的过程，认识椭圆的几何特征，给出椭圆的定义，能通过建立适当的坐标系，根据椭圆上的点、满足的几何条件，列出椭圆上的点的坐标满足的方程，化简所列出的方程得到椭圆的标准方程，能在直观认识椭圆的图形特点的基础上.
能通过关于椭圆的实际问题转化为关于椭圆的数学问题，运用椭圆的定义、标准方程及简单的几何性质解决关于椭圆的数学问题。学生对坐标法有初步的认识，通过直线和圆的方程学习，对坐标法研究曲线的基本思想和与方法有了了解，但不善于自觉运用坐标法。在学习中可能会遇到如何抽象出椭圆的几何特征以及如何建立适当的坐标系等这些问题。
本单元的内容是在学生学习直线和圆的方程的基础上，先抽象椭圆的几何特征，然后建立它的标准方程，再利用方程研究它的几何性质，并利用它们解决简单的实际问题。从知识的前后联系看，本单元是坐标法的进一步运用，所要解决的仍然是解析几何的两个基本问题，建立曲线方程，通过方程研究曲线的几何性质。
教学目标：
1. 能通过观察平面截圆锥认识到：当平面与圆锥的轴所成的角不同时，可以分别得到圆、椭圆、双曲线和抛物线．能通过实例知道圆锥曲线在生产、生活中有广泛的应用．能通过章引言初步认识本章的学习内容、学习方法与学习价值．
2.认识形成能通过实际绘制椭圆的过程认识椭圆上点的几何特征，给出椭圆的定义,发展数学抽象素养．
3.能通过实际图片信息，从天上到日常生活，让学生意识到数学知识就在我们身边，神舟十二号、广州塔、鸟巢的介绍，培养学生的爱国热情，增强民族自豪感
1 理解圆锥曲线 、掌握椭圆的定义、焦点 、焦距的定义
2 从实际问题中抽象成数学问题
椭圆的定义
一 圆锥曲线 ：椭圆 抛物线 双曲线
二 椭圆定义：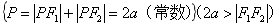
焦点：两个定点
焦距：焦点的距离
注：若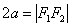
则轨迹为线段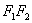
引导语：
数学是宇宙事物关系的抽象，是研究宇宙的数与数、形与形、数与形间的关系的一门学科！前面我们用坐标法研究了直线圆及其位置关系，生活中还有一些有用有趣我们还不太了解的曲线有待于我们去探究!
6月17号神舟十二载人飞船发射完满成功，9月17日安全返回地球，接着神舟十三号又即将发射，这是我们每个人值得骄傲的事情，同学们，这些天体运行的轨道是？椭圆；广州塔的外形线是？双曲线，鸟巢是由什么曲线做成的？抛物线，
还有日常生活大大小小的物件用到了曲线，这些曲线就是我们今天要学圆锥曲线！那么什么是圆锥曲线呢？
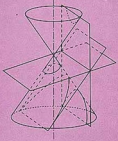
问题1：如图1，用一个垂直于圆锥的轴的平面截圆锥，截口曲线（截面与圆锥侧面的交线）是一个圆. 如果改变截面与圆锥的轴所成的角，会得到怎样的截口曲线呢？
师生活动：教师通过信息技术演示，引导学生认识截面与圆锥的轴所成的角不同时得到的不同的截口曲线，并指出它们分别是椭圆、双曲线、抛物线（图1），通过截面的动态图感受数学美！
设计意图：实际生活中的图片都是我国有代表性的事物，让人联想神舟飞船、奥运会、广州亚运会等重大事件，有利于增强学生的民族自豪感，激发学生的学习热情！问题1重在引发学生思考，并不要求学生解决．这个环节的教学目的是明确本章内容的意义与价值，促进学生形成积极探究的心理倾向．
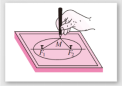
问题2：在平面内到定点距离等于定长的点的集合为圆，我们取一条定长的细绳，把它的两端都固定在图板的同一点，套上铅笔，拉紧绳子，移动笔尖，这时笔尖（动点）画出的轨迹是一个圆．如果把细绳的两端拉开一段距离，分别固定在图板的两点F1，F2（图2），套上铅笔，拉紧绳子，移动笔尖，画出的轨迹是什么曲线？
追问1：在这一过程中，移动的笔尖（动点）满足的几何条件是什么？
追问2：当动点到两定点间距离和与两定点间距离的大小关系发生变化时动点的轨迹会发生什么变化？
请同学们拿出事先准备好的铅笔细绳，图钉和图板尝试一下
（学生动手，两两合作，2分钟）
小组上台展示，老师强调每个小组的绳长基本相同
老师问：同学们看每个小组展示椭圆有什么变化？（讨论1秒）
老师问：你们发现了什么现象？
师生活动：教师利用动态图模拟演示椭圆绘制过程，呈现所画的曲线具有共同的特点，然后用数学语言刻画这些曲线上点的几何特征．
设计意图：由实际操作，强化学生对椭圆的几何特征的认识. 在探讨定点间距离与动点到两定点间距离和的大小关系发生变化（量变）时动点的轨迹相应发生的变化（质变）的过程中再一次渗透辩证唯物主义思想。
问题3：你能用精确的数学语言刻画椭圆吗？
追问：椭圆定义中我们应该特别关注那些要素?
师生活动：尝试用精确的数学语言给出椭圆的定义．在此基础上，教师关注学生对定义中相关用语及符号表示：“平面内”“定点”“距离之和”“常数”“常数大于两定点间的距离”“点的轨迹”的使用是否准确． 老师在黑板上用集合语言板书椭圆的定义
老师板书：
椭圆定义：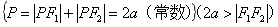
焦点：两个定点
焦距：定点距离的
注：若F1F2=2a 轨迹为线段F1F2
设计意图：通过强化椭圆的概念的抽象与建立过程，增强学生思维的严谨性与语言表达能力．
现实背景-----曲线的概念----------曲线方程（接下来）
设为正确答案
湘教智慧云 
贝壳网公众号