- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课的部分内容在小学已经有初步认识,尽管具有一些几何知识,但他们对几何的认知能力仍处于低级阶段,空间观念、想象力还有待进一步提高;在本课中,要加强学生对基本几何与其展开图的关系,一个立体图形以不同方式展开可得不同的表面展开图的学习;同时也应该让学生明白并不是所有的立体图形都有表面展开图。
教学模具:圆柱、圆锥、三棱锥、四棱锥、五棱锥、三棱柱、长方体、正方体、12个全等的等边三角形
1、认识立体图形与平面图形的关系。一个立体图形按不同方式展开可得不同的表面展开图。
2、通过观察和动手操作,经历和体验图形的变化过程,培养实验操作的能力,发展空间观念。
3、主动探究,敢于实践,勇于发现,合作交流。
重点:基本几何体与其展开图的关系,一个立体图形以不同方式展开可得不同的表面展开图。
难点:正确判断哪些平面图形可折叠为立体图形。
在教师问题的引导下,先让学生自主探索、教师巡回点拨,后班级交流,通过生生、师生互动生成
一、创设情境,引入课题:
设计意图:通过问题引发学生的思考和探究的欲望,引起学生的学习兴趣,进一步培养学生的空间想象能力。
小壁虎遇难题:
有一天壁虎在圆桶的下方,发现上方有一只蚊子,饥饿的它要想尽快吃到蚊子,应该走哪条路最近呢?
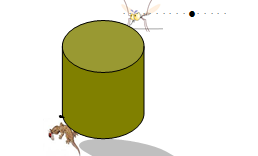

学生活动:学生观察、体会。
二、观察操作,认识感受:
在我们的实际生活中常常需要对物体进行包装,例如在对电视机进行包装的时候,就需要根据电视机的表面展开图来裁剪纸张。为此我们本节课要讨论的是一些简单多面体的表面展开图。(出示课题:立体图形的表面展开图)
设计意图:先想象再动手验证,通过实践加深对图形表面展开图的认识。
1.感知立体图形的表面展开图
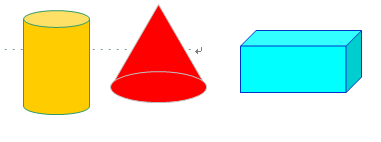
2.动手操作,经历立体图形的表面展开图
“做一做”:12个一样大的等边三角形,粘贴成如下图所示的三种形状,你能想像哪一个可以折叠成多面体?动手做做看。

图(1) 图(2) 图(3)
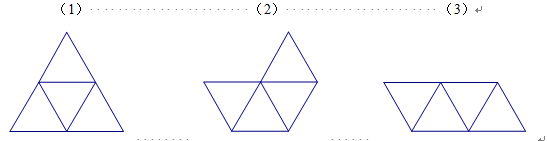
从学生动手的结果,我们易知,图(1)、图(3)可以折叠为多面体,图(2)不能折叠成多面体。
问:通过动手实践,你能感受或认识平面图形和立体图形的关系吗?
沿着多面体的一些棱将它剪开,可以把多面体展开成一个平面图形,我们把它叫做这种多面体的表面展开图。
上面的图(1)、图(3)实际上是由三棱锥展开而成的平面图形,我们把它叫做三棱锥的表面展开图。
学生活动:学生动手,用提前准备好的图形进行试折。
设计意图:以合作交流的形式,加强学生的合作意识。
3“想一想”,拆一拆
下图是哪些多面体的展开图,你能说出这些多面体的名称吗?
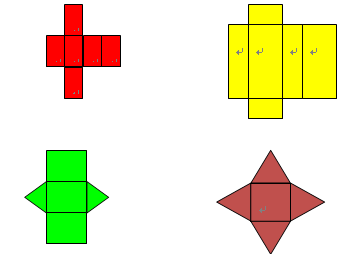
4 . 知识应用,培养学生空间观念
下列图形是某些多面体的表面展开图,你能说出这些多面体的名称吗?
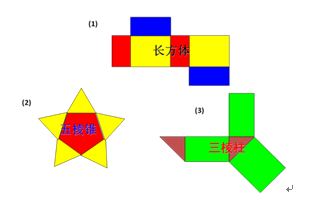
学生活动:学生观察、思考,分组讨论后回答。
设计意图:通过对正方体这一常见图形的探究,加深对这种图形的巩固,并在探究中感受学习的乐趣。
5.质疑
设计意图:通过对正方体这一常见图形的探究,加深对这种图形的巩固,并在探究中感受学习的乐趣。
同一个立体图形,按不同的方式展开得到的表面展开图是否一样?
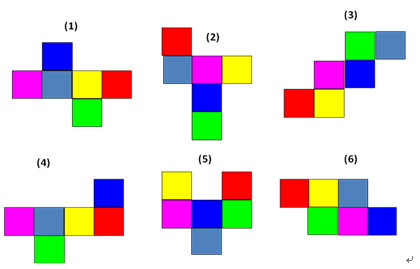
说明:同一个立体图形,按不同的方式展开得到的表面展开图是不一样的.
6. 归纳:
将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种:
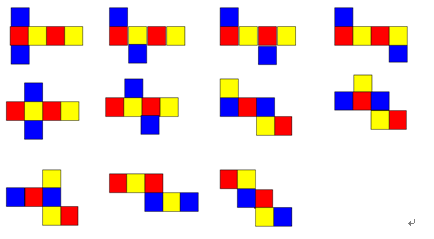
学生活动;学生思考后回答,集体评议。
设计意图:通过“考考你”的活动,加强对学生的空间想象能力的培养,以“体、面、点”的形式进行强化。
7. “考考你”活动
1如果“你”在前面,那么谁在后面?
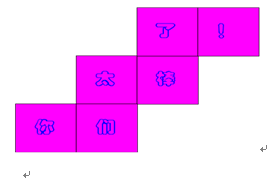
学生活动:学生先独立完成练习,然后合作小组进行交流评议,最后由组内选出代表集中交流评议。
三、知识小结:
设计意图:发挥学生的主体意识,培养学生的归纳能力。
1、立体图形是由平面图形组成的。
2、能根据展开图判断立体图形。
3、能判断平面图形是否为立体图的展开图。
4、并不是所有的立体图形都有平面展开图。如:球体
学生活动:学生总结,教师作概括。
四、作业设计
(1)教材第131--132页练习第1、2、3题。
(2)制作精美的盒子送给父母、老师或朋友。
【教学目标】
1、使学生进一步认识立体图形与平面图形的关系,了解多面体可由平面图形围成。
2、通过观察和动手操作等活动,加强对立体图形与平面图形的认识和感受,经历和体验图形的变化过程和变换思想,进一步形成和发展学生的空间观念和几何直觉。
3、结合培养学生的空间想象能力和以发散思想为核心的创新思维能力。
【教学重点、难点】
重点:进一步认识立体图形与平面图形的关系,经历和体验图形的变化过程。
难点:如何将平面图形想象还原成立体图形
【教学准备】
多媒体课件,适当放大本节课中的所有平面图形发给学生,用纸带粘成的正三棱锥模型,剪刀,透明胶,纸带等。
【教学过程】
一、创设问题情境:
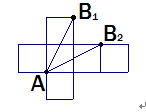
1、 如图,一只蚂蚁在正方体箱子的一个顶点A,它发现相距它最远的另一个顶点B处有它感兴趣的食物,这只蚂蚁想尽快得到食物,哪条路径最短?试在图中将路线画出来。
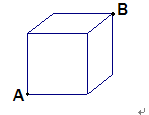
2、 怎样用平面图形围成立体图形?
(1) 同学们看我手里拿着这张长方形的纸,把它卷起来(把长方形的短边卷一下,并使两条长边靠拢),大家看得到的是什么立体图形?还可以换一个方向卷一个吗?
(2) 做一做:
![]() 给2个大小一样的圆纸片和一条长方形纸带,用透明胶粘成一个立体图形,怎么粘?(长方形的长大于圆的周长)
给2个大小一样的圆纸片和一条长方形纸带,用透明胶粘成一个立体图形,怎么粘?(长方形的长大于圆的周长)
![]()
![]()
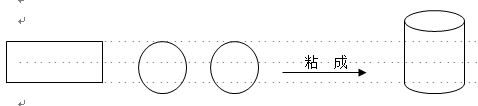
粘成
![]()
思考:圆锥的侧面展开图是什么?(扇形)
3、 生活中有很多立体图形,沿着棱剪开,能得出它的平面展开图,长方体、正方体、三棱柱、四棱锥的展开图是怎样的呢?
试一试:有一个用纸粘成的正三棱锥,用剪刀将棱DA、DB、DC剪开
(一刀两边是D1B与D2B;D3A与D1A;D3C与D2C)
![]()
沿 DA、DB、DC方向剪开 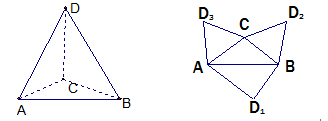
结论:沿着多面体的一些棱将它剪开,可以把多面体展开成一个平面图形。
二、实例探究并交流:
1、 如图所示的三种形状,你能想象是哪些可以折叠成多面体吗?动手做做。
(1) (2) (3)
![]()
![]()
2、 如图所示的四个平面图形,分别能折成什么立体图形?试一试。
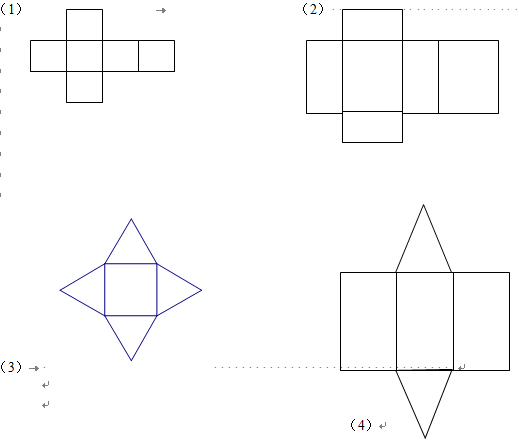
结合上面两例,联系课本理解多面体的平面展开图的意义。
常见的有三棱锥、三棱柱、四棱锥、四棱柱、长方体、正方体。
多面体的展开图可以用不同方法折叠成立体图形。常用的方法有下面两种:
(1)粘合拼凑法:找展开图外周长上共棱的边,设想用胶水粘上,看能否围成立体图形。
(2) 方位法:把有规则的平面展开图先定出上面、下面、前面、后面、左面、右面,从六个方位来思考,对长方体、正方体展开图应用比较多。
4、 如图所示的六个平面图形都是正方体的展开图吗?动手折折看。
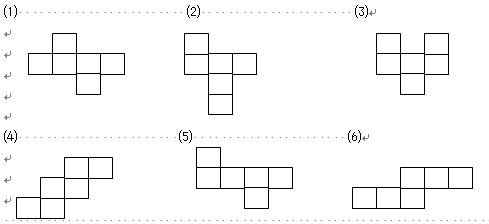
思考:你还能画出与上面不一样的正方体的展开图吗?
结论:同一个立体图形按不同的方式展开得到的平面展开图是不一样的。
5、 小组讨论完成“一、1“中的问题,多媒体演示。
三、进一步探究交流:
1、 如图是某多面体的平面展开图,指出它们的名称。

分析:左边的平面展开图,把C1、C2、C3、C4、C5合拼成一点,得到的是多面体,右边按共棱粘合方法所得出立体图形是三棱柱。

方法总结:①侧面是三角形,底面是五边形,所以它是五棱锥;
②侧面是长方形,底面是三角形,所以它是三棱柱。
2、如图不是正方体的平面展开图是( )
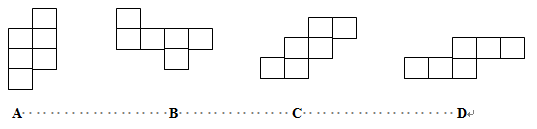
方法总结:①用方位拼凑法,B、C、D都能拼成正方体;
②一般地有田字格的不是正方体的平面展开图;
③正方体平面展开图,外周长必须是小正方形边长的14倍,简称14个单位,因为正方体剪开必须剪7刀,1刀两边,由此得出14。
四、拓展应用创新:
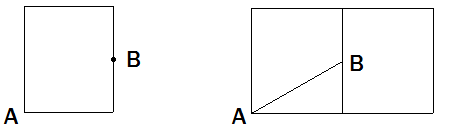
1、 建新的茶杯是圆柱形,如图是茶杯的截面图,左边下方有一只蚂蚁,从A处爬行到对面的中点B处,如果蚂蚁爬行路线最短,请画出这条最短路线图。
(点拨:画出圆柱形茶杯的侧面展开图,连结A、B两点)
2、 把立方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各个面上的颜色与花的朵数情况列表如下:
现将上述大小相同,颜色、花朵分布也完全相同的四个立方体拼成一个水平放置的长方体,如图所示。问长方体的下底面共有多少朵花?(17朵)
五、课堂小结:
1、 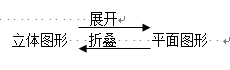
2、立体图形与平面图形相互变换的方法:
(1) 粘合拼凑法;
(2) 方位法。
设为正确答案