- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课学生已经学习了等差数列的前n项和的公式,以及等比数列的概念、性质和通项公式,知道了迭代法的思想和倒序相加法的求和方法。学生对于等比数列的求和公式推导,有了能够自我思考,进行推导的知识基础。学生能够掌握项与项之间的关系,也能够观察到如何找寻求Sn的化简方式。
1、课件ppt
2、实物投影
3、手机辅助教学
1、理解等比数列的前n项和公式的推导方法,能够运用公式解决数列求和问题。
2、提高学生的数学建模思想,体会错位相减法的方法,渗透数学分类讨论的思想。
3、培养学生的创新精神和逻辑思维能力。
教学重点:1、等比数列的前n项和公式及其应用;
2、错位相减法的方法理解。
教学难点:等比数列的前n项和的公式的不同推导方法。
1、问题探究法
2、小组讨论法
3、启发式讲授法
四、教学过程:
一、问题情境,发现新知
问题1:等比数列的定义是什么?如何用 递推公式描述?
问题2:等比数列的通项公式是什么?
问题3 :传销公司宣传海报上约定,新加入人员在第一个月(按30天)内公司每天给他1000元钱,而员工则第一天给公司返还一分,第二天给公司返还二分,即后一天返还的钱是前一天的二倍。小王想:这样的公司好呀,做一个月我就赚大了。这是一个什么数学问题?你认为小王真的赚大了?
引导分析:数学建模
每天公司给小王的钱{an}:1000 ,1000 ,1000……1000
每天小王返还公司的钱 {bn}:1 , 2 ,22 ,… … 22
S30 =1000+1000+……+1000 (元)
T30 =1+2+22 +…… +229 (分)
这是一个比较大小的问题,实质上是求等比数列前n项和的问题。
二、类比联想,解决问题
1、学生探讨: 小王一个月返还公司钱的总数是:
T30=1+2+22+·····+229 ①
上式有何特点?
如果①式两边同乘以2得: 2T30=2+22+23+···+229+230 ②
比较①、②两式,有什么关系?
2、教师总结:

三、讨论交流,延伸拓展
问题1:设等比数列{an},首项为a1,公比为q,如何求前n项和Sn。
教师引导学生由特殊到一般进行推导:
【方法一】错位相减法
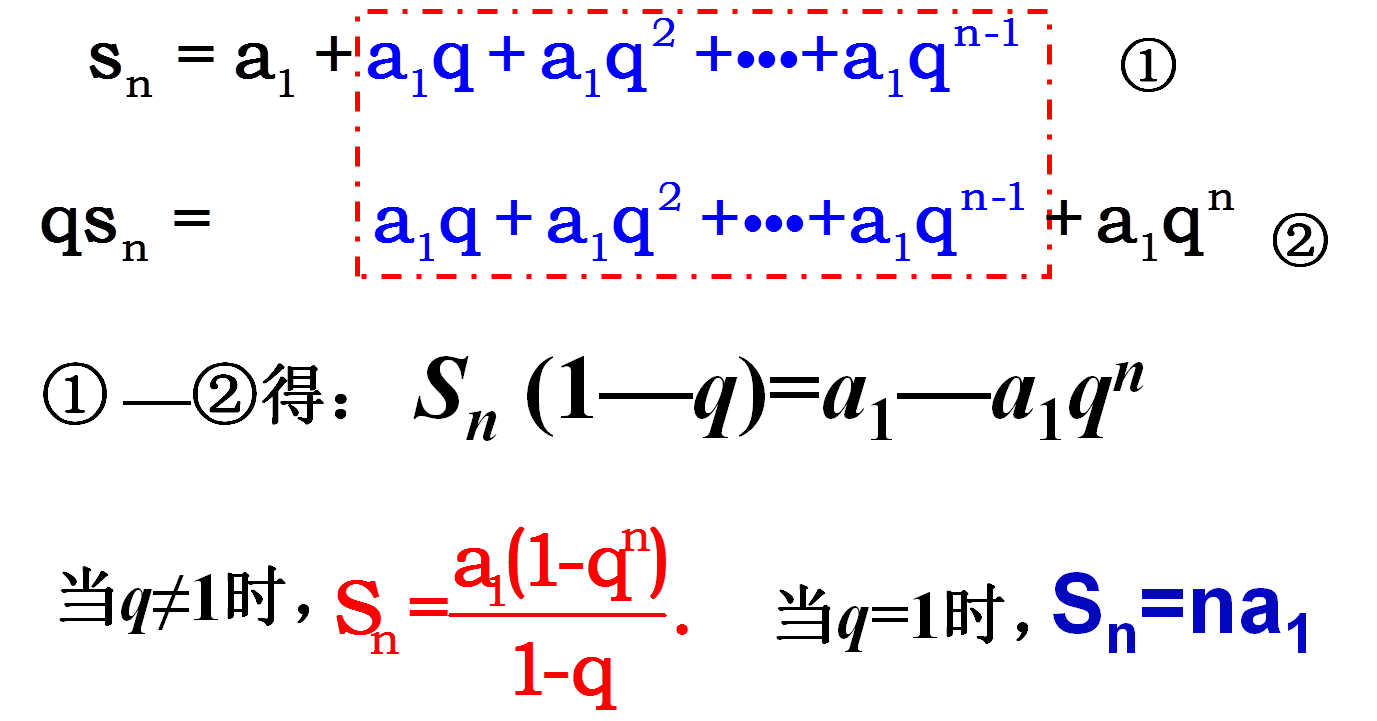
问题2:你还有其它方法推导等比数列前n项和公式吗?
1、学生分小组讨论其它推导方法。
2、教师引导分析,扩宽学生的思路:
【方法二】等比性质法![]()
![]()
1、回顾等比性质:
![]()

2、利用等比性质推导:
![]()
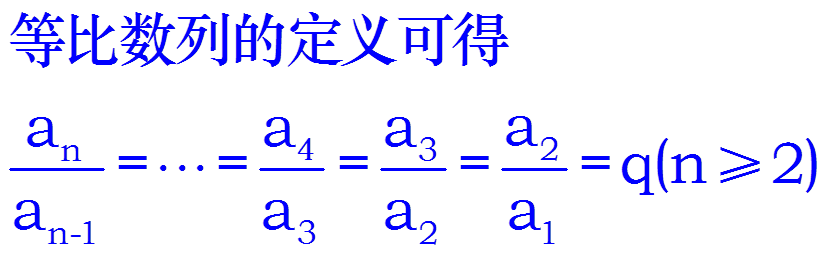
即满足:
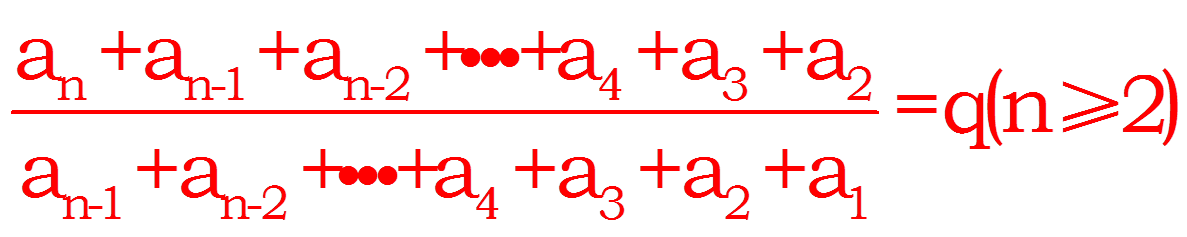
故可得:,即:
所以:
【方法三】通项公式提取公因式法:
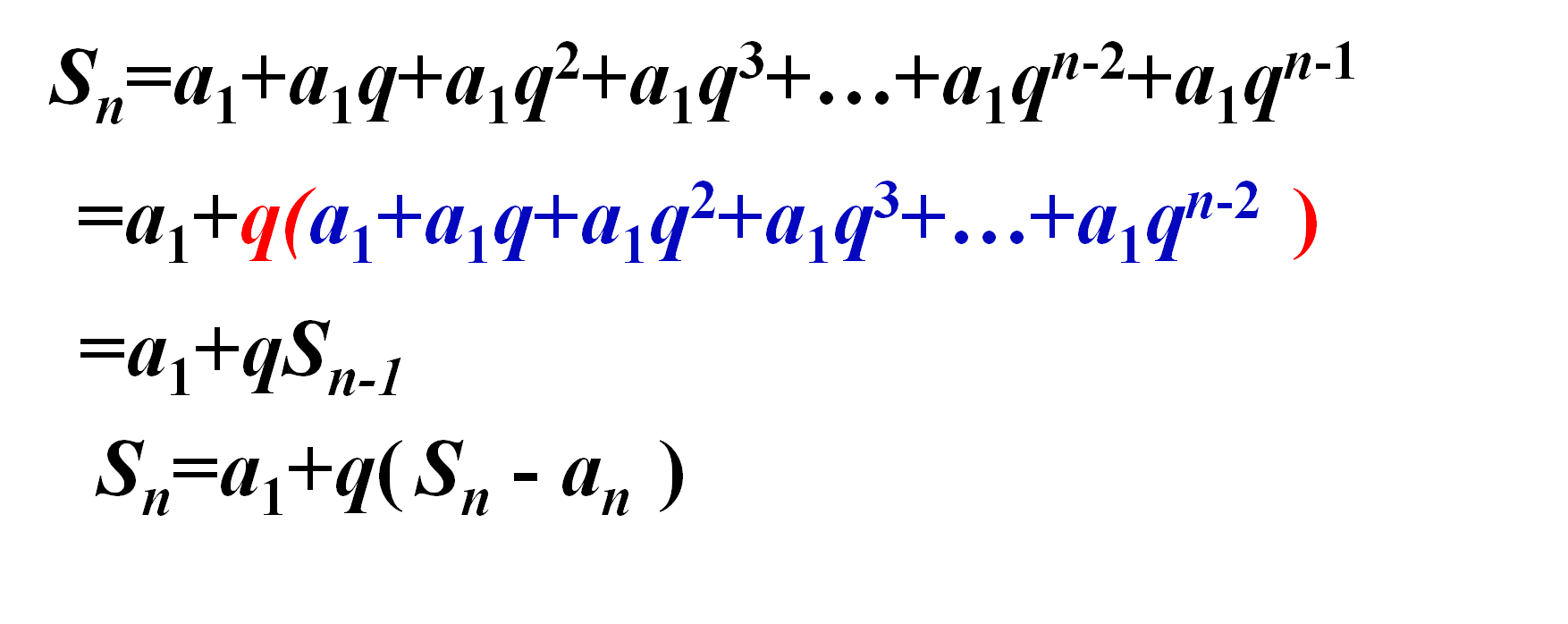
![]()
四、变式训练,深化认识
例1:等比数列 ,求它的前8项的和.
思考:若求等比数列 的前10项的和呢?前n项的和呢?
变式1:等比数列前多少项的和为
?
变式2:求等比数列 的第5项到第10项的和。


例2:求和
变式1:求
变式2:
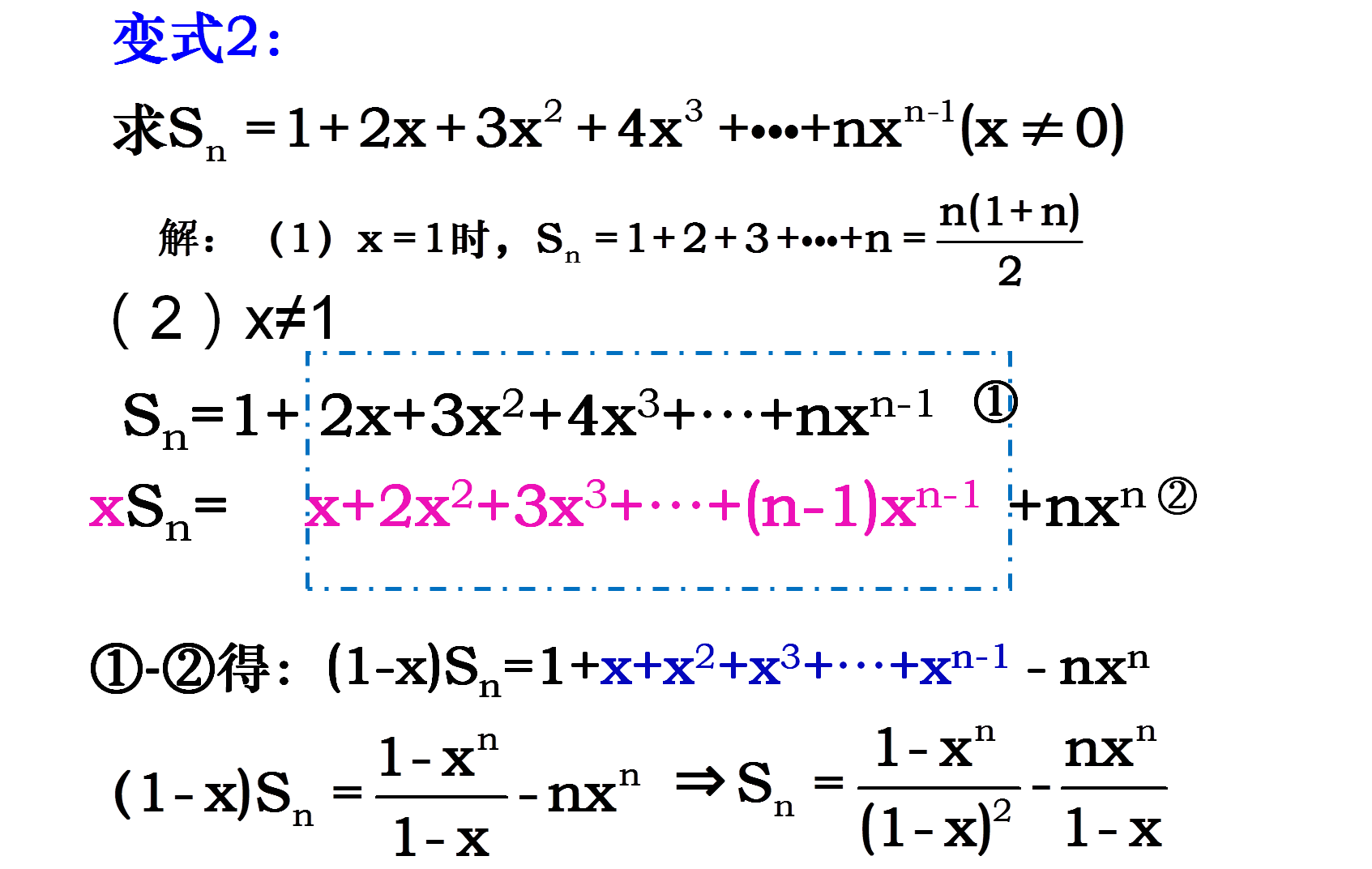
五、归纳小结,内化新知
1. “错位相减法”不仅可以推导等比数列求和公式,而且可以用来求一类特殊数列的和.
2. 是等比数列前n项和的两个基本公式,应用时一般用前一个公式.
3.等比数列的五个量中知三可求二.
六、课后作业,分层练习
1、作业:P58练习1、2.
P61习题2.5A组1.
2、课后思考:
(1) 求和:
(2)“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?” 这个问题的答案是多少?
设为正确答案