- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



六年级学生通过各阶段的学习,已经掌握了各种平面图形的面积计算方法,但因时间的关系,对推导过程有些许遗忘,并且由于对不同平面图形面积的学习是分阶段进行,因此学生对这些平面图形的面积之间并未形成联系。
PPT、公式卡片、图形卡片
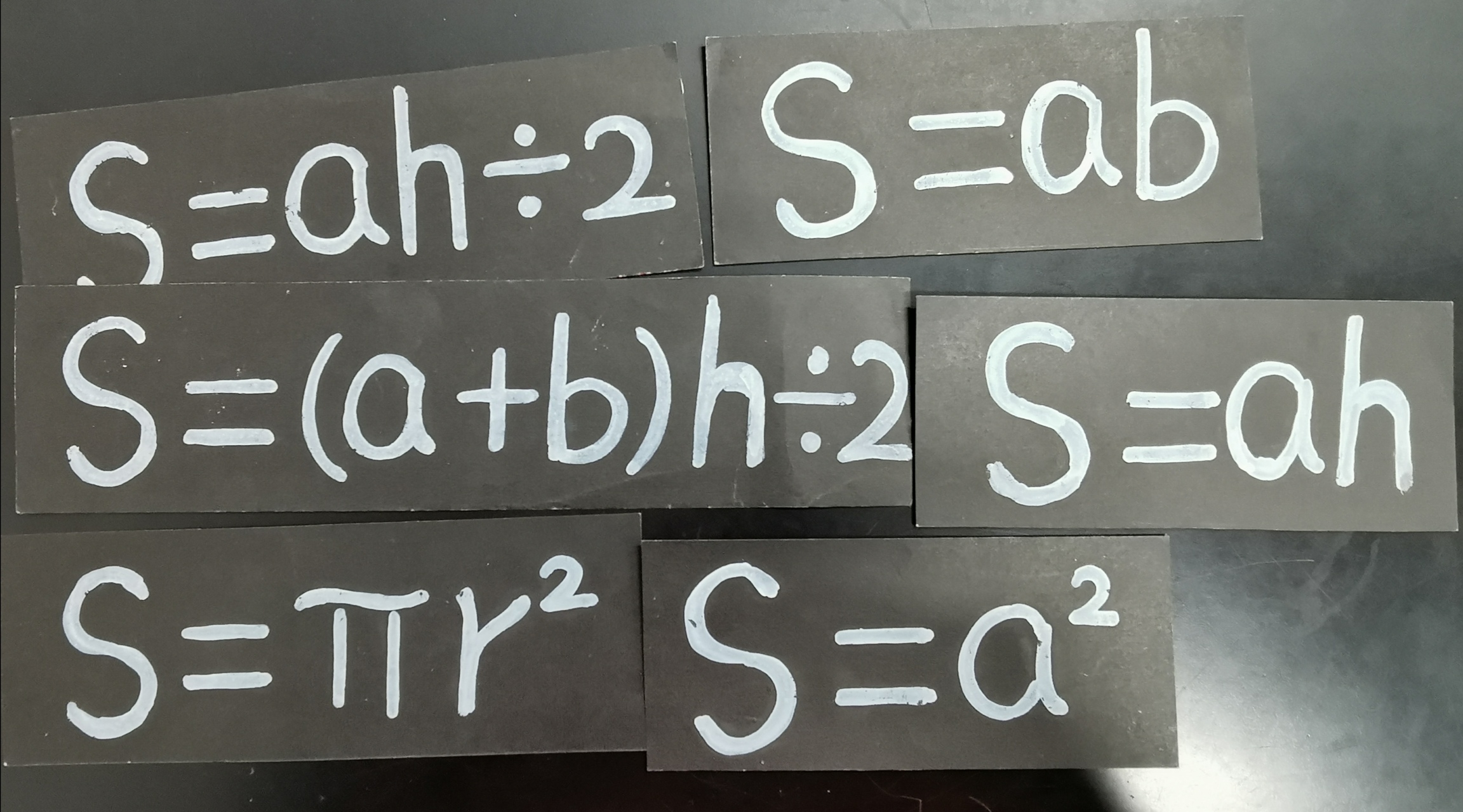

1、通过复习,回忆巩固平面图形的面积的计算公式,并巩固对公式的运用。
2、再现平面图形面积公式的推导,理清平面图形面积之间的联系,形成知识网络。
3、体验学习数学、运用数学的乐趣,培养解决问题的能力和创新意识。
1、平面图形的面积公式推导,构建知识网络。
2、理解“转化”思想,并领悟转化思想的价值。
师:同学们,今天我们要来一起复习平面图形的面积(板书课题),既然是复习面积,那我们先从面积的起源开始讲起?
1、活动一:基础巩固。
师:最早的面积相关的记载是出现在古埃及。尼罗河是古埃及文明的起源,尼罗河水流经的两岸土地肥沃,但是它每年都泛滥一次,河边的田地经过洪水的蹂躏,田界消失无踪,因此人们就需要重新丈量土地,于是逐渐有了面积的概念。(课件播放尼罗河洪水泛滥短片)
看!这是重新划分的田界,像我们学过的哪些平面图形?(课件出示田地图片)
生:长方形,正方形,平行四边形,三角形,梯形,圆。(课件出示)
师:怎样计算这些图形的面积?挑一个说说!
(学生对应说图形计算公式,黑板贴图形和公式)
师:给你这些数据,算算它们的面积吧!
师:算完了吗?自己当当小老师,快速看看算对没有?(课件出示结果)都算对的请举手告诉我!
师:真厉害!看来大家对面积的计算都掌握的很好!
2、活动二 :回顾公式推导,感受转化的思维方法。
(1)师:我们已经学习了这么多平面图形的面积公式,不妨我们一起来回顾一下之前的学习历程,也许在回顾中你会有更多新的发现哦!
(2)师:一开始我们肯定是不知道这些图形的面积公式的。谁还记得最先我们学的是哪种图形?
生:长方形。
师:长方形的面积公式我们是怎么得到的?还记得吗?
预设一:生:用小方块去量。
师:怎样的小方块?(无论学生怎么回答)是单位面积的小方块,像度量重量、长度有它们的单位,度量面积也要先确定它的面积单位。黑板上这样大的就是单位面积是1平方分米的小方块。(黑板右上角贴小方块)我们当时就是用这样的小方块当成学习工具去量的。(课件演示)
预设二:无人回答
师:其实要知道面积,首先我们确定了面积单位。(黑板上贴小方块)想起来了吗?
生:我们是用这样的小方块去量的。
师:没错,当时我们就是这样……(拿小方块在长方形上比划)用单位面积的小方块去量的。(课件演示)
师:那这样量最后公式为什么是长乘宽呢?
生:长是多少一行就摆几个,宽是多少就摆几行,长乘宽得多少就意味着摆多少个面积单位,所以长方形的面积是长乘宽。(结合课件演示描述)
(若无学生回答,师:在这个面积公式里长表示什么?宽表示什么?)
师:通过用面积单位作为工具去量我们得到了长方形面积公式(将长方形移动到黑板的右边),后面的学习中我们就可以直接用公式算出长方形的面积。
(3)正方形
师:那正方形师特殊的长方形,顺理成章我们同时得到了正方形的面积公式。
(移动到右边)
(4)平行四边形
师:接下来我们学了什么?
生:平行四边形。
师:没错,你还记得它的面积公式的推导过程吗?
生:剪拼变成长方形。/把平行四边形的一边剪开拼在另一边,变成长方形。(可以让学生拿着平行四边形边比划边说)
师:我喜欢刚才他提到的一个词,“变成”, “变成”其实就是数学里的转化!将平行四边形转化成长方形。
师:长方形是在平行四边形之前已经学过了的,通过转化的方法我们就把已知的图形面积公式作为工具推导出平行四边形的面积公式。在学习长方形的时候我们是用单位面积的小方块去量的,那平行四边形可以也利用小方块去量吗?
生:可以。
师:咱们来试试。(课件演示)
这儿不足一块……按半块算。只是这样的方法比较麻烦,而且不太精确,所以我们选择利用长方形这个工具来推导更方便一些。
(5)三角形和梯形
师:三角形和梯形能转化成什么图形?
生:用2个完全相同的三角形拼成1个平行四边形。/用2个完全相同的梯形拼成1个平行四边形。
师:是的,当时我们就是转化成了平行四边形,把它作为工具推导出三角形和梯形的面积公式的。那之前我们有了这么多工具(手指黑板右边所贴小方块和图形)。除了平行四边形,我们是不是也可以用其他的工具(手画圈指黑板上的面积单位和长方形)来得到三角形的面积呢?想一想!
生:(犹豫)
师:用小方块去量或者变成长方形可以吗?
生1:可以用小方块去摆,和平行四边形一样,不足1块算半块。
生2:把三角形……变成长方形。(若无学生回答,师:其实变成长方形也是可以的,看!课件演示 长方形的长是三角形的底,宽是三角形高的一半,公式中的除以2就体现在这里。梯形是不是也可以这样变?)
师:前面学习的知识原来都可以当做工具来解决三角形和梯形的面积问题。(三角形\梯形移到黑板右边)
既然都可以,那为什么之前学习的时候书上主要介绍了转化成平行四边形的方法呢?
生:简单些。
师:是的,虽然可利用的工具很多,但目的相同,方法当然越简单越好 。所以书上选择了最简单、最容易理解的办法。
(6)圆
师:最后我们学习了什么图形 ?
生:圆。
师:现在我们已经有这么多工具了(手指黑板右边),我们可以转化成这些我们学过的图形计算它的面积吗? 你想转化成哪一种?
生:平行四边形/长方形。
师:其他的工具可不可以?
生:可以。
师:能分享一下你的想法吗?
生:
师:其实,关于圆的面积计算公式古希腊数学家就利用三角形这个工具推导出来了,看!(课件演示)
师:老师这里还有一种利用三角形这个工具的方法哦。(课件演示)
师:那如果分成12份,还是这样去摞,就拼成了……类似梯形的图形。
(7)师:利用前面的工具我们得到了圆的面积公式。(圆移到黑板右边)
随着学习历程的推进,瞧!我们的工具越来越多。我们以后再遇到新的图形时,这些工具都可以用来帮助我们解决问题。只是当我们遇到新的问题时,这些工具都要使用吗?
生:不是。
师:对,当我们遇到新的问题时,究竟该选择哪些工具,就要视具体情况而定了。
活动三:纵向迁移,体会面积公式间的联系。
师:学习了这么多面积的公式,有个同学告诉我:我们只要掌握了一种图形的面积公式,就能记住所有图形的面积公式。你认为呢?(等待学生思考十来秒)
生:我觉得可以。
生:我觉得记住长方形的面积公式就可以了。
师:说说你的想法。
生:长方形的面积公式可以推导出其他图形的面积公式,它是基础。
师:真会思考!但这个同学说的是记住梯形的面积公式就可以了。(黑板单独拉出梯形面积)
生:(疑惑/怀疑)
师:怀疑?老师这里又一个梯形,这个梯形它是可以变化的,接下来我们就利用它来帮助研究。(课件)想不想看看它会怎样变成三角形?
生:想!
师:仔细观察,变化后的图形与梯形有什么关系!
(课件演示梯形上底缩短变成一个点)
生:我发现这些图形的底和高没有变。
生:我发现梯形上底逐渐变短了,最后梯形变成了三角形。
师:图形是这样变的,公式是怎样变的?
(板书:S三角形=(0+a)h÷2=ah÷2)
生:(惊讶)
师:换个角度,请看!(课件演示梯形上底变长)可能会变成……
生:上底和下底相等,变成平行四边形。
生:如果两腰和底成直角,就变成长方形。
生:如果腰和底不只成直角,还相等,就变成正方形。
师:多清晰的思路!图形发生了变化,公式发生了怎样的变化呢?请看。
(板书:S平行四边形=(a+a)h÷2=ah
S长方形=(a+a)b÷2=ab
S正方形=(a+a)a÷2=a2)
师:想不想看看梯形继续变下去,是怎样变成圆的?
生:想!
师:不过,有个特殊要求,观察时,请大家牢牢盯住梯形的上底和下底,看变化的过程中,上底和下底变成了圆的什么?
生:上底和下底的和变成了圆周长。
(板书:S圆=(πr+πr)r÷2=πr 2)
师:神奇吗?
生:神奇!
师:正是因为这些图形之间神奇又亲密的关系,我们才能把它们当做工具来互相推导面积公式。
现在老师这里有一个新图形,你能利用这些工具计算它的面积吗?计算它的面积你需要那些数据?
不要急回答,老师给大家提供了一些材料,同桌可以合作,将你们的想法呈现在学习单上。现在开始吧!
设为正确答案