- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



在本节活动课开展之前,学生已经学习了二次函数的意义,理解了其图象及性质,并能解决简单的实际问题。但建立二次函数模型解决问题对于学生来说本就是一个难点,加上一直以来教师在教学中对数学活动课重视程度不够,学生动手动脑探究能力亟待提高,本节课学生在探究时遇到的阻力很可能会比较大,那么应当注重对学生的问题引导、适时指导,同时给学生充分自主探究的时间.
多媒体课件(含PPT课件、几何画板课件)、计算器、希沃授课助手
[知识与技能]:
1、探究具有某种特点的两数的积中存在的某种规律以及动点的轨迹问题;
2、能建立二次函数的模型说明猜想的正确。
[过程与方法]:
1、经历实际操作,进行猜想与推理的过程;
2、体验数学建模思想,数形结合思想;
3、体会由简单到复杂,特殊到一般的数学思想方法。
[情感态度与价值观]:
1、鼓励学生积极参与数学活动,培养学生的观察、猜想、推理、归纳和概括能力;
2、采用自主探究和小组合作交流相结合,培养学生独立思考能力和合作意识;
3、在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心。
教学重点:
探究具有某种特点的两数的积中存在的某种规律,建立二次函数的模型说明猜想的正确。
教学难点:
建模
本课采用教师引导和学生自主探究相结合的教学方法。教师在学生思维出现“坎”的地方适当引导启发,学生通过动手实际操作、独立思考而后小组合作交流来解决问题。
师:同学们知道世界三大数学猜想吗?世界三大数学猜想即费马猜想、四色猜想和哥德巴赫猜想。我们先来通过一个短片了解一下其中的四色猜想。(播放短视频《四色猜想》)
从这个短视频中我们可以初步感受到:数学猜想有着重要的意义,它是推动数学理念发展的强大动力。它能够强烈地吸引数学家全身心投入,积极开展相关研究,数学猜想一旦被证实,就将转化为定理,丰富数学理论。今天,我们也将通过参加两个数学活动,体会猜想的魅力,同时学会建立二次函数模型解决具体数学问题。(出示课题)
活动一、关于两数乘积的猜想与证明
(投影)观察下列两个三位数的积,猜想其中哪个积最大.
901×999,902×998,…,998×902,999×901.
问题引导:
(1) 猜想的前提是仔细观察。 这些计算式有怎样的规律?
(2) 你的猜想是怎样的?为什么会这样猜想?(学生自由发言,教师肯定学生的积极思考,不一定要对学生的答案予以肯定或否定评价。)
(教师适时引导)我们研究较复杂的数学问题,可从简单情况着手。先研究稍小一点的数,算一算,看你的猜想是否正确:
①计算:1×9,2×8,3×7,4×6,5×5,6×4,7×3,8×2,9×1。找出其中积最大的。
②计算下列两个两位数的积,其中哪个积最大?
91×99,92×98,…,98×92,99×91.
(3) 有了猜想,我们如何进行证明?
(学生尝试独立完成,然后小组合作交流讨论。教师巡视指导,根据情况点名上台板演,如果有不同思路的,则可帮助学生利用希沃授课助手进行展示讲解。)
证明:设第一个数是900+x,则第二个数是(1000-x), 设两数积为y.
(1)求y与x的函数关系式;
y=(900+x)(1000-x)=-x2+100x+900000
(2)求y的最大值;
y=-(x-50)2+902500
∴y的最大值为902500,此时x=50.即950×950最大.
师:活动一的探究告诉我们可以通过建立二次函数模型解决求最大值的问题,也体会到了由简单到复杂的的思想方法。下面我们再通过
活动二进一步体会猜想和建模的魅力。
活动二、曲线L的形状
如图,在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成以下作图步骤:
① 连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1,l2的交点为P.
② 在x轴上多次改变点M的位置,用①的方法得到相应的点P,把这些点用平滑的曲线连接起来.
 |
(学生动手实际操作,经历作图过程,初步感知和猜想,教师通过希沃授课助手展示几个学生的作图;然后,教师用几何画板动态演示。)
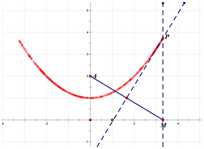
(1) 观察画出的曲线L,猜想它是我们学过的哪种曲线?
(抛物线)
(2) 由刚才的实际操作我们可以发现曲线L是一条抛物线。如何进行推理说明猜想的正确性呢?
(给予学生充分的自主探究时间:先独立思考,然后小组合作交流。教师巡视指导,关注学生是否能建立二次函数模型解决问题。)
如果学生遇到困难,教师可以适当引导。
问:①要说明点P的运动轨迹是一条抛物线,只需要说明点P的纵坐标与横坐标之间存在什么关系?
②对于曲线L上任意一点P,线段PA与PM有什么关系?设点P的坐标是(x,y),你能由PA与PM的关系得到x、y满足的关系式吗?
(具体解答过程可依情况由小组派代表上台来讲析,可借助希沃授课助手展示其解答过程。)
解:对于曲线L上任意一点P,连接PM、PA, 则线段PA与线段PM的关系为:PA=PM,
设点P的坐标为(x,y),
则PA2=x2+(y-2)2,PM=|y|,由PA与PM的关系列等式x2+(y-2)2=y2,
化简得y=x2/4+1.
由此,点P在函数y=x2/4+1的图象上.
即曲线L的形状是抛物线.
小结:通过活动二我们建立二次函数模型解决了动点轨迹是抛物线的问题,从中也体会到了数形结合思想。
补充“数海拾贝”:著名数学家华罗庚说过:“数与形,本是相倚依,焉能分作两边飞。数缺形时少直觉,形缺数时难入微。数形结合百般好,隔裂分家万事非。切莫忘,几何代数统一体,永远联系莫分离。”
1、学生自我评价与反思:这节课你有什么收获?有哪些不足?
(提示学生可从知识、能力、方法、情感体验等方面自由谈,同时教师关注学生是否能总结建模思想、数形结合思想、由简单到复杂的思想方法等,及时补充。)
2、教师对学生评价:学生的活动过程中回答问题、参与小组合作交流等方面进行评价。
仿照活动一根据某种规律自行编题,先猜想最大(小)值,然后通过建模进行推理验证。
设为正确答案