- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
六年级大部分孩子对数学学习的积极性比较高，能从已有的知识和经验出发获取知识，抽象思维水平有了一定的发展。基础知识掌握比较牢固，有一定的学习数学的能力，大部分学生学习态度端正，学习习惯较好，空间观念较强，上课时能积极思考，能够主动，创造性地进行学习。对于《一笔画》的知识，孩子们有一定的知识经验，因此说出它的概念没有难度，本节课的重点就在于在实践探究中得到判断一个图形能否一笔画的方法，让学生在思维中操作，在操作中思维。激发学生的学习兴趣，培养学生的创新能力和应用意识。
探究学习单、投影仪、课件
让学生充分体验一笔画的画法，会找解决问题的关键点，在探究活动中，进一步得到判断一个图形（连通图）能否一笔画成的方法，激发学生的学习兴趣，培养学生归纳概括和解决问题的能力。
学生在实践探究中得到判断一个图形能否一笔画的方法。
合作探究
课前提前玩5分钟的游戏：兔子吃胡萝卜（电脑已下载app:patchmania），喊学生上台体验、过关。
提问：要想成功过关，最关键的是什么？生：把所有的胡萝卜连成一条线，一笔画成。对，这就蕴含了数学知识——一笔画。这节课我们就来学习一笔画的知识。
一、学生提问
看到“一笔画”。你能提出什么数学问题？
问题1：什么是一笔画？（很好，我们在研究一个新问题时，首先得搞清楚这是什么。）
问题2：是不是所有的图形都能一笔画？
问题3：是否能一笔画与什么有关？（你这个问题很重要。）
问题4：什么样的图形能一笔画？（非常好，你抓住了研究问题的关键：能一笔画的图形有什么特征）
问题5：能一笔画的图形，怎样画？
问题6：学一笔画有什么用？
…
真不错，我们班的孩子很会提问题，会提问题的孩子数学一定学得很好。现在我们就开动脑筋，一个一个地解决这些问题。
二、解决问题
1、解决问题1。
师：你认为什么是一笔画？
生：如果一个图形能够一笔画出，简称一笔画。这里的“一笔”，有什么具体要求？（ⅰ）连续不断（ⅱ）不重复。老师顺势在黑板上画一个图形
。注：这里指的重复，意思是线不能重复，一个点是可以重复的。
2、解决问题2。
师：是不是所有的图形都能一笔画？
生：有的图形不能一笔画，比如说断开的图形：
。就算图形是连起来了的，也不一定能一笔画，例如…。（如果学生举例不出，老师可以提一句：我们等一会儿会看到这样的图形。或者在黑板上画一个图形：
）
3、解决问题3
师：一笔画与什么有关？你们大胆地猜猜看。生1：点。生2：线。你们很有想法。一笔画与点和线到底有什么联系呢？这个问题很重要，待会儿我们要花比较多的时间来研究这个问题。
4、解决问题4和问题5
（1）现在我们来研究一笔画的特征。说起特征，我们并不陌生，回忆一下，在哪里研究过什么的特征呢？比如说5的倍数特征。还记得当时是怎么研究的吗？我们写了很多的5的倍数，再观察，找规律，发现5的倍数个位上都是0或者5.这个研究方法在这里也同样适用。首先我们要找出很多的图形（课件出示七个图形），接下来要做什么呢？生：要找出哪些是可以一笔画的，再观察它们的共同点，找出它们的特征。
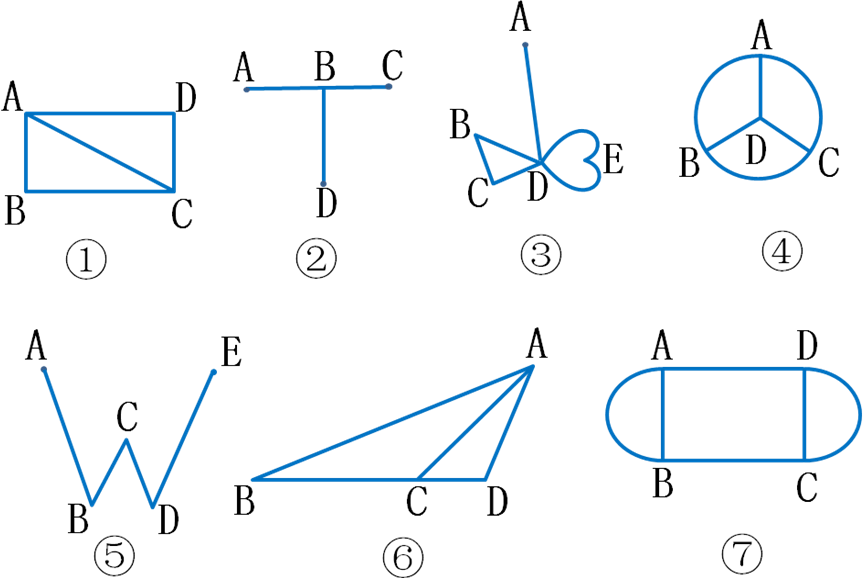
出示学习单：（ⅰ）下面哪些图形可以一笔画？可以请打√，不可以打×。
（2）小组合作探究。我们先来看第一个图形
，它能一笔画出吗？学生1上台指一指怎么画，老师板书路线：ACCBBAADDC。还有不同的画法吗？学生2上台指一指，教师板书路径ADDCCBBAAC。从C出发可以吗？可以学生3在座位上说，教师板书路径CDDAABBCCA。这三个同学的方法各不相同，但是也有相同的地方，你们看出来了吗？生：起点都是A和C。以B为起点可以吗？不可以。也就是说，只能以A、C点作为起点和终点。以其它点作为起点，都不能一笔画成。（其他的图形留给大家研究。）
（ⅱ）如果图形可以一笔画，请写出它的路线，用红笔标好起点和终点，并和同桌讨论：为什么选择这些点作为起点和终点？它们有什么特别之处？
同桌两人为一组，尽快完成。
学生汇报问题1：可以一笔画的有图形有：①、③、⑤、⑥；不可以一笔画的图形是②、④、⑦。
学生汇报图①、③、⑤、⑥的路线，老师在图上指一指。下面的同学有没有选其他的点作为起点和终点的？为什么你们都不约而同地选择了这些点作为起点和终点呢？它们有什么特别之处？引导学生说出：这些点引出的线的条数都是奇数。我们给这种点取个名字，叫作：奇点。这几个图形都有2个奇点。我们在一笔画的时候，都是从一个奇点出发，到另一个奇点结束。
有奇点，就还会有？偶点。你认为什么是偶点？从一点引出的线的条数都是偶数，这个点就称为偶点。（图中剩下的点都是偶点。）
这里还有很多不一样的图形，它们都可以一笔画，因为时间的关系，我们就不一一进行研究。这些图形都有2个奇点。画的时候都是从一个奇点出发，到另一个奇点结束。
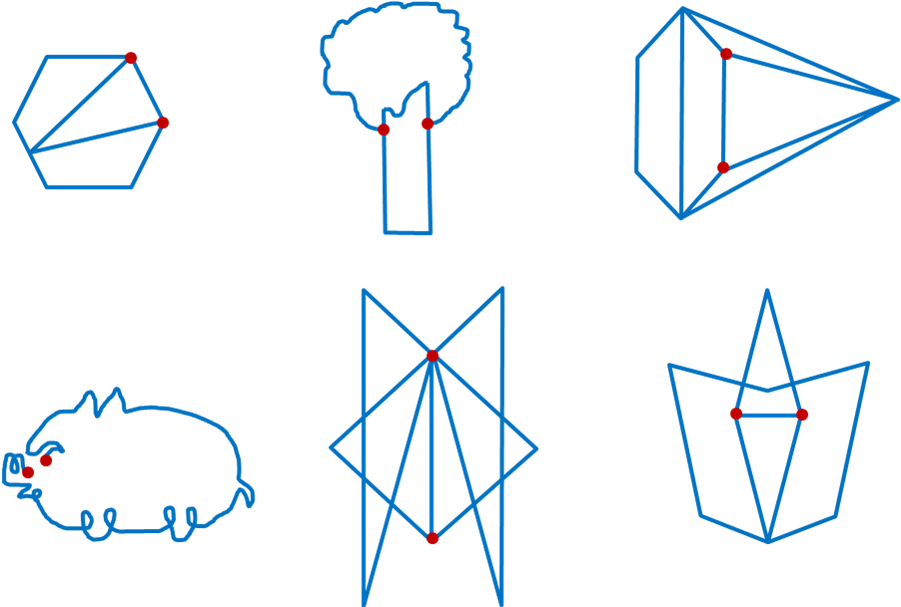
师：是不是所有可以一笔画的图形都有这样的两个奇点呢？猜猜看。生：不一定吧。要想解答这个问题，我们可以用什么方法？生：举例试一试就知道了。是的，举例是一种很好的办法。请每个同学画2-3个可以一笔画的图形，写出奇点的个数，并标出起点和终点。
师：在你画出的图形中，有两个奇点的，请举手。
师：除了有2个奇点的，还有别的情况吗？有。学生上台用投影仪展示。
师：请介绍一下你的图形。
生1：我画的是长方形，没有奇点，从某一点出发，最后又回到了这个点。老师：我可以换一个起点吗？可以。
生2：我画的是五角星，没有奇点，从某一点出发，最后又回到了这个点。这个图形能换起点吗？能。任意一点都可以作为起点。
师：这两个同学画的图形都没有奇点，换句话说，只有偶点。画图的方法都是从一个点出发，最后又回到了这个点（起点和终点重合）。（板书：0个奇点）
师：我们班画出了奇点个数为0和2的图形，还有别的情况吗？生：没有了。
看来，一笔画与奇点的个数有密切的关系。当奇点个数是0或2时，是可以一笔画的。从你们画的图来看，只有这两种情况。
（3）研究不能一笔画的图形
我们再来看看不能一笔画的图形，它们是②、④、⑦，仔细观察，这三个图形点线之间的关系与其他图形有什么不同？这三个图形有4个奇点。看来呀，有4个奇点的图形是不能一笔画出的。想想看：4个奇点的图形一笔不能画成，那要几笔才能画成呢？生：两笔。也许有的图形两笔也画不成，需要3笔、4笔甚至更多，这就是以后要研究的几笔画问题了。
1、介绍欧拉：这节课我们利用分类、类比、举例等方法研究了一笔画，发现了什么规律？生：当奇点个数为0或者2时，可以一笔画。真了不起，你们的发现跟一位数学家的发现是一样的。这个伟大的数学家就是——欧拉。欧拉13岁就进巴塞尔大学读书，如今几乎每一个数学领域都可以看到欧拉的名字，很多成果都是以他的名字命名的，如：欧拉线，欧拉定理，欧拉方程，欧拉函数，欧拉公式等等，他的成果多到数也数不清。
指一指黑板上板书的路线ACCBBAADDC，这种记法就是欧拉的记法，看起来有点麻烦，但实际上是一种非常好的记法。好在哪里呢？刚刚有同学发现了：中间这些点成对出现，只有起点和终点特殊，是单着的，于是欧拉给这两个点取了个名字，叫作奇点。
欧拉为什么要研究一笔画问题呢？原因要从一个故事讲起：在18世纪，人们遇到了一个难题“七桥问题”，当时无人能解答，直到数学家欧拉用一笔画的知识解决了这个问题。
2、七桥问题
一座城市，中间有一条河穿过，河上有两个小岛，有七座桥把两个岛与河岸联系起来，有人提出一个问题：一个步行者怎样才能做到不重复、不遗漏地一次走完七座桥？
人们关心的是能不能不重复、不遗漏地一次走完这七座桥，而并不关心岛的大小和桥的长短，因此我们可以用4个点来表示小岛和岸。用七条线段表示七座桥。现在这个问题就转化成了我们今天学的一笔画问题了。你认为步行者可以做到不重复、不遗漏地走完七座桥吗？
生：不行，因为图中有4个奇点，不满足可以一笔画的条件。
（你会用今天学的知识来解决问题，很棒！）
如果让你当一回设计师，在此基数上进行二期改造，你能否设计出不重复一次走完全程的图呢？
生1：拆掉一座桥（AD之间的桥）。
生2：建一座桥（连接AB或AC）。
我们班的孩子很聪明。你们知道吗，“七桥问题”在当时是一个世界难题呢，无人能解答，直到著名数学家欧拉用一笔画的知识才解决了这个问题。欧拉一生有很多成就，也有很多值得我们学习的地方，由于时间关系，就不跟大家一一介绍，大家回家可以查查相关资料。
这节课我们学习了一笔画的有关知识，通过探索，有了很多的成果。关于“一笔画”，你还有什么问题吗？
生：有没有奇点为3个的情况？
生：奇点的个数如果大于4，又会出现什么情况？
设为正确答案
