- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



高一学生已经学习了函数的基本概念、指数函数、对数函数、幂函数,对函数的图像与性质有了比较系统的理解。也已经学习指数函数、对数函数、幂函数的图形与性质,但是对于形如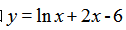 的函数还不熟悉。另外,刚进入高中,学生的动手,思考能力,观察、归纳能力都还不够,在本节课的学习上还是会遇到比较多的困难。所以在本节课的教学过程中,采用问题驱动教学,老师为主导,让同学更多的参与到课堂,在实践探索中归纳总结出零点存在性定理。
的函数还不熟悉。另外,刚进入高中,学生的动手,思考能力,观察、归纳能力都还不够,在本节课的学习上还是会遇到比较多的困难。所以在本节课的教学过程中,采用问题驱动教学,老师为主导,让同学更多的参与到课堂,在实践探索中归纳总结出零点存在性定理。
PPT、手机、播放笔、手机一体机同屏系统、希沃授课助手、希沃白板
知识与技能:
1、正确理解函数的零点与方程的解间的关系,能利用函数图象求零点或者判断方程根的个数;
2、掌握零点存在性定理,并能利用零点存在性定理判断零点所在区间及其个数。
过程与方程:
1、从研究具体一元二次函数到一般一元二次函数再到一般函数,让学生经历“类比-归纳-应用”的过程,从具体到抽象,从特殊到一般;
2、在函数与方程的联系中体验数形结合思想和转化思想,体会函数与方程思想;
3、通过知识的构建,培养学生数学抽象、逻辑推理、直观想象、数学运算等数学核心素养。
情感态度价值观:
1、通过观看《中国历史上的方程求解》,经历数学方程发展的过程,感受数学的乐趣,培养对数学的热爱和认同感;
2、通过对零点存在性定理的研究,培养学生认真、耐心、严谨的数学品质;
3、让学生在解决问题的过程中,体验成功的喜悦。
重点:了解函数零点的概念,体会函数的零点与方程的解之间的联系,掌握函数零点的判断。
难点:认识零点的概念,探究发现零点存在性定理,体会到零点存在性定理的充分非必要性,能利用适当的方法判断零点的存在或确定零点。
采用问题驱动教学、老师引导与学生讨论相结合的教学方法。
四、教学过程:
(一)知识引入
观看《中国历史上的方程求解》视频。
设计意图:学科交融,从中国历史上方程的发展过程,让学生感受数学的发展过程,引发学生数学学习兴趣。
(二)观察归纳,得出概念
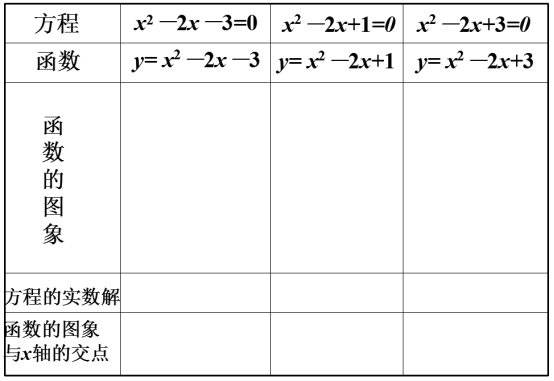
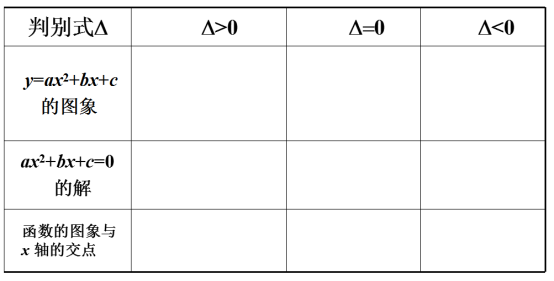
思考探究一:观察几个具体一元二次方程及其相应的函数图象,根据函数图像写出对应方程的解。
思考:函数图象与x轴交点与对于方程的解有什么关系?


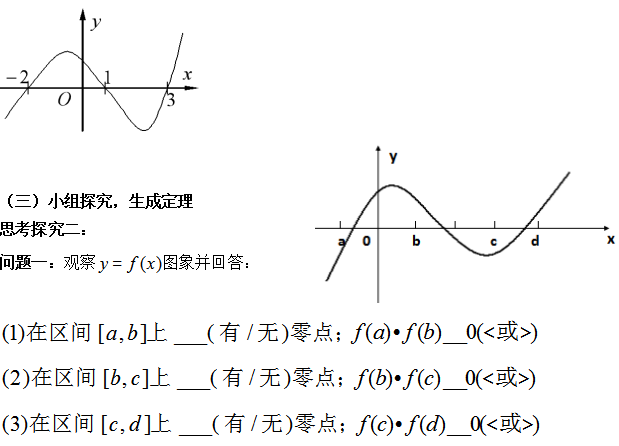



(六)课堂小结,升华内涵
一. 知识和要求:
1、通过函数图像___零点;
2、通过方程___零点;
3、通过零点存在定理___零点;
4、求方程的根的问题转化为_______________。
二.数学思想方法:函数与方程的思想、数形结合的思想、转化与化归的思想、特殊到一般的思想。
[作业] 1、教材P144 练习1、2
2、预习4.5.2
[板书设计]
函数的零点与方程的解
一、函数的零点 等价关系:
二、零点存在定理
设为正确答案