- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



小学数学中已接触过三角形的三角形、顶点、边、角、等腰三角形、底边、顶角、底角的定义,虽然学生对这部分新知识并不感到陌生,但有必要进一步学习,注意这些与中学知识的衔接,把他们小学学过的偏重于感性知识的知识加以系统化,并在理论上加以证明或说明。通过动手实践与操作,指导学生通过折叠等数学活动发现等腰三角形的性质,注重知识的探究过程。
等腰三角形三角板(加了铅垂线)、不同角度的彩色硬纸片等腰三角形
1.引导学生学习并掌握等腰三角形的性质,会运用等腰三角形性质解决有关问题。
2.引导学生掌握等边三角形的性质,会运用等边三角形的性质解决有关问题。
3.通过提出问题,引导学生根据问题归纳等腰三角形的概念,进而学习等腰三角形的性质及运用。
4.培养学生发现观察分析问题的能力,发展学生科学探究的精神。
5.通过数学知识与生活实际的联系,引导学生体会“数学来源于生活,又服务于生活”的情感,提升学生学习数学的兴趣。
重点:等腰三角形的性质及运用;等边三角形的性质及运用。
难点:等腰三角形“三线合一”的性质的理解及其运用。
从画图、拼图入手,通过教具演示,启发学生探索、猜想,直到最后论证。
1、美图欣赏:欣赏益阳西流湾大桥照片,找到其中的几何图形——等腰三角形,从而发现生活处处充满数学元素。
2、抛出问题:自制教具演示其作用,在等腰三角形三角板底边的中点加一条铅垂线,当绳子恰好经过三角形的顶点时,即可判断黑板是否水平。抛出问题:为什么加了这样一条绳子的等腰三角形就具有了这样的功能?这根绳子又代表了什么特殊的线段?引起学生好奇,激发学习兴趣,引出课题。
一、自学自研(观察发现,得出性质)
自主阅读书本P61-63页,完成下列问题。
1.活动:请同学们动手折一折手中的等腰三角形,观察其中重合的角和线段,有何发现?试猜想等腰三角形的性质并完成下列问题。
作△ABC 关于顶角平分线AD所在直线的轴反射,由于∠1=∠2,AB=AC,因此:
(1) 射线AB的像是射线AC,射线AC的像是射线 ;
线段AB的像是线段AC,线段AC的像是线段 ;
点B的像是点C,点C的像是点 ;
线段BC的像是线段CB.
从而等腰△ABC关于直线 对称.是 图形,
对称轴是 所在的直线。
(2) 由于点D的像是点D,因此线段DB的像是线段 ,
从而DB DC,AD是底边BC上的 .
(3) 由于射线DB的像是射线DC,射线DA的像是射线 ,
因此∠BDA ∠CDA= °, 从而AD是底边BC上的 .
从而AD既是△ABC的顶角平分线,又是底边上的 ,还是 。
(4) 由于射线BA的像是射线CA,射线BC的像是射线 ,
因此∠B ∠C.
由此我们得到三角形的性质定理
由(1)我们可以得出:
等腰三角形是 图形,对称轴是 所在的直线.
由(2)(3)我们可以得出:
等腰三角形底边上的 、 及 重合(简称为“三线合一”).
由(4)我们可以得出:
等腰三角形的 相等( 简称“等边对等角”).
2.尝试用几何语言表示上述性质:

练一练:如图,在△ABC中,AB=AC,AD为BC边上的高,∠BAC=49°,BC= 4,求∠BAD的度数及DC的长.
解:∵AB=AC,AD为BC边上的高
∴∠BAD= ;
DC= ;
依据 。
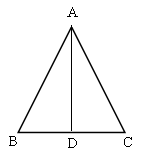
3.如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
因为△ABC是等边三角形,
所以AB=AC=BC,
从而 ( )
由 可得:
∠A=∠B=∠C= °. 
由此我们可以得到等边三角形的性质:
等边三角形的三个内角 ,且都等于 °。
并且,等边三角形的特殊的等腰三角形,所以等边三角形也是 图形,有 条对称轴,对称轴是 所在的直线。
二、合作共研(等腰三角形性质(三线合一)的应用)
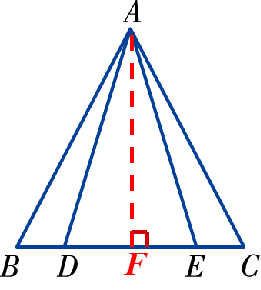
1 已知:如图,在△ABC中,AB=AC,点D、E在边BC上,且AD=AE.
求证:BD=CE
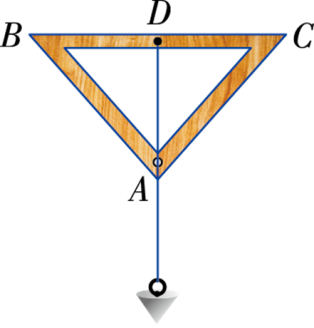
2.如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在铅锤线上.
(1)AD与BC是否垂直,试说明理由.
(2)这时BC处于水平位置,为什么?
三、巩固提升
1.填空:
(1)等腰直角三角形的每一个锐角的度数是_____;
(2)(2018.成都)如果等腰三角形的底角等于40°,那么它的顶角的度数是_________ ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于____________ .
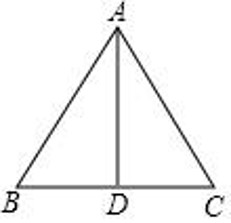
2.如图,有△ABC,已知AD是BC边上的中线。那么下列说法正确吗?为什么?
(1)AD也是△ABC的高线、角平分线;

(2)如果AB=BC,那么AD也是△ABC的高线、角平分线;
(3)如果AB=AC,那么∠A=∠B;
(4)如果AB=AC,且三角形的一个内角为50°,那么他的底角一定是65°;
(5)如果三角形是等边三角形,那么AD也是△ABC的高线、角平分线;
3.(2018.湘潭)如图,在等边三角形ABC中,点D是边BC的中点,则∠BAD=________.
4.如图,点P为等边△ABC的边BC上一点,且∠APD= 80°,AD=AP,求∠DPC的度数.
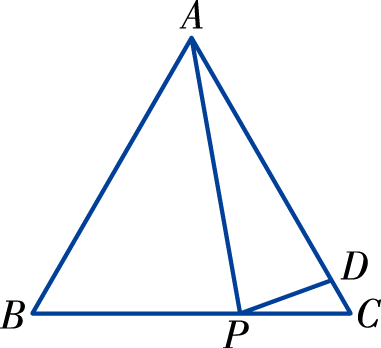
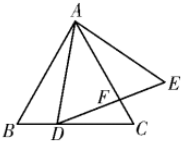
5.如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
四、课堂小结
这节课你学到了什么?
还有什么疑惑?
五、课后达标
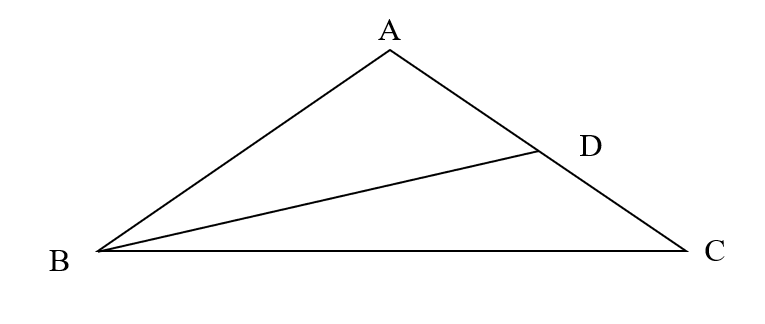
思考:如图,等腰三角形一腰上的中线把这个三角形的周长分为12cm和21cm两部分,则这个等腰三角形底边的长为?
设为正确答案