- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



三角形是最常见、最基础的几何图形之一,学生在前两个学段已学过三角形的一些知识,对三角形的许多性质有所了解,在第三学段的七年级有学过线段、角等知识,会简单的说理,这都为本节课的学习打下了坚实得到基础。再通过这节课深入了解三角形的概念,以及三角形的三边关系的探究与学习,为接下来三角形的其他概念的学习以及三角形的证明进一步打下基础,最后形成三角形这一知识点体系。学生正处在探索各类知识的学习阶段,将具体的事物总结成文字概念,学习三角形正好培养了学生能力。
圆规、三角板、PPT、电子教鞭、学生自备小棒
知识技能:在具体的情境中认识三角形,知道三角形的边,角,表示方法及三角形的分类;
数学思考:生活中的三角形在数学几何的应用,或生活中各种现象是否能用数学知识解释;
问题解决:探索出三角形的三边关系,解决一些生活中的实际问题;
情感目标:通过用三角形三边关系解决身边的问题,体会数学知识应用的价值,提高学生学习数学兴趣。
重点:三角形三边关系的探究和归纳
难点:三角形三边关系的应用
通过实际问题架设学习探索平台,教师采用点拨、引导的方法,启发学生经历主动思考。自主探索及合作交流的过程来达到对知识的“发现”和接受,进而完成知识内化,使书本知识成为自己的知识
一、认识三角形的相关概念
老师出示图片,并引导学生认识三角形的相关概念.
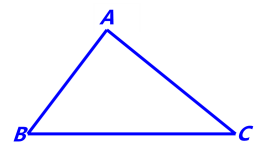
1、三角形用符号“△”来表示,即三角形ABC可记作△ABC
其中,点A,B,C 叫作△ABC的顶点;
∠A,∠B,∠C叫作△ABC的内角(简称△ABC的角);
线段AB,BC,CA叫作△ABC的边.
2、∠A的对边是BC,用小写字母a表示
∠B的对边是AC,用小写字母b表示
∠C的对边是AB,用小写字母c表示
3、BC边的对角是________,AC边的对角是________,AB边的对角是________.
答案:∠A,∠B,∠C
观察三角形的形过程,并听老师介绍三角形的顶点、角、边和表示方法。
二、三角形的分类
想一想 三角形应该怎么分类
1、三角形中有哪些几何元素?
2、哪些几何元素可以用来分类?
3、用角的角度来考虑,可以怎么分?
4、从边的角度来考虑,又可以怎么分?
从而得到三角形的分类:
按角分:锐角三角形
直角三角形
钝角三角形
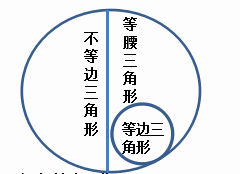
按边分:不等边三角形
等腰三角形:两边相等的等腰三角形
三边相等的等边三角形
等腰三角形 很高兴认识你
有两边相等的三角形是等腰三角形 如图:AB=AC
(师引导学生认识等腰三角形各部分名称)
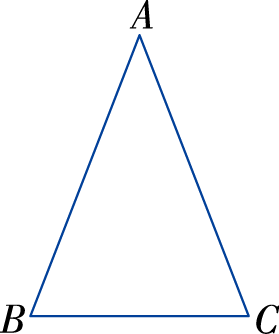
相等的两边叫作腰,另一边叫作底,两腰的夹角叫顶角,腰和底边的夹角叫作底角。
3、想一想:当等腰三角形的腰与底相等时,此时三角形为等边三角形,那么等腰三角形与等边三角形有何关系呢?
答案:等边三角形是腰和底边相等的等腰三角形.
等边三角形是特殊的等腰三角形
三、探究三角形三边间的关系
思考:如图,在A点的小狗,为了尽快吃到B点香喷喷的香肠,它会选择哪条路线?如果小狗在C点呢?
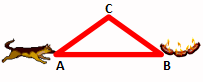
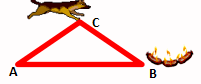
由“两点之间线段最短”基本事实得到:BC+AC>AB; AB+BC>AC; AB+AC>BC
得到三角形的三边关系:三角形的任意两边之和大于第三边
练习1:
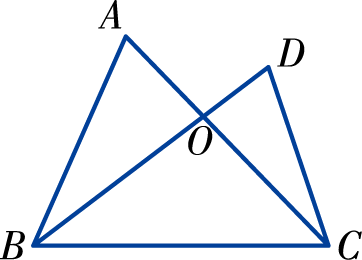
(1)如图,图中有几个三角形?把它们分别表示出来.
(2)如图,说出其中△BCD的三个内角.
(3)如图,写出∠D 的对边,BD 边的对角.
练习2
课堂抢答:1、三角形可分为等边三角形和等腰三角形.
2、等边三角形是特殊的等腰三角形.
3、等腰三角形至少两边相等.
4、等腰三角形的腰和底一定不相等
5、等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形
练习3 长度分别为6cm,4cm,3cm的三条线段能否组成三角形?
课堂巩固
1、一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是________.
2、四条线段的长分别为4cm,5cm,6cm,9cm任选其中三条线为边长构成三角形,选法有________种.
3、已知△ABC三边a、b、c、满足(a-b)2+|b-c|=0,则△ABC的形状是________.
4、已知△ABC三边为a、b、c、化简|a+b-c|+|b-a-c|.
设为正确答案