- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《找次品》是人教版数学五年级下册第8单元数学广角的内容。现实生活生产中的“次品”有许多种不同的情况,有的是外观与合格品不同,有的是所用材料不符合标准等。这节课的学习中要找的次品是外观与合格品完全相同,只是质量有所差异,且事先已经知道次品比合格品轻(或重),另外在所有待测物品中只有唯一的一个次品。
“找次品”的教学,旨在通过“找次品”渗透优化思想,让学生充分感受到数学与日常生活的密切联系。通过教学使学生受到数学思想方法的熏陶,形成探索数学问题的兴趣与欲望,逐步发展数学思维能力。
解决问题的策略研究学生已经不是第一次接触,此前学习过的“沏茶”、“田忌赛马”、“植树问题”“打电话”等都属于这一范畴,在这几节课的学习中,对简单的优化思想方法、通过画图的方式发现事物隐含的规律等都有所渗透,学生已经具有一定的逻辑推理能力和综合运用所学知识解决问题的能力.特别植树问题的研究思路在找次品的研究过程中很有借鉴作用,即化难为易,从简单的入手找到一般规律。
另外,本节课中会涉及到的“可能”、“一定”、等知识点学生在此之前都已学过的。
本节课学生的探究活动中要用到天平,在以往学习等式的性质等知识时,学生对天平的结构、用法以及平衡与不平衡所反映的信息都已经有了很好的掌握。
1.能够借助纸笔对“找次品”问题进行分析,归纳出解决这类问题的最优策略,经历由多样到优化的思维过程
2.通过观察、猜测、验证、推理等活动,使学生学会用天平找次品的方法,体会解决问题策略的多样性及运用“优化”的方法解决问题的有效性。
3.感受到数学在日常生活中的广泛应用,尝试用数学的方法来解决实际生活中的简单问题,初步培养学生的应用意识和解决实际问题的能力。
重点:
经历观察、猜测、试验、推理的思维过程,归纳出解决问题的最优策略。脱离实物,借助纸笔帮助分析“找次品”的问题。
难点:
脱离实物,借助纸笔帮助分析“找次品”的问题,发现并应用规律。



一、观看视频导入。

师:刚才的视频讲的是聪明的机器人找次品,今天我们也来学习找次品。
(2)今天我们我们就来学习用天平找次品。(板书课题:找次品)
二、探究新知。
1、认识天平。
师:今天老师遇到一个难题,想请同学们来帮忙?(出示题目)一起读题,题中要求我们用什么工具来找次品?
你见过没有砝码的天平吗?老师今天也带来了一个。(出示天平图)
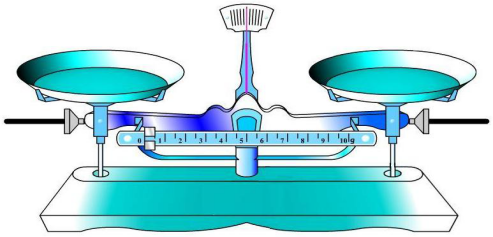
没有砝码的天平就像我们玩过的跷跷板一样,可以测出谁轻谁重。我们身上也有一架天平(伸开双臂,摇动双手,手掌向上,看这是天平的左盘,右盘)点击出示天平图2
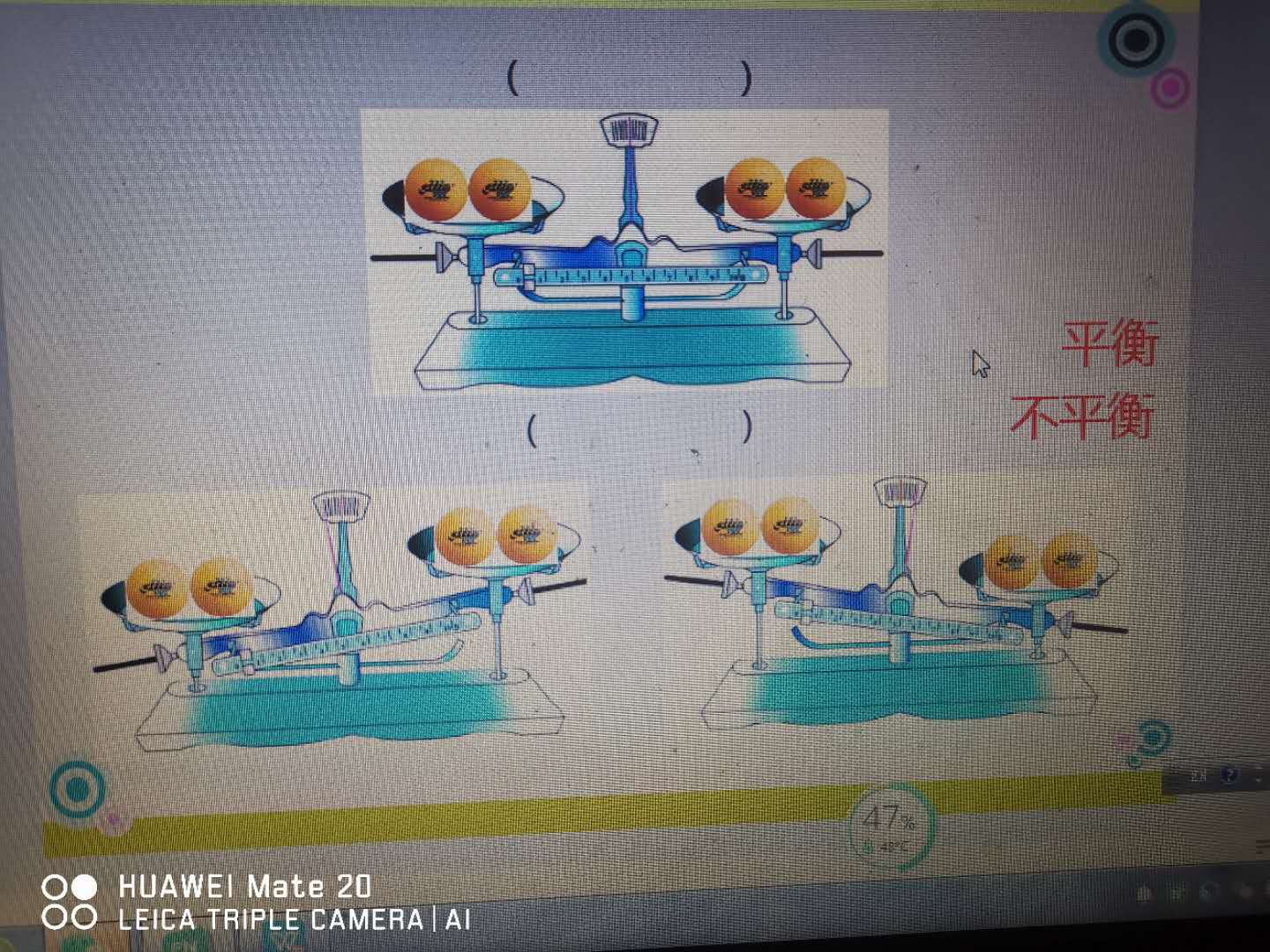
当天平两边放上物品是这幅图时,我们就说天平是平衡的,平衡说明左边和右边一样重。当天平是这两幅图时,我们就说天平是不平衡的。
当不平衡的时候,那个重球在哪儿啊?
师:接下来,题中还有哪些重要信息?(点击出示题目)

师:同学们太棒了.“至少称多少次,才能保证”是什么意思?)
生:肯定能找到次品的最少次数,不能靠运气。
二、以退为进,寻找策略
师:那究竟最少要多少次,才能保证把重球找出来呢?这个问题确实有点难,81个球太多了。你有什么好方法吗?
师:那老师这里有个好方法,化难为易。碰到难的事情,怎么办?从容易的开始研究,找到方法了,找到规律了,然后就可以解决那个难的问题。
1、研究2、3、4个球
师:你觉得,最简单是从几个球中去找?个
师:请问(出示2个球),两个球中只有一个重球,怎么用没有砝码的天平把它找出来?怎么分?怎么称法?
在这里,我在课件中用动画显示2个球的情况,当2个球放在平衡的天平上,天平一定是不平衡的。(达到多媒体技术与课堂教学的融合,再次直观演示。)
师:好!(出示3个球)请问,3个球中,只有一个重球怎么把它找出来?怎么分?怎么称法?借助一个学生身上的天平演示称法。
师:既考虑了平衡,又考虑了不平衡,思考得真全面!
师:(微笑)请看——(指板书,如下图)你有问题吗?你想提出个什么问题?
师:轻是相对于重而言,也就是说那个球是正常的球。为什么能推断出来?因为题目说了“只有一个稍重”。用没有砝码的天平来找重球,会有三种可能,有可能在第一个盘子,有可能在第二个盘子,还有可能在天平旁边。
师:继续来,接下来从4个球中找?怎么分?怎么称?
师:好!谁来说?
生1:平均分成2份,左盘2个,右盘2个,天平一定不平衡,接下来从下沉端2个中找,再天平左边1个右边1个,天平一定不平衡,下沉端为重球。称2次。
生2:分成3份,左盘1个,右盘1个,剩下2个放旁边。如果平衡,重球在旁边的两个球中,再分成1个在左盘,1个在右盘,天平一定不平衡,重球在下沉的一端。称2次。如果不平衡,重球在下沉的一端。称1次找到重球。
师:这样称,有1次,有2次的。那么,最少称几次,才能保证找到?
师:1次的,为什么不选?
生:那是运气好,不能保证。
师:这么看来,4个球中找出重球,可以有不同的方法,但最少要称2次。
2、研究8、9个球
师:接下来,多点吧,从8个球中找(有一个重球),怎么分?怎么称?
学生分组合作。
师:对!接着,请问,9个球中有一个重球,怎么找?独立思考后小组交流。
师:同样是9个球,一种称3次,一种称2次。请问,称2次是不是也是运气好的情况呢?
师:为什么不是运气最好的情况呢?
生:因为它是分成3个在一个盘子里的,不管平衡还是不平衡,接下来都是从3个里找,所以这是确保是2次的。
师:同意吧?掌声!也就是说,当我们不是把9分成(4,4,1),而是平均分成(3,3,3)的时候,而是不管平衡还是不平衡,都是2次能确保。
师:(指板书——8个球,3次;9个球,2次)有问题吗?这么多人能发现问题,你能提出什么好问题。
生:我觉得8个球中也能称2次保证找到次品。
师:提的好,你能说说具体称法吗?
生:先在天平的两边各放3个球,剩下的两个放旁边,如果平衡,重球就在旁边的两个中,接下来从2个中找;如果不平衡,重球就在下沉端的3个球中,接下来从中3个中找。都只需2次就确保找到次品。
师:现在,我们知道了8个球中找,最少2次就能称出来了。
师:孩子们,现在我们来分析,为什么同样是8个球,有的最少称3次,有的最少称2次?你发现这两个称法不同在哪?
生:一个分成2份,一个分成3份。
师:非常好的回答!看来,妙就妙在用上了第三个盘子。这第三个盘子是虚拟的。看到第三个盘子,高明;用上第三个盘子,就是高手。再看9个球时,为什么平均分就好些?是不是它充分地用上了第三个盘子,而不是把零头放在第三个盘子里。
师:通过上面的学习,你觉得找次品的最优方法是?
生:分成3份,尽可能平均分
师:课件展示找次品的最优策略。

三、巩固练习
抢答游戏
四、课后思考
学以致用,老师的难题,你们能解决了吗?从81个球中找一个稍重的球。
通过这节课的学习,你收获了什么?
设为正确答案