- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本章“锐角三角函数”属于三角学,从《数学课程标准》看,中学数学三角学内容分成两个部分,第一部分放在初中阶段,主要研究锐角三角函数和解直角三角形的内容。高中阶段的内容是三角学的主体部分,包括解斜三角形、三角函数、反三角函数和简单的三角方程。无论是从内容上看,还是从思考问题的方法上看,前一部分都是后一部分的重要基础,掌握锐角三角函数的概念和解直角三角形的方法是学习三角函数和解斜三角形的重要准备。
本章重点是锐角三角函数的概念和直角三角形的解法。锐角三角函数的概念既是本章的难点,也是学习本章的关键。难点在于锐角三角函数的概念反映了角度与数值之间对应的函数关系,这种角与数之间的对应关系,以及用含有几个字母的符号,
,
表示函数等,学生过去没有接触过,因此对学生来讲有一定的难度。至于关健,因为只有正确掌握了锐角三角函数的概念,才能真正理解直角三角形中边、角之间的关系,从而才能利用这些关系解直角三角形。
本章的难点是解直角三角形的应用,把实际问题转化为直角三角形中的问题,并通过锐角三角函数解决问题,该部分的难确点在计算上,要正确处理好数据间的关系,可借助计算器进行计算。
本节课的教学目标是:学生会利用相似三角形,探索并认识锐角三角函数()的定义;会根据已知直角三角形的边长求一个锐角的正弦值。
本章主要数学思想方法:
(1)数形结合,强调图形的作用
(2)方程思想在几何计算中的应用
1、九年级学生的思维活跃,接受能力较强,具备了一定的数学探究活动经历和应用数学的意识。
2、理解定义困难:锐角三角函数的定义是学生理解的难点,不能准确应用定义解决有关问题。
3、转化应用困难:在直角三角形中,学生习惯应用勾股定理解决问题,不会正确应用锐角三角函数的定义进行边的转化计算。
4、灵活应用困难:在解直角三角形的时候知道应用锐角三角函数,但是不能正确应用哪个锐角三角函数解题,从而造成运算麻烦,解题困难。
因此,在本节课的教学中,可让学生从已有的生活经验出发,参与知识的产生过程,在实践操作、自主探索、思考讨论、合作交流等数学活动中,理解和掌握数学知识和技能,形成数学思想和方法,让每个学生在数学上得到不同的发展,人人都获得良好的数学教育。
知识技能:
1、会利用相似直角三角形,探索并认识锐角三角函数()的定义.
2、会根据已知直角三角形的边长求一个锐角的正弦值.
过程与方法:
通过探索正弦的定义,培养学生观察、比较、分析、概括等逻辑思维能力.
情感、态度与价值观:
在自主探索、共同发现、共同交流的过程中分享成功的喜悦.
重点:理解并掌握正弦()定义,根据定义求锐角的正弦值.
难点:探索“在直角三角形中,任意锐角的对边与斜边的比值是一个常数”的过程.
4.1 正弦和余弦
概念:在中,
,锐角
的对边与斜边的比叫做
的正弦。记作
或
或
。
随
的增大而增大,
.
请同学们预习:课本P109—111,完成课前准备.
1、画一画:作一个,使得
,
2、量一量: ,
,
.
3、计算:,
.
问题:如图,一艘轮船从西向东航行到处,灯塔
在船的正北方向,轮船从
继续向正东方向航行到达
处,此时灯塔
在船的北偏西
方向,试问:从
处到灯塔
的距离
等于多少米?

(1)若,从
到灯塔
的距离
米?
(2)若,从
到灯塔
的距离
米?
归纳:直角三角形中,.
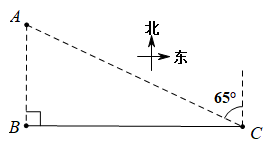
问题1:如图,一艘轮船从西向东航行到处,灯塔
在船的正北方向,轮船从
继续向正东方向航行
到达
处,此时灯塔
在船的北偏西
方向.
思考:(1)从处和灯塔
的距离
约等于 米?(精确到
)
(2)在直角三角形中,角的对边与斜边的比值是一个常数吗?
问题2:根据课前准备所作的直角三角形,可得,小组交流计算出的比值是否相等,由此你有何猜想?
几何画板展示:在中,
,
,拖动点
,改变
的大小,观察
的比值是否改变?
猜想:(1)在直角三角形中,角的对边与斜边的比值是一个常数。
(2)在直角三角形中,锐角的对边与斜边的比值是一个常数。
证明:如图,在中,如果
,
,那么
成立吗?
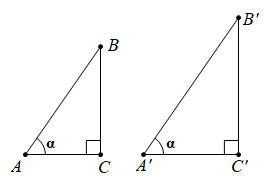
归纳:在一个锐角等于直角三角形中,角
的对边与斜边的比值是 ,与三角形的大小 .
定义:直角三角形中中,我们把的对边与斜边的比叫作
的正弦,记作
,即
.
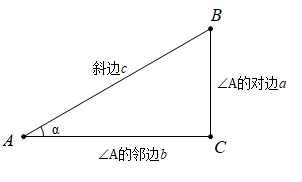
问题1:的正弦怎么表示?
问题2: .
问题3:当锐角增大时,这个锐角的正弦值如何变化?(小组交流讨论)
几何画板展示:如图在中,
,
,拖动点
,当锐角
增大时,
如何变化?
归纳:随
的增大而增大,
的范围是:
.
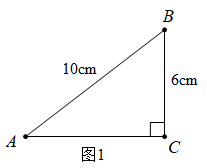
如图1:
1) ( )
2) ( )
3) ( )
4) ( )
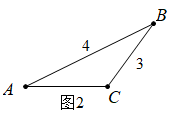
如图2:
5) ( )
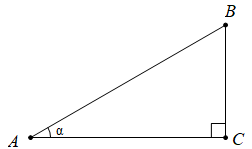
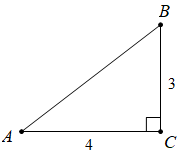
例1 如图,在中,
,求
和
的值.
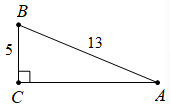
变式训练1:如图,在中,
,
,
,那么
,
.
变式训练2:如图,是平面直角坐标系上的一点,且
的坐标是
,则
__________。
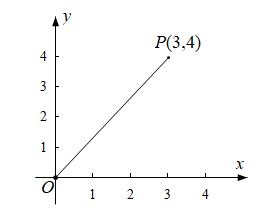
讨论:通过做题,你能发现什么结论?
归纳: .
例2 如图,在中,
,
,
, 求
和
的长。
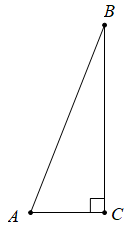
讨论:通过做题,你能发现什么结论?
归纳: .
如图,在中,
,
于点
。已知
,
。
(1)求的值。
(2)可以是哪两条线段之比?
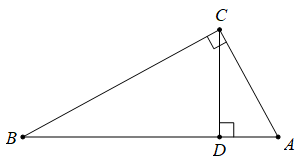
设为正确答案