- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



外接球问题在高考中多以选择题或填空题的形式呈现,难度中等或中等偏上,学生在这块内容如果掌握不好很容易丢分。有必要带动学生进行归纳总结外接球的模型,做到心中有数。
学生的立体几何已有一定的基础,但尚未形成系统化。
近些年的高考中,几何体的外接球几乎成了必考题,文科数学一般出现在11或12题的位置,理科数学一般出现在9或10题的位置,学生一般感觉比较难,没有相应的模型思想,部分学生根本无从下笔。
1.能将外接球问题归类总结;
2.熟练掌握外接球的基本公式以及四类常见模型及其处理方法;
1.可以补形变成长方体(或正方体)的外接球的模型
2.直棱柱(圆柱)、直棱锥的外接球模型
3.(正)棱锥(圆锥)的外接球模型
【外接球模型总结】
基本公式:
模型1: 长方体模型 :
正方体外接球半径:
模型2:可以补形变成长方体或正方体的模型,包括:
(1)墙角模型(三条线两两垂直);
(2)三组对棱分别相等的三棱锥(即四面体)模型;
(3)正四面体模型.
模型3:直棱柱(圆柱)、直棱锥模型(关键要素:有一条侧棱垂直底面)
(
为直棱(圆)柱或直棱锥的高,
为底面圆半径)
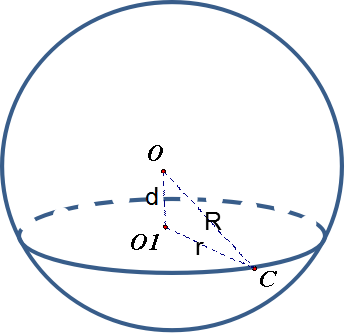
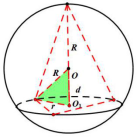
模型4:(正)棱锥、(圆锥)模型
(
为棱锥的高,
为底面圆半径)
任务一、外接球基本公式及长方体、正方体模型
【题型1】
1. 【2012课标文】(8)平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为 ( )
(A) 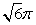 (B)
(B) 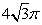 (C)
(C)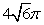 (D
(D
问题1. 题型1用到的公式是什么?
【题型2】
2. 【2017年Ⅱ卷文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为 .
3. 【2016年Ⅱ卷文4】体积为8的正方体的顶点都在同一球面上,则该球面的表面积为( )
A.12π B.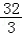 π C.8π D.4π
π C.8π D.4π
问题2. 你能对题型2归类出相应的外接球模型吗?结论是什么?
模型1.
探究一:与长方体相关的外接球模型
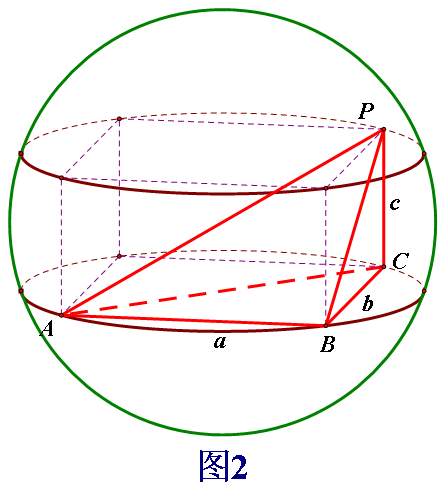
例1(1)已知三棱锥P﹣ABC的四个顶点均在球面上,PB⊥平面ABC.PB=2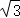 ,△ABC为直角三角形,AB⊥BC,且AB=1,BC=2.则球的表面积为( )
,△ABC为直角三角形,AB⊥BC,且AB=1,BC=2.则球的表面积为( )
A.5π B.10π C.17π D.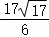 π
π
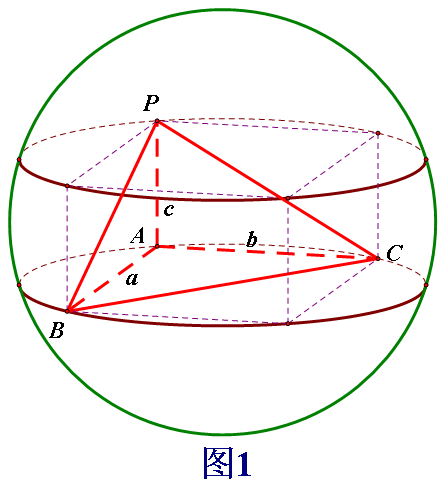
(2) 在三棱锥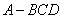 中,
中, 则三棱锥
则三棱锥 外接球的表面积为 __________.
外接球的表面积为 __________.
(3)棱长为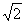 的正四面体的外接球的表面积为________.
的正四面体的外接球的表面积为________.
问题3. 你能对例1归类出相应的外接球模型吗?结论是什么?
模型2.
探究二:直棱柱(圆柱)、直棱锥模型(关键要素,有一条侧棱垂直底面)
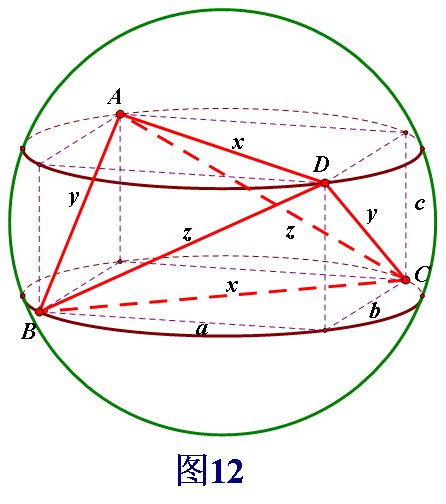
例2.(2009•全国卷Ⅰ)直三棱柱ABC﹣A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于 .

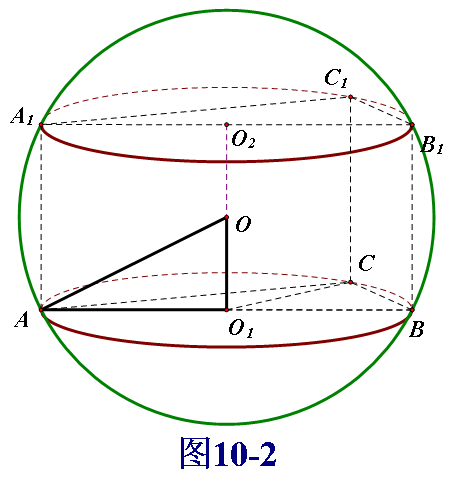
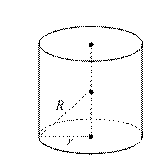
例2 变式.直三棱锥A1﹣ABC的各顶点都在同一球面上,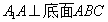 ,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于 .
,若AB=AC=AA1=2,∠BAC=120°,则此球的表面积等于 .
问题4. 你能归类出直棱柱(圆柱)、直棱锥相应的外接球模型吗?有什么样的结论呢?
模型3.
【当堂巩固练】直三棱锥A1﹣ABC的各顶点都在同一球面上,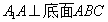 ,AA1=2,BC=2,∠BAC=60°,则此球的表面积等于 .
,AA1=2,BC=2,∠BAC=60°,则此球的表面积等于 .
探究三、棱锥(圆锥)模型
例3.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )
A. 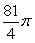 B.
B. 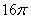 C.
C.  D.
D. 
问题5. 你能归类出锥体的外接球模型吗?有什么结论或方法?
模型4.
【当堂巩固练】正四面体的棱长为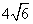 ,顶点都在同一球面上,则该球的表面积为 .
,顶点都在同一球面上,则该球的表面积为 .
【外接球模型总结】
基本公式
模型1: 长方体模型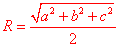 ,正方体外接球半径
,正方体外接球半径 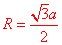
模型2:可以补形变成长方体或正方体的模型,包括:
①墙角模型(三条线两两垂直)
②三组对棱分别相等的三棱锥(即四面体)模型
③正四面体模型
模型3:直棱柱(圆柱)、直棱锥模型(关键要素,有一条侧棱垂直底面)
![]()
(h为棱柱的高,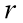 为底面圆半径)
为底面圆半径)
模型4:正棱锥的外接球![]()
课后巩固练习
1.【2011年理15改编】已知矩形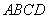 的顶点都在半径为4的球
的顶点都在半径为4的球 的球面上,且
的球面上,且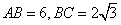 ,则球心到平面
,则球心到平面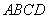 的距离为
的距离为
2. 已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为2,则该三棱锥的外接球的表面积是( )
A. 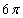 B.
B.  C.
C.  D.
D. 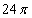
3.【2013年Ⅰ卷文15】已知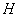 是球
是球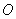 的直径
的直径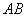 上一点,
上一点,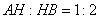 ,
,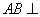 平面
平面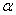 ,
,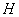 为垂足,
为垂足, 截球
截球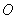 所得截面的面积为
所得截面的面积为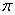 ,则球
,则球 的表面积为_______.
的表面积为_______.
4.(2014•陕西)已知底面边长为1,侧棱长为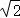 的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
A. 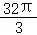 B.4π C.2π D.
B.4π C.2π D.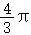
5.【2017年Ⅲ卷文9】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.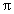 B.
B. C.
C.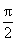 D.
D.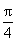
6.【2008年文15】一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为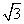 ,底面周长为3,那么这个球的体积为 _________
,底面周长为3,那么这个球的体积为 _________
7.已知矩形ABCD,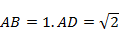 ,E为AD的中点,现分别沿BE,CE将
,E为AD的中点,现分别沿BE,CE将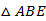 ,
,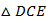 翻折,使点A,D重合,记为点P,则几何体
翻折,使点A,D重合,记为点P,则几何体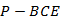 的外接球表面积为( )
的外接球表面积为( )
A. 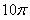 B.
B.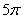 C.
C.  D.
D. 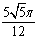
8.(2018全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点, 为等边三角形且其面积为
为等边三角形且其面积为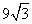 ,则三棱锥
,则三棱锥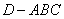 体积的最大值为( )
体积的最大值为( )
A.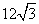 B.
B.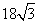 C.
C.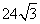 D.
D.
9.(2007•全国卷Ⅰ)正四棱锥S﹣ABCD的底面边长和各侧棱长都为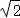 ,点S、A、B、C、D都在同一个球面上,则该球的体积为 .
,点S、A、B、C、D都在同一个球面上,则该球的体积为 .
设为正确答案