- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《认识不等式》是华东师大版《义务教科书·数学》七年级下册第八章第一节,不等式从某种程度上讲是等式的延伸,它是理解函数相关问题的重要基础,今后高等数学中涉及到的优化问题都与之有所关联,不等式还是刻画现实世界中数量关系的数学模型,贯穿于整个初中数学学习的始终,起到承上启下的作用。
学生在小学对数量大小的比较和不等量关系有了一定的理解,但对含未知数的不等式还是陌生的。从数到式,从方程到不等式的转换需要一个过程,对不等式的解也需要在探索的过程中慢慢体会。学生列不等式时,对数量关系中的“不小于”、“不大于”、“非负数”等数学术语的含义理解容易产生混乱,建立不等式关系的能力有待提高。
1、能从现实活动中抽象出不等式,理解不等式的概念,能正确地判断所给的式子是否是不等式;
2、正确理解“不大于”、“不小于”、“非负数”等数学术语的含义,能列出正确的不等式;
3、理解不等式的解的意义,能写出所给不等式的几个解,并会检验一个数是否是一个不等式的解。
4、经历由具体实例建立不等式模型的过程,经历从特殊到一般的探究过程,并进一步发展学生的符号感和数学化的能力。
重点:理解不等式及不等式的解的意义,会用不等式正确表达量之间的关系。
难点:不等式解的概念,不等号“≥”和“≤”地准确运用

一、情境导入
1.请学生数一数教室里正在上课的男、女同学各有多少人,引出不等号以及不等关系。
假设在人数较少的一边不断加人,从不等到等,再到不等,逐步引入未知数x。
2、请学生说一说:日常生活中还有哪些不等关系?
学生畅所欲言,感受不等关系无处不在……
思考:对于不等关系问题,如何用式子来表示?
3.板书课题:8.1认识不等式
二、探索新知
(一)不等式的概念
1.提问:不等符号只有“>”和“<”吗?你还知道哪些常用的不等号?
2.出示交通指示牌“限载25t”“限速50”,思考:你是如何理解的?
学生分组讨论,由小组代表说一说讨论结果。
师生共同小结:“不超过、不大于、至多”可用“≤”表示,“不低于、不小于、至少”可用“≥”表示。
补充:表示不相等的关系,都可以用一个符号来表示——“≠”。
3.引导学生回忆等式的概念(用等号表示相等关系的式子叫做等式),类比得出不等式的概念:用不等号表示大小关系的式子,叫做不等式。
4.速度挑战:全班参与,在规定时间内找出不等式,看谁速度快,让学生自然而然总结出“判断所给式子是否是不等式的方法”——看是否含不等号。
5.(再次巩固)PK小游戏——找出不等式:
从男、女同学中各找一位代表上台pk,检测学习效果。
6.播放视频——《不等式的发展史》,渗透数学文化,激发学生学习数学的兴趣。
(二)不等式的解的概念
1.出示问题情境:世纪公园的票价5元/张;一次购票满30张,每张可少收1元。
2.学生根据理解填写:
(1)如果x<30,按实际人数买票应付款________元;
(2)如果x≥30,按实际人数买票应付款________元。
3.思考:某天,七年级(1)班有27名同学组织去世纪公园游玩,如果你是领队,你会怎样买票?
学生分小组讨论,教师帮助小结得出结论:27人买30张票合算。
4.引导学生进一步思考:
(1)是不是少于30人都选择买30张票呢?
(2)少于30人时,究竟多少人买30张票反而合算呢?
(分析:当x<30时,按实际人数要买x张,付款5x(元),买30张票要付款4×30=120元,如果买30张票合算,那么应有120<5x)
借助表格探究,学生分小组合作完成:
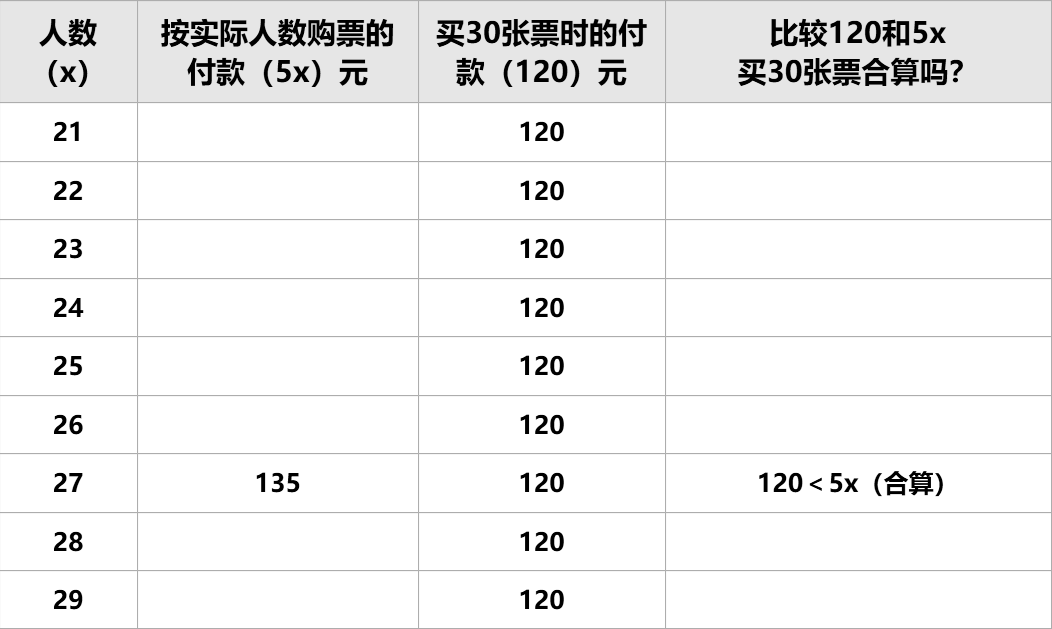
学生根据表格讨论:
(1)当x=_____时,两种付款方式花的钱一样多,_________成立;
(2)当x=____________________时,买30张票合算,__________成立。
学生回忆方程的解的概念(能使方程左右两边相等的未知数的值,叫做方程的解),类比得出不等式的解的概念:能使这个不等式成立的未知数的值,叫做不等式的解。
5.剥离问题情境,想想不等式120<5x还有没有其他解?
三、应用新知
【例1】下列数中:
0,﹣3,3,4,﹣0.5,﹣20,﹣0.4
____是方程x+3=0的解;___________________是不等式x+3>0的解。
(引导学生通过检验一个数是否是方程的解的方法,得出检验一个数是否是不等式的解的方法:将数值代入不等式,看是否成立。)
【练习1】x=-1不是下列哪个不等式的解( )
A.2x+1≤-3 B.2x-1≥-3 C.-2x+1≥3 D.-2x-1≤3
【例2】用不等式表示下列关系,并写出两个不等式的解:
(1)x的一半小于-1;
(2)y与4的和不大于0.5;
(3)a是负数;
(4)b是非负数。
归纳列不等式的基本步骤:
(1)抓关键词,找出不等关系,选择合适的不等号来表示;
(2)根据题意,列代数式表示不等关系两边的量。
【练习2】
(1)“x的相反数与3的和是正数”,用不等式可表示为_____________;
(2)请说出不等式“3y-2x<0”表示的含义_____________________.
【实际应用】
丁丁和当当每月都有零花钱,他俩约定存钱,在母亲节给自己的妈妈买礼物。这个月丁丁存了50元,当当存了35元。从下个月开始,丁丁每月存15元,当当每月存20元。几个月后当当的存款数能超过丁丁?(根据题意列出不等式)
四、课堂小结
这节课你学到了什么?分享一下你有哪些收获?
五、作业布置
1.导学案《课后作业》
2.预习下节课的学习内容
设为正确答案