- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
一元二次方程根与系数的关系在初中阶段属于选学内容，但在高中阶段的学习中有着广泛的应用。因此，在学习了公式法后，有必要与学生共同讨论一元二次方程根与系数之间的其他关系。引导学生归纳猜测一些数学中的规律。培养学生的归纳思维。所以本节课也算是公式法的延续。通过这节课是初中阶段知识的延续拓展，通过本节课的学习既对初中阶段的知识进行了拓展延伸又为高中知识进行了储备。
九年级的学生已学习用求根公式法解一元二次方程，对于公式式求一元二次方程的根掌握的比较熟练。
经历从特殊到一般也能够推导出一元二次方程两根之和与两根之积与方程的系数的关系。
通过一般的推导，让学生更好的得出根与系数的关系。扩大学生的探索空间，增强学生的探索欲望。
知识与技能：了解一元二次方程的根与系数的关系；不解方程求与一元二次方程的根有关的代数式的值。
过程与方法：引导学生在已有的一元二次方程解法的基础上，探索一元二次方程根与系数的关系与应用。
情感、态度与价值观：经历从特殊到一般的探究过程，培养学生自主归纳探究能力、推理论证能力、合作交流的能力。
教学重点：一元二次方程根与系数的关系及简单运用。
教学难点：一元二次方程根与系数的推导。
一元二次方程根与系数的关系
一知识探究
方 程 | x1 | x2 | x1+x2 | x1x2 |
x2+2x=0 | ||||
x2+3x-4 =0 | ||||
2x2-3x+1 =0 |
二：动脑筋
当Δ≥0时，设ax2＋bx＋c＝0(a≠0)的两个根为x1，x2，则x1＋x2＝________，x1x2＝________．
三：典型例题分析：
例1 不解方程，求下列方程的两根之和与两根之积：
(1)x2－6x－15＝0； (2)3x2＋7x－9＝0；
(3)5x－1＝4x2.
例2 已知方程2x2＋kx－9＝0的一个根是－3，求另一根及k的值．
跟踪训练
1．两根均为负数的一元二次方程是( )
A．7x2－12x＋5＝0 B．6x2－13x－5＝0
C．4x2＋21x＋5＝0 D．x2＋15x－8＝0
2．已知x1、x2是方程x2－3x－2＝0的两个实根，则(x1－2)（x2－2)＝________.
3．利用根与系数的关系，求下列方程的两根和与两根积：
(1)x2－3x＝15； (2)5x2－1＝4x2；
(3)x2－3x＋2＝10; (4)4x2－144＝0；
4．已知x1，x2是方程x2－4x＋2＝0的两根，求代数式x1＋x2的值．
5.归纳小结：
6.作业
出示教学目标。
1．理解并掌握根与系数关系：x1＋x2＝
，x1x2＝
2．会用根的判别式及根与系数的关系解题．
（一）知识回顾：
1：一元二次方程的一般形式是 。
2. 一元二次方程根的判别式是 。
3. 当∆≥0时，方程可以用求根公式写出它根，一元二次方程的求根公式是 （二）探究新知：
1.填表，观察，猜想。
方程 | x1,x2 | x1+x2 |
| x1x2 |  |
x2-2x+1=0 | |||||
x2+3x-10=0 | |||||
2x2-3x+1=0 |
（二）猜想结论:
(1)问题：你发现什么规律？
①用语言叙述你发现的规律:
.
② 一元二次方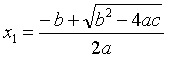
程ax2+bx+c=0 (a 
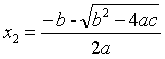0)的两根x1，x2， 请用式子表示你发现的规律.
（三）论证结论：
一元二次方程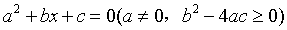
的两个根为 x1，x2 。
，
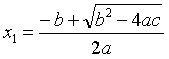x1+x2 = x1x2=
（四）归纳结论：
一元二次方程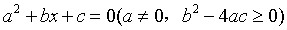
的两个根为 x1，x2 。
则：x1+x2 = x1x2 =
（五）例题讲解：
例1： 根据一元二次方程根与系数的关系，求下列方程的两根x1，x2的和与积：
（1） 2x2－3x＋1 = 0 ；
（2） x2－3x＋2 = 10 ；
（3） 7x2－5 = x＋8 .
例2 已知方程５x²+kx-6=0的一个根是２，求它的另一根及 k 的值．
（六）巩固练习：
1.根据一元二次方程根与系数的关系，求下列方程的两根的和与积：
（1）x2-6x+1=0； （2）2x2-x=6 .
2. 已知方程 5x2-7x+k=0 的一个根是2, 求它的另一个根及 k 的值.
（七）拓展提升
1.已知x1，x2是方程x2＋6x＋3＝0的两实数根，试求下列代数式的值：
(1)x1＋x2；
(2)x1＋x2；
(3)(x1＋1)(x2＋1)．
（八） 课堂小结
学生试述：今天学到了什么？
设为正确答案
