- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



“平行四边形的性质”是全章的重点之一,它是在学生已掌握了平行线的性质、全等三角形和四边形的有关知识的基础上研究的,既是已学知识的综合运用,也是下一步研究各种平行四边形的性质和判定的基础,具有承上启下的重要作用。同时这些知识在日常生活中经常会用到,具有很强的实用性。通过本节课的学习还可以向学生渗透“转化”的思想,提高学生分析问题和解决问题的能力。
学生在小学阶段就已经对平行四边形有了初步、直观的认知,能够指出哪样的图形是平行四边形,并且知道平行四边行的对边分别平行,为平行四边形性质的研究提供了一定的认知基础。而这节课的教学目的是让学生掌握平行四边形对边相等、对角相等的性质。八年级学生的严密的推理论证能力有所欠缺,从实际生活中的平行四边行入手,能让学生更容易理解和接受。
1.理解平行四边形的概念;
2.掌握平行四边形边、角的性质;
3.利用平行四边形边、角的性质解决问题.
1.理解平行四边形的概念;(重点)
2.掌握平行四边形边、角的性质;(重点)
3.利用平行四边形边、角的性质解决问题.(难点)
2.2.1平行四边形的性质
1.平行四边形的定义
2.平行四边形的边、角的性质:对边相等,对角也相等。
在小学, 我们已经认识了平行四边形. 在图2-10 中找出平行四边形,并把它们勾画出来.


生活中,你还在哪见过平行四边形呢?怎样的四边形是平行四边形?
1、定义:
准备几个多边形的道具,让学生找出其中的平行四边形,并通过这个活动说一说什么样的多边形叫做平行四边形。
引导并让学生回答:两组对边分别平行的四边形 叫做平行四边形。
平行四边形有怎样的性质呢?
通过观看一段微课视频,回答平行四边形有怎样的性质?
(教师在黑板上画上平行四边形)
让学生继续观察平行四边形教具,同时使用尺子及量角器等工具找一找平行四边形边和角的特点。
分小组讨论:证明平行四边形的对边相等、对角相等(简要说明证明思路)
小组讨论,教师注意引导
多找几名学生回答,并让一位学生总结。
在图2-13的□ABCD中,连接AC.
∵ 四边形ABCD为平行四边形,
∴ AB∥DC ,BC∥AD(平行四边形的两组对边分别平行).
∴ ∠1=∠2 , ∠4=∠3.
又 AC =CA,
∴ △ABC≌△CDA.
∴ AB = CD,BC = DA,∠B =∠D.
又∠1+∠4=∠2+∠ 3.
即∠BAD=∠DCB.
同学们共同说出结论:平行四边形对边相等,平行四边形的对角相等.
口算回答1.在平行四边形ABCD 中,AD=40,CD=30,
∠B=60º;,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
2.在平行四边形ABCD 中,∠D=120º;, ∠CAD=20º;,则∠B= , ∠CAB=
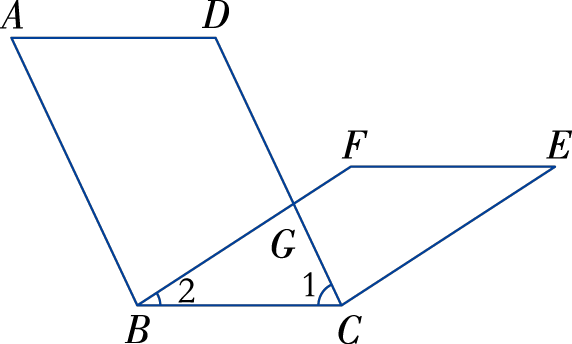
例2 如图2-14,四边形ABCD和BCEF均为平行四边形,
AD =2cm,∠A =65°,∠E =33°,求EF 和∠BGC.
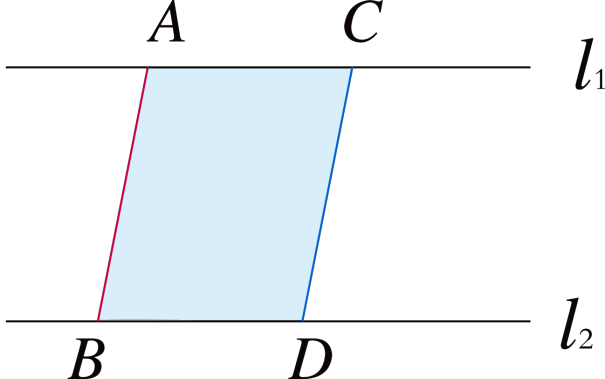
例1如图2-15,直线l1与l2平行,AB,CD是l1与l2之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
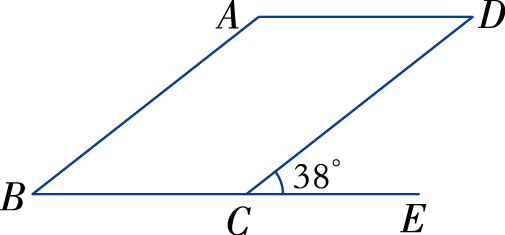
1. 小试牛刀
如图,□ABCD的一个外角为38º;,求∠A,
∠B,∠BCD,∠D的度数.
2、粮食储备
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?

3.探险时刻
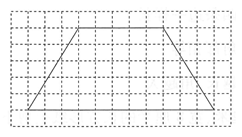
(1)在下面的图形中分别画一条满足要求的线。1、分成一个平行四边形和一个三角形。
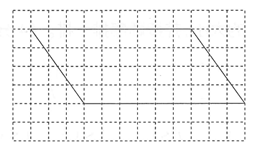
(2)分成两个平行四边形。
本堂课你学到了什么?
学生小结:了解并接触了平行四边形;知道了它在生活中的应用,是生活中的常见图形;学习并掌握了平行四边形对边相等,对角也相等的性质。
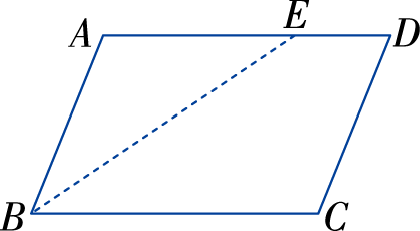
如图,在□ABCD中,∠ABC= 68°,BE平分 ∠ABC,交AD于点E. AB=2cm,ED=1cm.
(1)求∠A,∠C,∠D的度数;
(2)求□ABCD的周长.
解:(1)答: ∠A =112°;
∠C= 112°;
∠D = 68° .
(2) 由已知可得∠ABE=∠AEB.
∴ AE = AB =2cm,
∴ AD= AE+ED=2+1=3 (cm).
∴ □ABCD的周长=2 (AD+ AB)=2×(3+2)=10 (cm).
学法大视野《平行四边形的性质》
利用平行四边形设计美丽图案,表达你的美好愿望。
设为正确答案