- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《幂函数》选自高一数学新教材第一册第3章《函数的概念与性质》第3节,教科书将幂函数的内容安排在函数的一般概念和性质之后,是学生进入高中后学习的第一类具体的基本初等函数. 幂函数的教学在基本初等函数的教学中起着“铺垫”、“模板”的作用,幂函数的学习有着“承上启下”的作用,既是对前面函数的概念与性质的总结,又将这些方面系统的应用到一类具体的函数——幂函数上面,为后面指数函数、对数函数、三角函数的学习提前提供了思路和模板。因此,《幂函数》这堂课的教学和学习至关重要。
学生在初中已经研究过正比例函数、二次函数、反比例函数,等,这些函数学生都非常熟悉. 这节内容是对初中有关内容的进一步概括、归纳、发展,是与幂有关知识的高度的升华,导学案和PPT的设计至关重要,我们在知识的安排方面要环环紧扣,做到过度自然、思维紧凑,要体现知识的发生、发展过程。通过《幂函数》这堂课的学习,学生需体会研究一类函数的“基本套路”,形成系统的学习函数的基本方法。幂函数的学习对学生来说无论是获取知识还是获取知识的研究方法,都是极为重要的。因此,本节内容的学习可以看成是一般函数概念与性质的下位学习。
学生通过这节课内容的学习,可以系统的去了解研究一类函数,主要从以下几个方面思考:函数的三要素,定义域、值域、解析式、以及通过画函数的图像去研究函数的单调性及奇偶性等。这个过程体现了数学课程教学的统筹思想,体现了教学中的组织化,系统化的精神。特别需要强调的是,学生需要通过这节课去体会函数学习、探究的方法,需要学生去动手操作,合作探究,实现知识的内化,让学生在脑海中形成深刻的印象,以便能更好的将该方法迁移到对其他函数的研究.
学生在初中已经学习过一些具体的幂函数,但缺乏对研究一类函数的内容和方法的认识,教学时应联系初中学习函数的经验,以及前面学习过的一般函数的概念和性质,让学生尝试构建本节课的学习思路,从而体会研究一类函数的内容、思路和方法.
(1)在第三章的学习中,学生已经接触过函数的定义域、对应关系及其值域。并确立了利用函数的定义域、解析式、值域、通过画函数的图像研究单调性、奇偶性等去研究一个函数的意识,已初步形成对数学问题的合作探究能力。
(2)虽然在初中阶段的学习中,学生已经接触过这几种幂函数,并且学生也学会用用描点法绘制函数的图像,但是对于幂函数
的图象画法仍然不够熟练,容易出错,并且在这节课的研究内容中,学生对这两个函数还不熟悉,自然这个环节的重点就在于告诉学生如何画这两个函数的图象,取特殊点
区别哪个函数图像在最下方,逐个分析每个图像的位置。
(3)大部分学生的画图能力还有待提高,适当多给一些作图时间。
(4)在通过图像研究一般幂函数时,学生以小组合作探究的形式进行,学习已经有小组讨论的经验,但是我们需要多给每个小组的讨论和发言时间,各小组相互补充,最后教师汇总点评,实现教师引导,学生自主观察,发现,归纳,整堂课的知识生成都来源于学生。
知识与技能:(1)理解幂函数的概念,学会以简单的幂函数为例研究函数性质的方法。
(2)理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题。
过程与方法:通过师生一起合作探究、学生小组探究的方式,培养学生数形结合的思想,培养学生对知识概括的能力,培养学生由特殊到一般的思想。
核心素养:借助幂函数的性质及简单应用,提升逻辑推理、数学抽象与数学运算素养。
教学重点:理解幂函数的概念,学会以简单的幂函数为例研究函数的性质方法。理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题。
教学难点:理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题。
幂函数 1、幂函数:一般地, 注意:只有一项且前面系数为1. 2、幂函数的性质: 1、幂函数的性质 (1) 过定点(1,1),且图像不过第四象限; (2) 为 (3)当 当 (4)画直线 |
PPT展示区 |
例3. 教师示范区 |
| 学生板题、草稿区 |
问题1:(1)如果张红购买了每千克1元的蔬菜x千克,那么她需要付的钱数y(元)和购买的蔬菜量x(千克)之间有何关系?
(2)如果正方形的边长为x,那么正方形面积y=_____?
(3)如果正方体的棱长为x,那么正方体体积y=_______?
(4)如果正方形场地的面积为x,那么正方形的边长y=_______?
(5)如果某人x秒内骑车行进1千米,那么他骑车的平均速度y= _________?(千米/秒)
问题2:写出上述问题中的函数并仔细观察,以上函数解析式有什么共同特征?
问题2:函数有哪些共同特征?
答案参考:(1)都是以自变量x为底数;
(2)指数为常数;
(3)自变量x前的系数为1;
(4)只有一项。
师引导:像具有以上四个特征的函数就是我们今天所学的幂函数(引出课题),如何定义幂函数呢?
答案参考: 一般地,函数叫做幂函数,其中是
自变量,
是常数.
练一练1:判断以下函数是否为幂函数,找一个同学口答(对概念的进一步理解、巩固)
(1)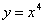 ; (2)
; (2)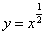 ; (3)
; (3)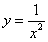 ; (4)
; (4)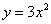 ;
;
(5) 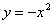 ; (6)
; (6)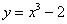 .
.
练一练2:已知幂函数的图象过点
,则
__________
练一练3:已知是幂函数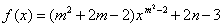 ,则
,则
分析:只有一项,这项的系数为1
设计意图:进一步理解并应用幂函数的概念
思考1:结合以往学习函数的经验,你认为应该从哪些方面去研究这五个常见的幂函数?
函数的三要素、图像、单调性、奇偶性
设计意图:回顾所学过的函数的几个方面,同时给出研究函数的统一模板
探究活动:以小组为单位画图并探究幂函数的性质!
探究1:逐个画出五个幂函数的图像并分析其性质
![]()
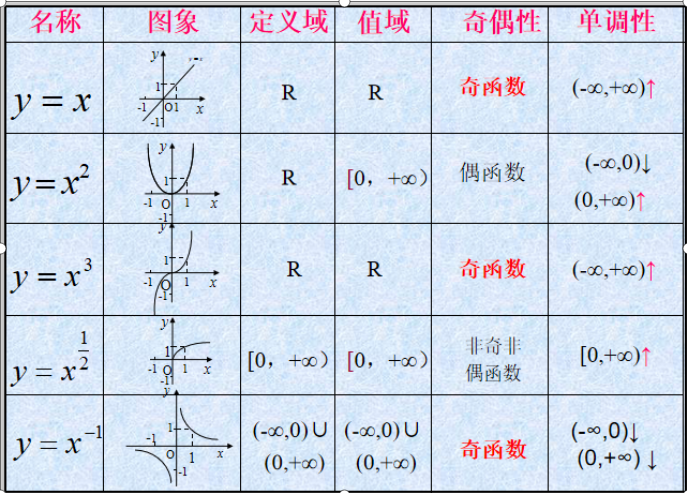
探究2:
在同一平面直角坐标系内作出幂函数y=x,y=x2,y=x-1,y=x3,y=x1/2的图象.(用几何画板画图)
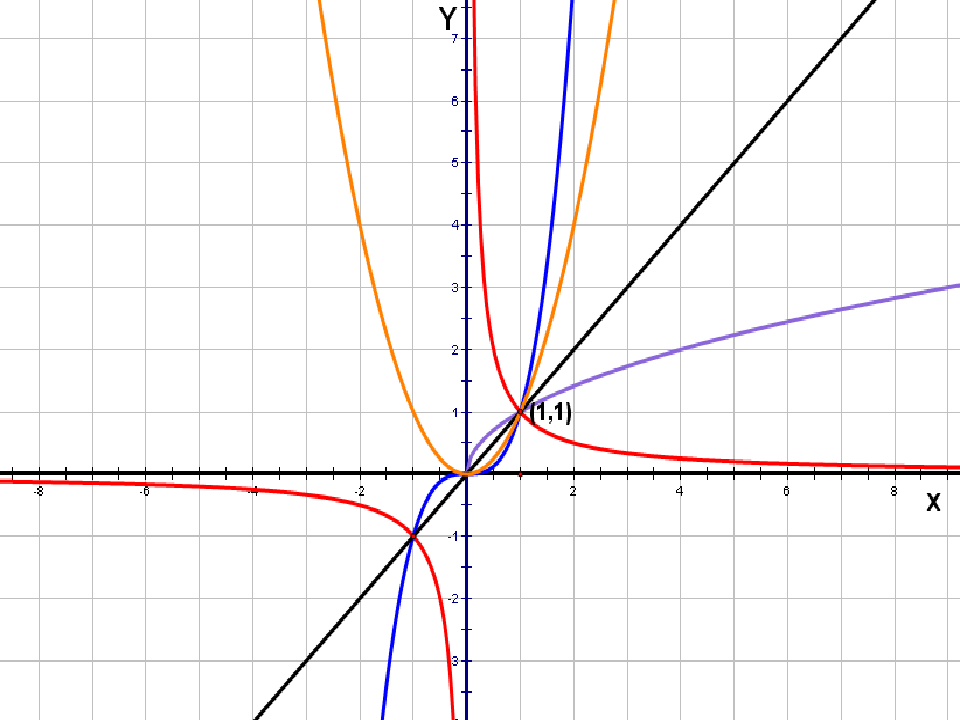
思考2:仔细观察,你能得到这五个幂函数图像的共同特征吗?
思考3:这五个幂函数中,哪些是奇函数,哪些是偶函数?
思考4:这五个幂函数在(0,+∞)上中哪些是单调递增哪些是单调递减?
思考5:幂函数在(0,+∞)上的单调性如何?
思考6:在第一象限画一条直线与幂函数
的图像相交,交点的位置与指数有什么关系?
幂函数的性质
(1) 过定点(1,1),且图像不过第四象限;
(2) 为奇数时,
为奇函数;
为偶数时,
为偶函数;
(3)当时,
在(0.+
)上为增函数;
当时,
在(0.+
)上为减函数;
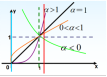
(4)画直线,图上指大!
例1.如图是幂函数和在第一象限内的图像,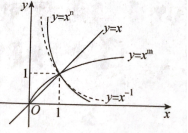
则( )
A. B.
C. D.
设计意图:考察“图上指大”
例2. 比较大小.
(1) (2)
(3) (4)
设计意图:通过(1)示范构建新函数,利用函数单调性比较大小的方法;通过(4),讲两种解法,注意分数指数幂的化简,幂函数单调性质的应用
例3. 若,求
的取值范围.
设计意图:进一步利用幂函数的单调性解决含参类问题,注意考虑定义域
1、 幂函数的定义,幂函数的性质;利用幂函数的单调性判别大小
2、幂函数的学习过程中的数学学习思想和方法:(1)研究一类函数研究它的定义域、解析式、值域、图像、单调性、奇偶性的等几个方面;(2)数形结合和从具体到一般的转化思想(通过几个具体的幂函数得到一般幂函数的概念,通过五个具体的幂函数的性质总结一般幂函数的性质)
设为正确答案