- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



“将军饮马”问题是湘教版八年级数学上册第二章的选写内容,是在学生已经学习过轴对称、全等三角形的基础上,再利用两点之间线段最短这一基本事实综合探究这一问题。它既是轴对称、三角形知识运用的延续,又能培养学生学会思考,自主探究的能力.在知识与能力转化上起到桥梁作用.本节课的学习过程体现了建模、类比、化折为直转化的数学思想方法。
将军饮马问题从本质上说是最值问题,作为初中生,在此之前很少涉及最值问题,解决这部分问题的经验尚浅,特别是面对有具体背景下的最值问题,更会感到陌生,无从下手.授课班级是普通初中实验班,学生基础较好,有一定的探究能力,合作素质较好,对前面轴对称,全等三角形等知识有一定储备,但学生很难将这个模型从复杂的图形中抽离出来,只有明白其中原理,掌握模型的特征,才能以不变应万变。
知识与技能目标:
1. 能利用轴对称解决简单的最短路径问题,体会图形的变化在解决最值问题中的作用,感悟转化思想;
2. 能做出一个图形经轴对称变化后的图形;
3. 能利用轴对称变换解决日常生活中的实际问题.
过程与方法目标:
1. 运用基本作图,能解决实际问题中的最短路径问题;
2. 通过对基本几何模型的探究,从异侧到同侧,体会转化思想在数学问题中的妙用.
情感态度与价值观目标:
1. 进一步培养学生的作图意识和作图情感,并根据实际问题进行简单的作图;
2. 让学生明确作图的应用思想,体会作图在实际生活中的用处;
3. 进一步培养学生的动手习惯和作图能力,提高学生的数学应用性思维;
4. 让学生体会到数学来源于生活,高于生活又服务于生活,激发学生对数学的学习兴趣.
教学重点是:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题,培养学生解决实际问题的能力;
教学难点是:如何利用轴对称将最短路径问题转化为线段和最小问题.
最短路径问题——以将军饮马为例
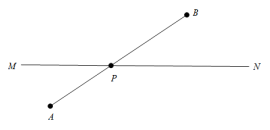
异侧问题 现学现用 1
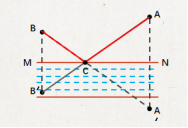
同侧问题 学生上台板书
验证:AP'+P'B>AP+PB 演示学生的练习实战演练2
因为AP+PB=A'B 又AP'+P'B>A'B
即有AP'+P'B>AP+PB
所以AP'+P'B>A'B
“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”.
【问题描述】
传说亚历山大城有一位精通数学和物理的学者,名叫海伦.
一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
将军每天骑马从城堡出发,到军营,途中马要到小溪边饮水一次.
将军问:怎样走路程最短?

这就是被称为"将军饮马"而广为流传的问题.
设计意图:通过实际生活中经典的一个数学问题让学生产生学习的兴趣,并让学生在探究过程中体会,如何学以致用
例1.如图:一位将军骑马从城堡A到城堡B,途中马要到河边饮水一次,问:这位将军怎样走路程最短?

几何画板展示:存在一点P使得将军走的路程最短
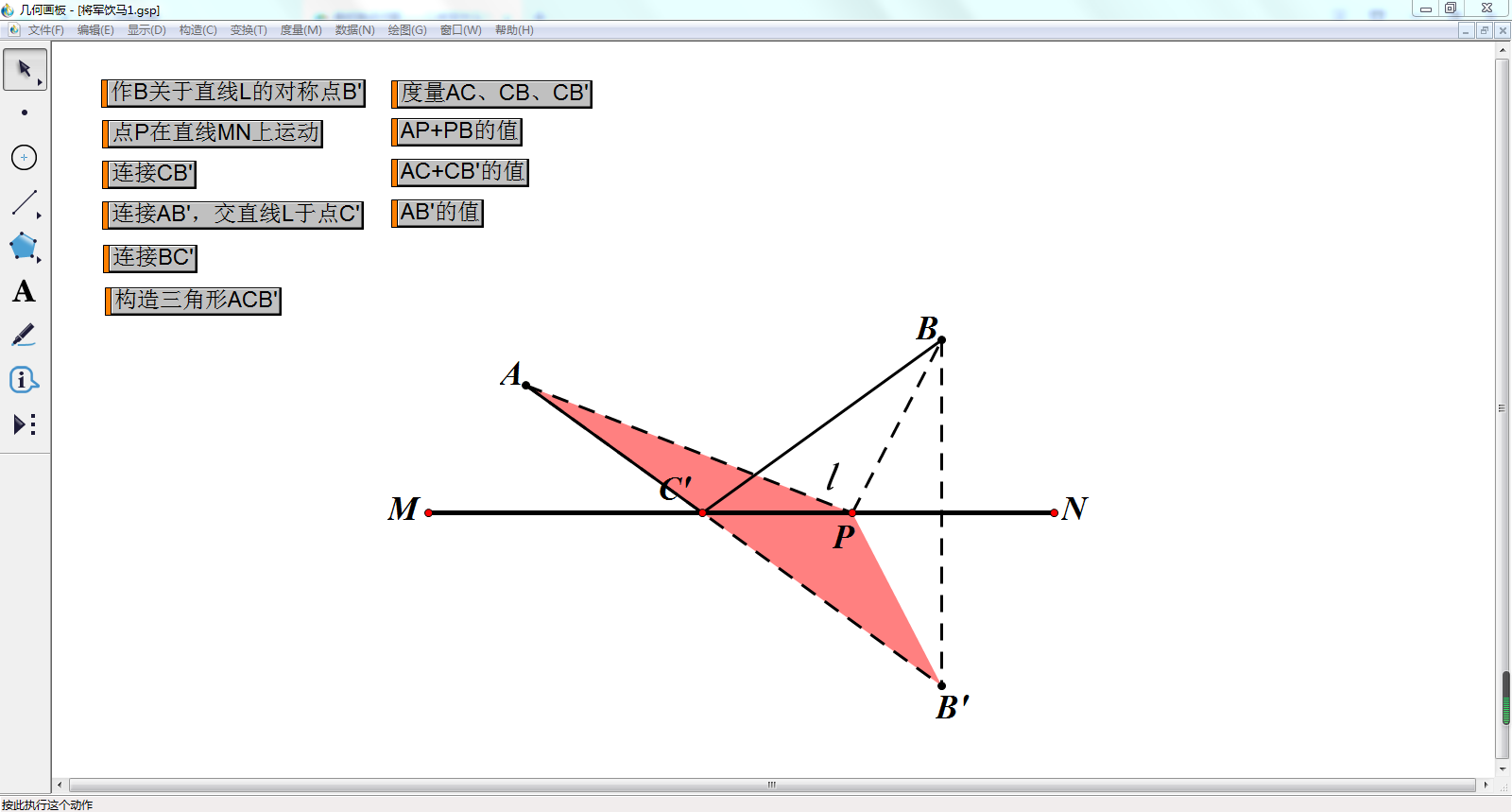
设计意图:利用多媒体课件几何画板的动态功能,让学生更直观的想象P点的运动轨迹,通过观察AP+BP值的大小变化,让学生自己总结出P点存在的唯一性
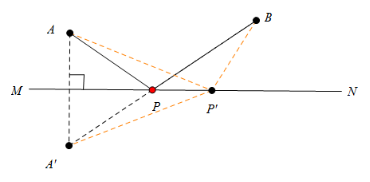
作法:
(1)作点B关于直线MN的对称点B′
(2)连结B′A,交MN于点C;点C就是所求的点;
解决方法:利用两点之间线段最短可以得到最短路径。
设计意图:由浅入深,让学生先理解两点在直线两侧情况中的最短路径问题。
实战演练1:例1变式1:已知:P、Q分别在是△ABC的边AB、AC上的点,你能在BC上确定一点R,使△PQR的周长最短吗?
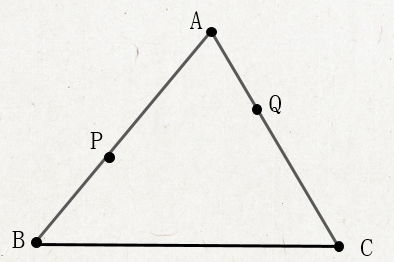
设计意图:让学生掌握用轴对称解决最短路径异侧到同侧的转化,并且学会用这种方法解决两定一动这一类的路径最短问题。
例1 变式2:如图,在等边△ABC中,边BC上的高AD=4,点P是高AD上的一个动点,E是边AC的中点,在点P运动的过程中,存在PE+PC的最小值,则这个最小值是 .
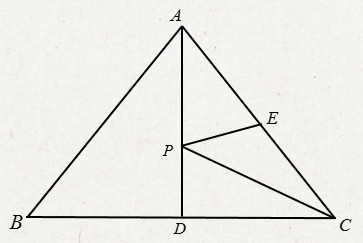
设计意图:让学生通过前面问题的探究解决两动一定最短路径的模型,并总结这一类题目解决的方法。
例2.如图:一位将军骑马从驻地A出发,先牵马去草地OM吃草,再牵马去河边0N喝水,最后回到驻地A,
问:这位将军怎样走路程最短?
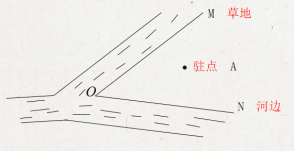
答案:
(1)作点A关于OM、ON的对称点A′、A′′
(2)连结A′和A′′,交OM于B,交ON于C则点B,C为所求.
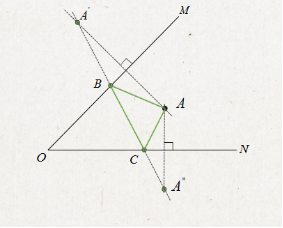
设计意图:让学生掌握用轴对称解决最短路径异侧到同侧的转化,并且学会用这种方法解决两定一动这一类的路径最短问题。
同学们谈谈这节课运用了哪些数学知识,你们学到了什么?
(1)本堂课解决了什么问题?
(2)解决最短路径之将军饮马问题的关键是什么?依据是什么?方法是什么?
设计意图:有效小结,总结提升。分层分维度小结,发散思维,实现螺旋式上升。
必做题:课时作业
选做题:
如图,∠AOB=30°,在内有一点P,且OP=6,点M、N分别是OA、OB上的动点,则△MNP周长的最小值为 .
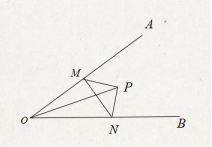
设计意图:温故知新,及时复习。分层作业实现人人学有用的数学,不同的学生得到不同的发展。
最短路径问题——以将军饮马为例
异侧问题 现学现用 1

同侧问题 学生上台板书

验证:AP'+P'B>AP+PB 演示学生的练习实战演练2
因为AP+PB=A'B 又AP'+P'B>A'B
即有AP'+P'B>AP+PB
所以AP'+P'B>A'B
设为正确答案