- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课是学生在学习了三角形的基本概念、全等三角形的性质和判定及轴对称性质的基础上,进一步探索特殊的三角形——等腰三角形性质的第一课时.本节内容既是前面知识的深化和应用,又为证明角相等、线段相等、直线垂直提供了方法,也是后续学习等边三角形、菱形、正方形、圆等内容的重要基础,具有承上启下的重要作用.等腰三角形是轴对称图形,它的其它性质是借助这个性质来探究的.等腰三角形性质的探索与证明体现了转化的思想,掌握好本节内容对数学问题的解决有着积极的意义.
从认知基础上,学生在小学对等腰三角形已经有了初步的认识.在初中阶段,学生慢慢的学会了通过观察、操作、猜想这样一个过程来接受新的知识,也经历了全等三角形的逻辑推理论证过程,积累了一些推理论证的经验.但学生接触用数学符号表示推理的时间不长,将文字命题转换为符号语言还不熟练,逻辑思维能力和运用几何语言进行正确表达的能力还有待提高
从学习心理上,八年级学生活泼好动,表现欲望强烈,但是学生对于几何推理、归纳总结的能力还比较弱,思维的广阔性、灵敏性比较欠缺.学生习惯了解题能解出来就行,绝不多想,不注重反思和思维的优化.
(一)知识与技能
掌握等腰三角形的性质,会运用性质进行有关的证明和计算。
(二)过程与方法
1.经历等腰三角形性质的探索和证明过程,体会轴对称在研究几何问题中的作用。
2.通过运用等腰三角形的性质解决相关问题,发展应用意识,培养分析解决问题的能力.
(三)情感态度与价值观
1. 让学生感受建筑的宏伟,培养学生乐于观察,并会用数学的观点看待问题的能力。
2. 经历同学间的合作交流,培养学生团结协作、乐于助人的品质。
3. 规范几何语言和解题格式,使学生养成良好的学习习惯。
教学重点:等腰三角形性质的探索、证明及其应用.
教学难点:性质1证明中辅助线的添加和对性质2“三线合一”的理解.

1. 欣赏图片,激发兴趣.
用多媒体播放生活中精美的建筑物图片,引导学生进入学习情境,发现图片中的几何图形——等腰三角形.
2. 联系生活,问题引入.
为什么在盖房子时工人师傅用等腰三角板检测房梁是否水平?利用中学生好奇的心理,调动学生的学习积极性.
3. 直奔主题,板书课题.
让我们一起走进等腰三角形的世界,去探索其中的奥秘!(板书——等腰三角形)
(设计意图:用生活中的图片创设情境,引导学生观察、联想,让学生感受到我们生活中的数学无处不在,并学会从数学的角度去观察事物, 思考问题, 激发学生对学习数学的兴趣,调动学生的学习积极性.)
1. 剪一剪
(播放微课视频)学生动手操作,在准备好的长方形纸片上裁剪出一个等腰三角形,教师与学生一起动手折纸,剪纸,标好字母并演示,选剪得好的三角形进行展示 .

(设计意图:让学生利用轴对称性剪出等腰三角形,为等腰三角形的性质探究作准备.视频的使用,让学生明确目的,剪一个规范又美观的等腰三角形,方便学生后面的观察和性质的探究)
2.猜一猜
教师提问:请同学们把手中的等腰三角形沿折痕对折,找出其中重合的线段和角,你能猜一猜等腰三角形有什么性质吗?小组成员相互交流.
学生独立思考,把剪出的等腰三角形纸片沿折痕对折,找出其中重合的线段和角,并与小组成员互相交流.然后积极举手跟全班分享所发现的结论,说出自己的猜想.教师引导学生观察、完善、归纳出等腰三角形的性质1和性质2.
(设计意图:观察——猜想——验证是研究几何图形中非常常见也是非常重要的思维方式,设计这一环节,旨在培养学生这一思维方式.让学生通过等腰三角形的轴对称性发现其它性质,动手操作,直观感知,经历由特殊到一般的过程,在反复比较的过程中发现等腰三角形的性质,培养学生的抽象概括能力.突出以学生为主体,引导学生互动合作探究学习.)
3.证一证
(1) 证明猜想1:等腰三角形的两个底角相等.
教师提问:对于这样一个文字命题的证明有哪些步骤?
教师引导学生用多种方法进行证明(经过学生思考,讨论交流可能会出现四种证法:三种做辅助线构造全等的方法及证等腰三角形与它本身全等),学生积极思考,并在学案上独立完成对猜想1的证明,积极参与小组讨论和交流,踊跃上台来展示自己的成果并认真倾听同学的讲解,若发现问题积极主动地纠正,对没听懂的问题主动向讲解的同学提出,由讲解的同学负责解答,教师纠正和补充学生发言,投屏展示学生的证明方法,板书性质1及几何语言.
教师进一步总结:这条性质为我们在一个三角形中证明角相等提供了新的方法.
(2)由性质一推出等腰三角形底角的平分线、腰上的中线、腰上的高互相重合
教师提问:刚才证性质一的时候我们用了哪几种作辅助线的方法?
(作底边上高 作顶角平分线 作底边中线)
教师提问:底边上高、顶角平分线、底边中线这三者之间有什么关系?
(等腰三角形底角的平分线、腰上的中线、腰上的高互相重合.PPT动画展示三线重合的过程.
教师追问:“为什么呢?”引导学生对上述证明结果进行再分析,发现这也间接地证明了猜想2,就得到性质2.
教师提问:一般三角形有这个性质吗?(不具有) 教师使用几何画板直观演示
继续提问:当它变形成什么三角形时就可能具有呢?
教师使继续用几何画板直观演示等腰三角形底角的平分线、腰上的中线、腰上的高并提问为什么变成等腰三角形后也不互相重合呢?学生回答后,教师再使用几何画板直观演示“三线不合一”到“三线合一”过程,发现三线合一的条件,再拖拽改变等腰三角形的两腰大小,“三线合一”现象依然存在.可以让学生自己上台感受操作几何画板,感受这个变化过程.
接下来教师引导学生剖析性质2,理解其含义.
①等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高.
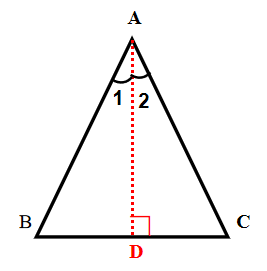
几何语言:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)
②等腰三角形的底边上中线,既是底边上的高,又是顶角平分线.
几何语言:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2(等腰三角形三线合一)
③等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线.
几何语言:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2(等腰三角形三线合一)
(3)由对性质一和性质二的证明推出等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴.由学生说出等腰三角形的对称轴
(设计意图:以学生为主体,让学生通过自主学习,合作探究证明等腰三角形的性质,从而达到获取知识,提升能力的目的.几何画板的使用,让学生直观地观察图形的变化,进一步验证了自己探究出的性质的正确性,加深对性质的理解和识记.此外,性质2的理解是本节课的难点,学生往往认为等腰三角形的中线、角平分线和高都互相重合或三角形中出现某一线就有三线合一,这个时候利用几何画板直观感受,教学效果会很明显.)
1. 解决情境引入中的问题
为什么工人师傅用等腰三角板检测房梁是否水平?学生思考后举手回答.
(设计意图:让学生学会把生活中的实际问题构建成数学模型,解决数学模型从而解决生活问题.让学生感受数学源于生活,应用于生活.)
2. 小游戏:比比谁更快.用希沃白板5的课堂活动环节做了一个小游戏,男女生各派一个代表来PK,游戏时间的设置恰当,让学生有一种紧张情绪在,同时学生的错误也能提醒注意:(1)别看知识点好像认识了,但在运用中不一定能得心应手;(2)审题必须认真,避免发生不应该的错误.
(设计意图:考虑到上课已有一段时间,学生的注意力已经开始分散,设计小游戏让学生立马兴奋起来,在放松的同时检测学生知识点掌握情况.这一课堂活动旨在调动课堂气氛,让学生玩中学,学中玩.)
3. 典例精析
例1 如图,在∆ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求∆ABC各角的度数.
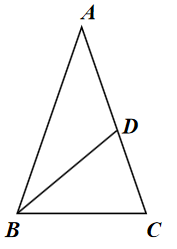
学生讨论完成并上台展示 ,师生共同评价并总结解题方法和其中蕴含的数学思想.
例2 已知: 如图,点D、E在∆ABC的BC边上,AD=AE,AB=AC,
求证:BD=CE.
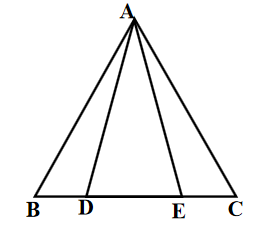
组织讨论,引导学生分析,重点让学生意识到等腰三角形中的“三线合一”常常作为解决等腰三角形问题的辅助线,“转化”是我们解题的重要策略.
(设计意图:及时巩固所学知识,检测反馈学习效果,树立学生的自信心,为学生搭建一个展示自己才华的平台的同时培养学生正确应用所学知识的能力,增强应用意识.例1“黄金三角形”中体会方程思想,例2的教学充分让学生讨论和交流,进行一题多解的训练,有效地培养了学生的发散思维能力.从几种方法的证明中让学生感知等腰三角形“三线合一”性质在解决问题中的应用,体会到利用等腰三角形性质解题可以大大简化证明过程.注重引导学生从一题一解到一题多解,最后到一题优解,让每个层次的学生都有收获,同时激发学生的竞争意识,在小组内比,在小组间比,也能培养团队合作意识.)
学生畅谈收获,回顾梳理这一节课的内容,交流感受和体会.课件上展示这节课的知识框架,让学生形成良好的知识体系和认知结构.
(设计意图:通过小结,梳理一节课的收获,有利于学生形成良好的知识体系和认知结构,培养学生的归纳、反思能力.通过这个环节,教师总结本节内容的源与流,有助于学生全面地了解自己的学习过程,积累数学活动经验,感受自己的成长与进步,增强自信.)
在等腰三角形中,我们学习了“等边对等角”,在任意一个三角形中,如果是不相等的两条边,它们所对的角之间又有什么大小关系呢?
(设计意图:通过拓展提问,引导学生进一步思考,提升学生思维的深刻性.从等腰三角形的“等边对等角”到一般三角形的“大边对大角”和“小边对小角”,体现了数学中“从特殊到一般”的类比思想.还让程度高的学生把课堂中“实践-发现-猜想-证明”的探究过程运用到拓展中来,真正渗透数学思想方法,激发了学生的学习能力和兴趣.)
1. 必做题:自学预习课本77、78页内容,自主构建本节课的知识网络,课本77页练习题第1、3题;82页第2题.
2. 选做题:如图:∆ABC中,AB=AC, AD和BE是高,它们相交于点H,且AE=BE.
求证:AH=2BD.
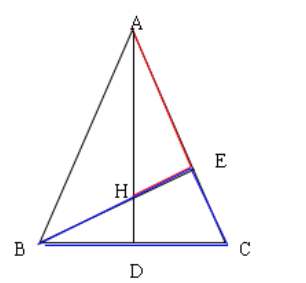
设为正确答案