- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



六年级上册数学教材P107-P111为数学广角《数与形》单元,例1为以形解数,例2以数助形,练习课前3题为配套练习,从第4题开始,题目的范围逐渐拓展,不再局限于例题的配套练习。数与形相结合的例子在整个小学阶段无处不在,本节课为数与形整理与复习课,所以需将整个一年级上册至六年级上册(共11册)的内容整理,并大概分为四个模块:概念,运算、解决问题 和其他。
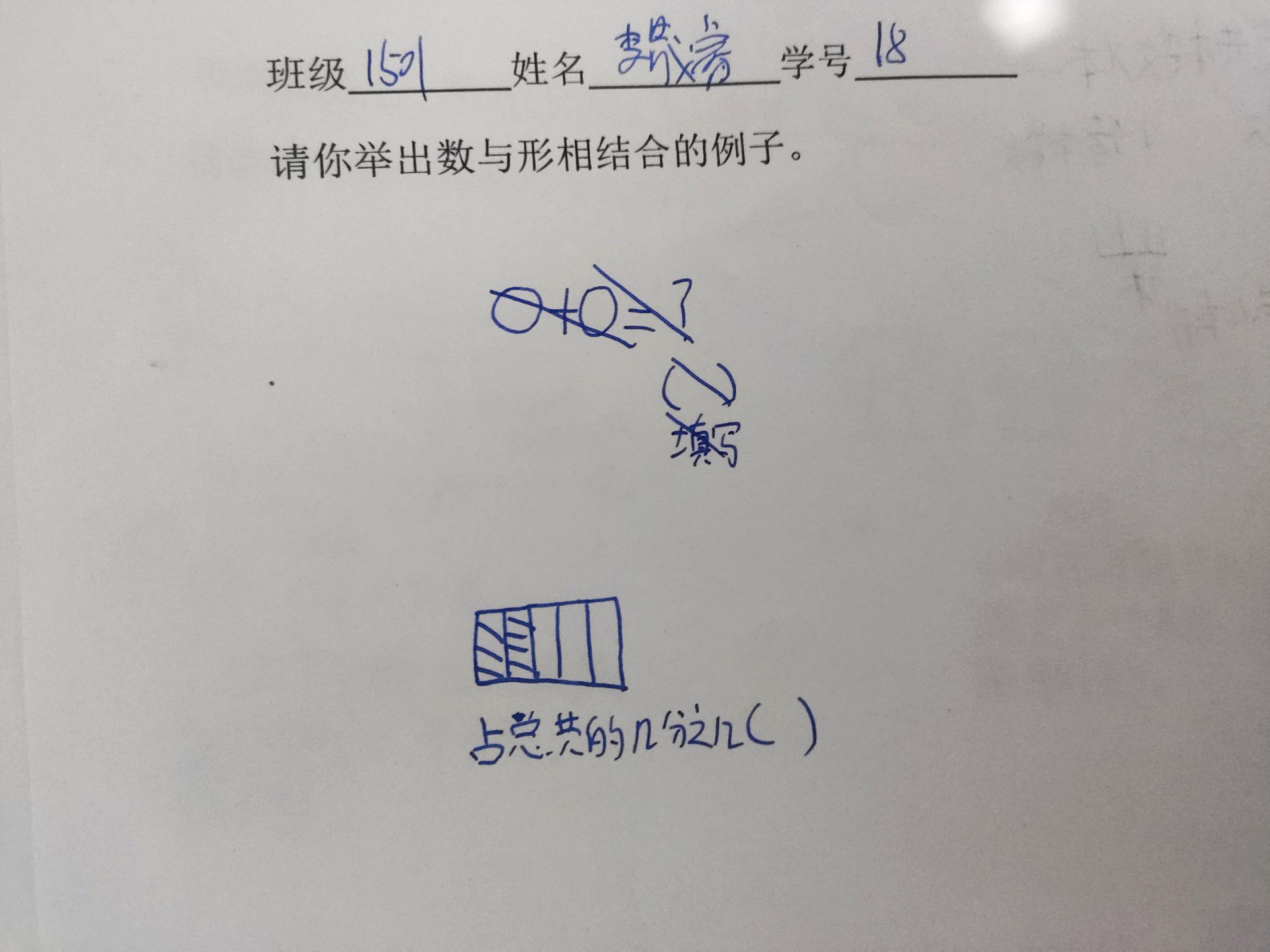
学生在小学阶段已经接触到了很多数与形相结合的例子,学生也能举出各种各样的例子,不过是零散的,没有集中起来系统地分成几个板块,为了了解孩子们对于数与形结合的掌握程度,所以我们制作了课前调查,请学生举出数与形相结合的例子。
1、让学生通过课前举出数与形相结合的例子,回顾以往知识,自行整理归纳,自主研究发现数的问题可以借助图形来理解,形的问题可以用数来计算。
2、使学生会利数形结合的方法来解决探究题。
3、使学生在解决数学问题的过程中,体会和掌握数形结合、归纳推理等基本的数学思想。
教学重点: 引导学生在整理与复习的过程中理解数与形之间的关系,发现数与形关系密切,互帮互助,无处不在。
教学难点:结合教学内容,使学生在问题解决的完整过程中体验数与形的相互作用,实现数形认识上的跨越。

一、导入
著名数学家华罗庚对数与形的关系说过这样一段话,请大家齐读:‘’
数缺形时少直觉,形缺数时难入微。数形结合百般好,隔离分家万事休。
‘’
谁来说说这几句话是什么意思?
二、新授
昨天我们做了一张课前小调查,让所有同学举出你认为是数与形相结合的例子。让我们来看看同学们举出来的例子吧!
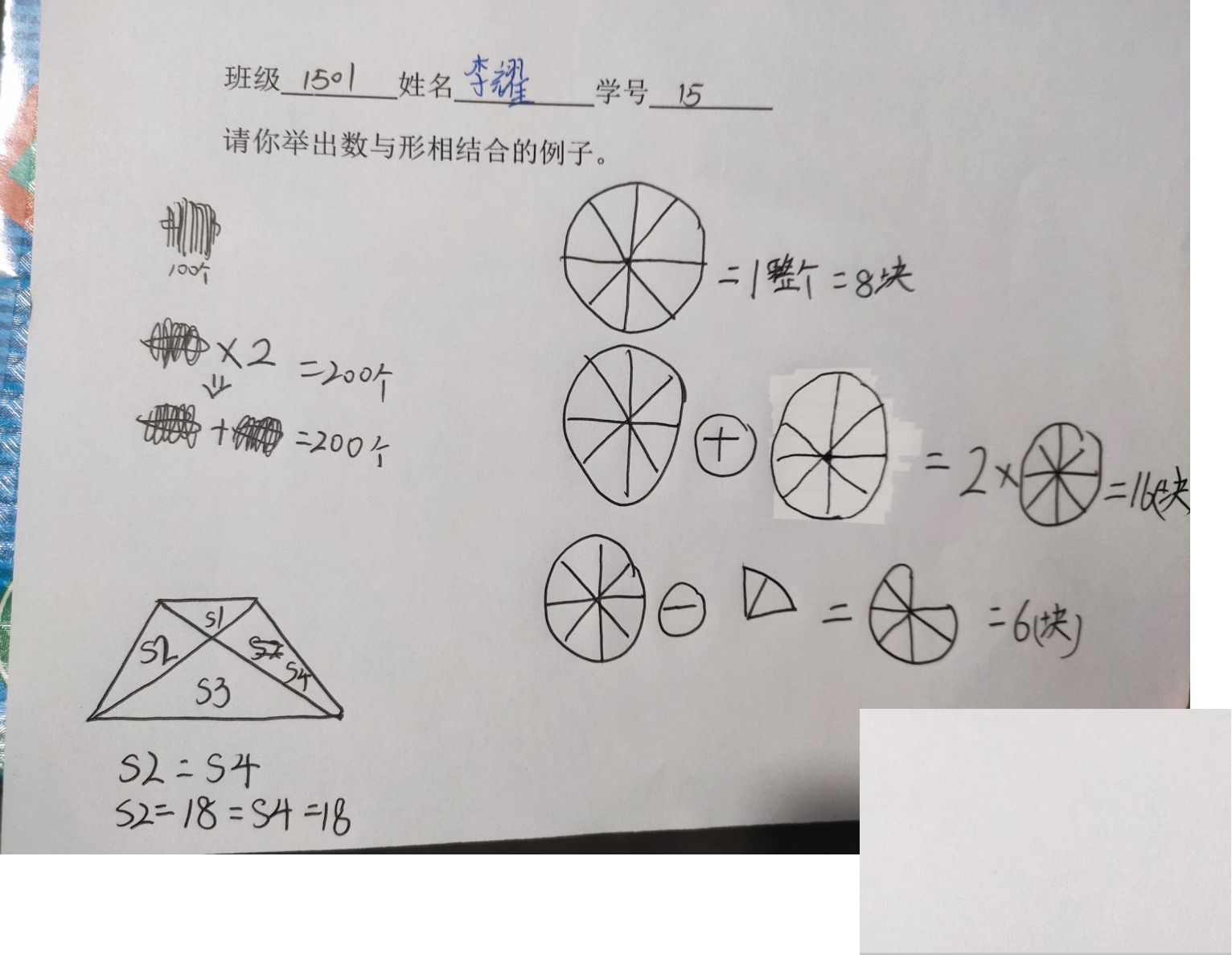
1、出示学生概念中的数与形例子:
请学生解释:




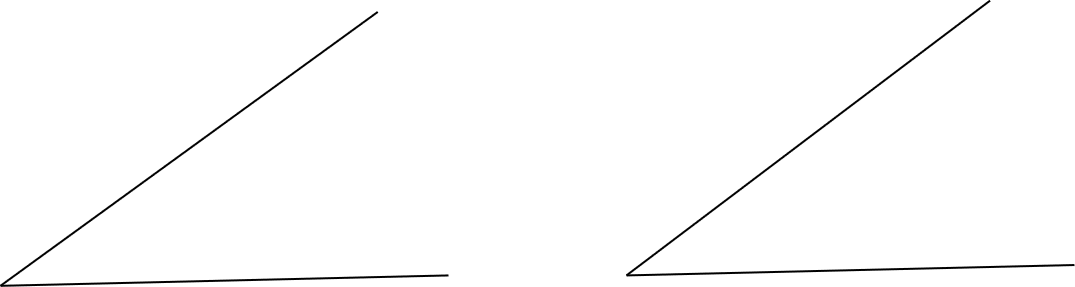
师:当两个角差不多,肉眼无法看出哪个角大哪个角小的情况下,需要用到什么?
生:量角器。
师:使用量角器是想要量出什么?
生:这两个角的具体度数。
师:在对角进行分类时,我们用具体的数据衡量每个角的大小。
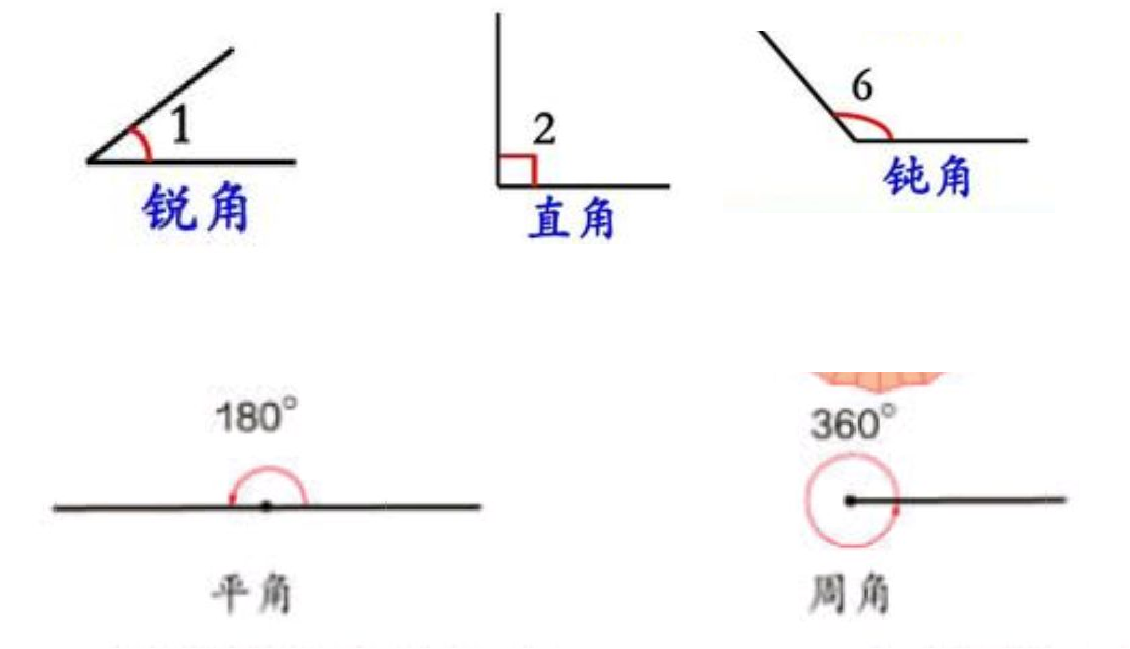
师:同学们还记得角是怎么分类的吗?
生:角可以分为锐角、直角、钝角、平角、周角。
师:还能说的再详细一点吗?
生:小于90度的角是锐角、等于90度的角是直角、大于90度的角是钝角、180度是平角、360度是周角。
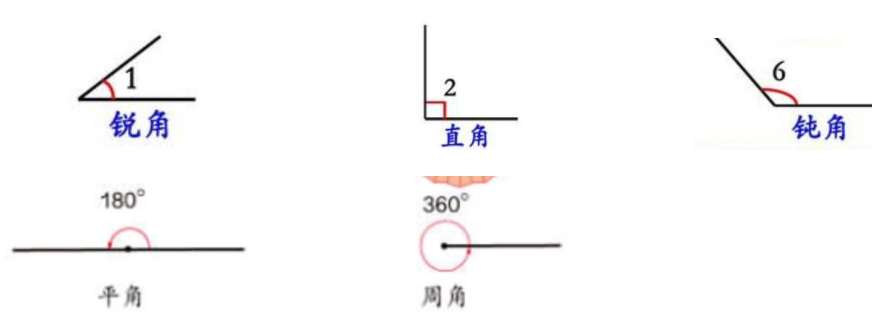
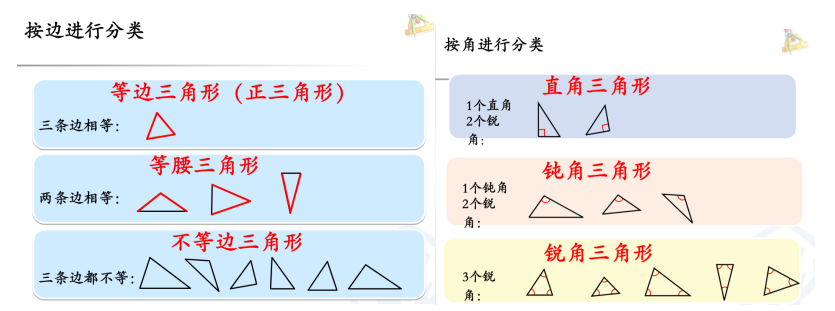
师:我们可以用“数”的测量与计算,准确地描述几何图形的性质。角因为有了度数,我们就知道它是什么角,如按最大角的大小可将三角形分成锐角三角形、直角三角形、钝角三角形;按边是否相等可分为等边三角形、等腰三角形、非等边三角形。
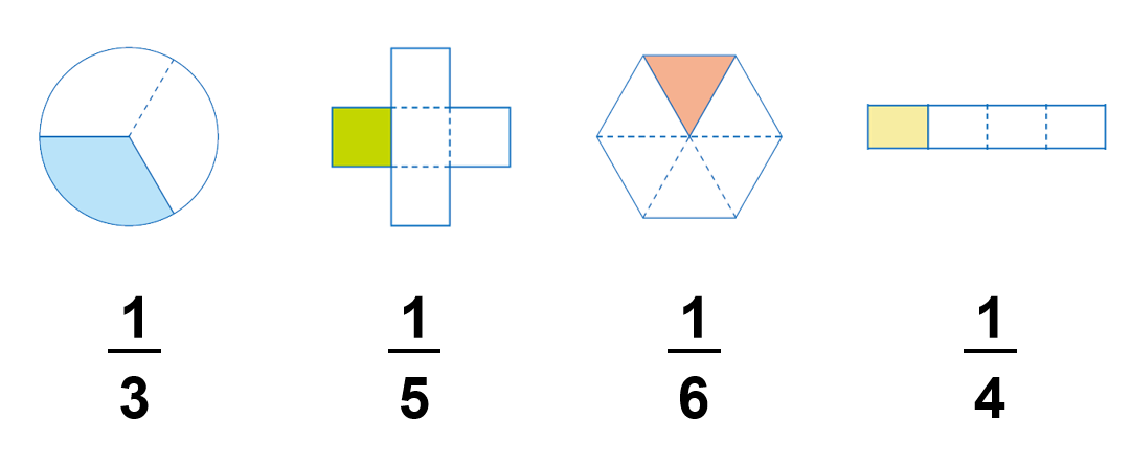
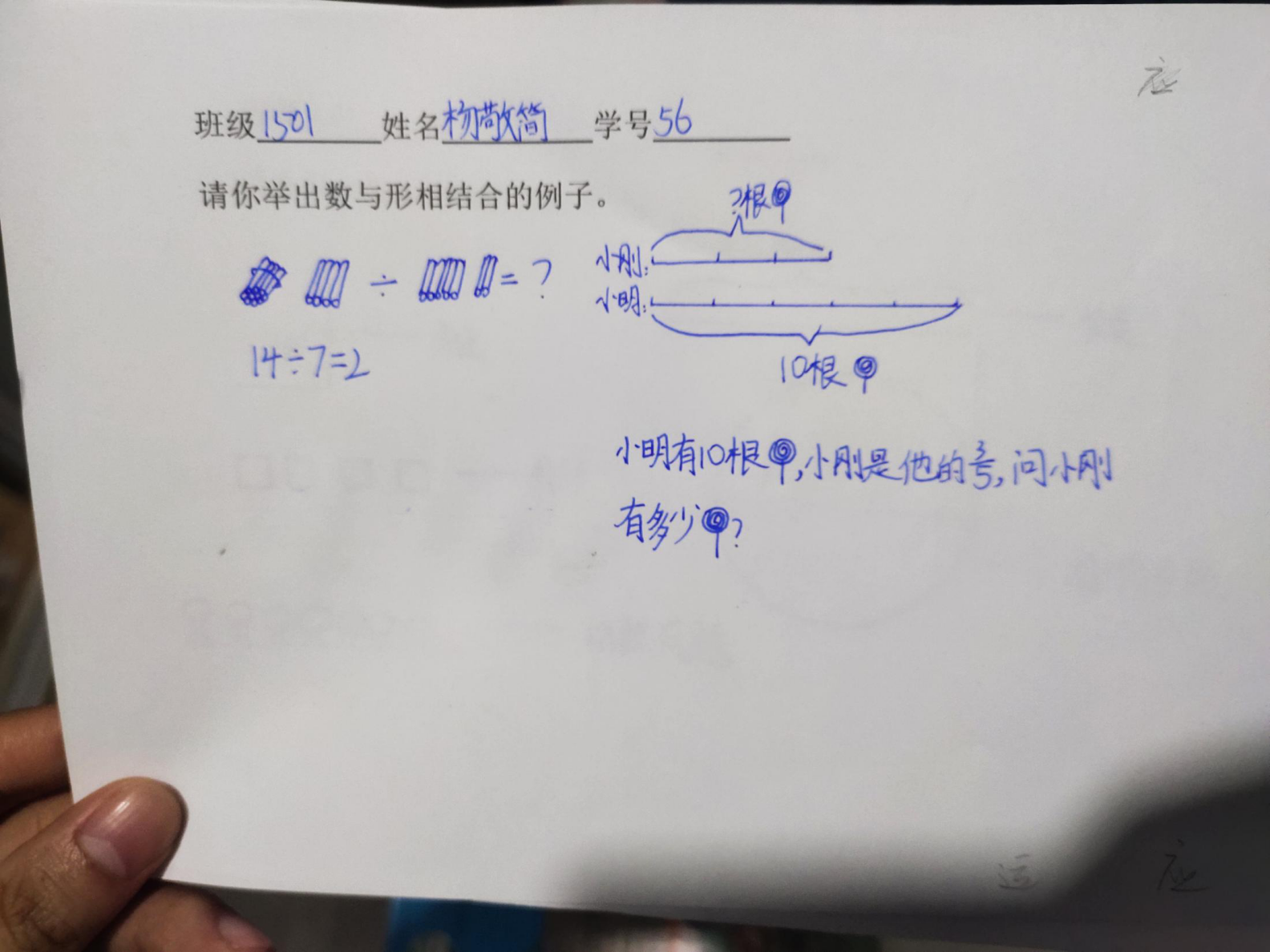
2、出示学生概念中的数与形例子:
请学生解释:
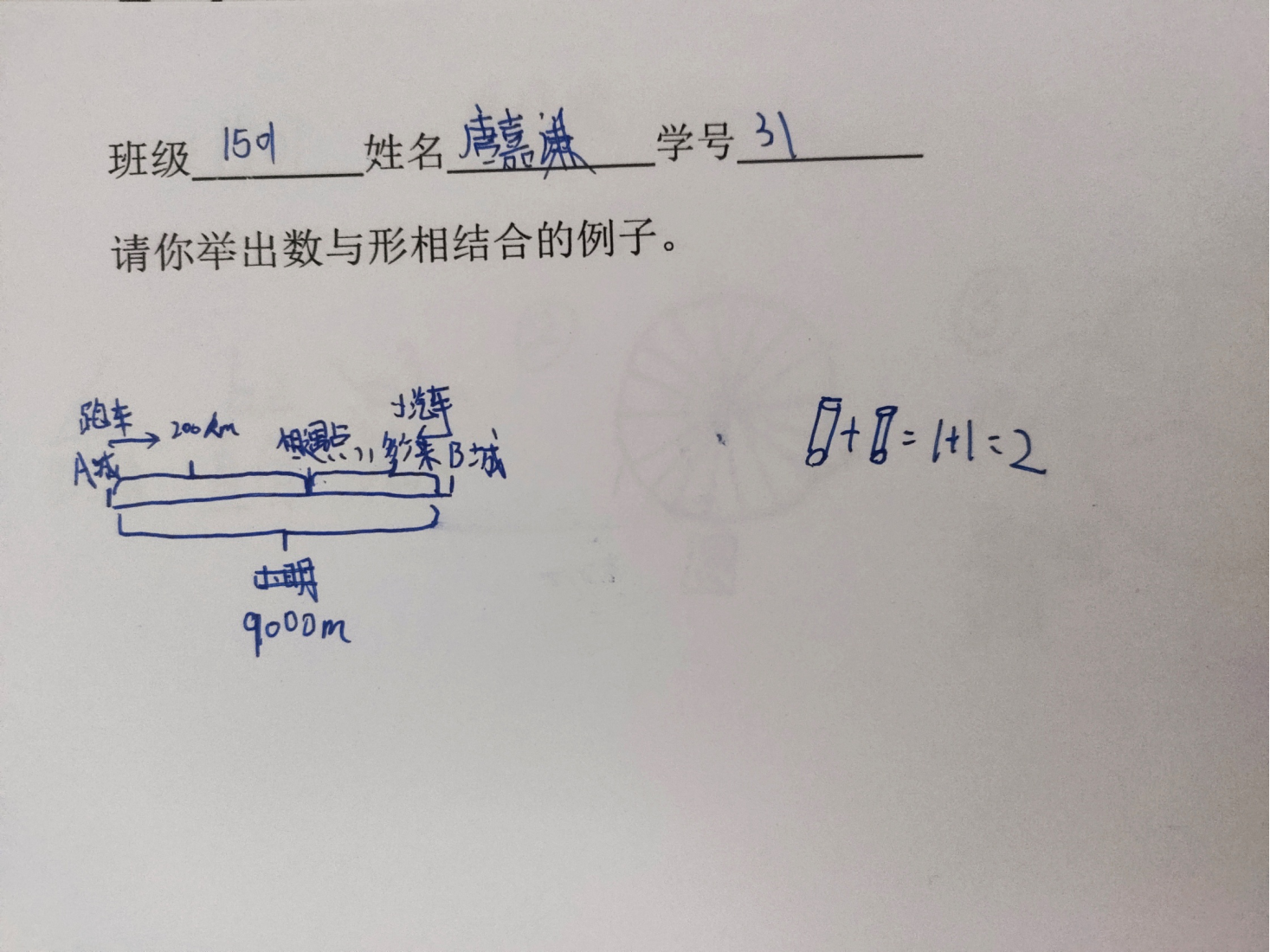
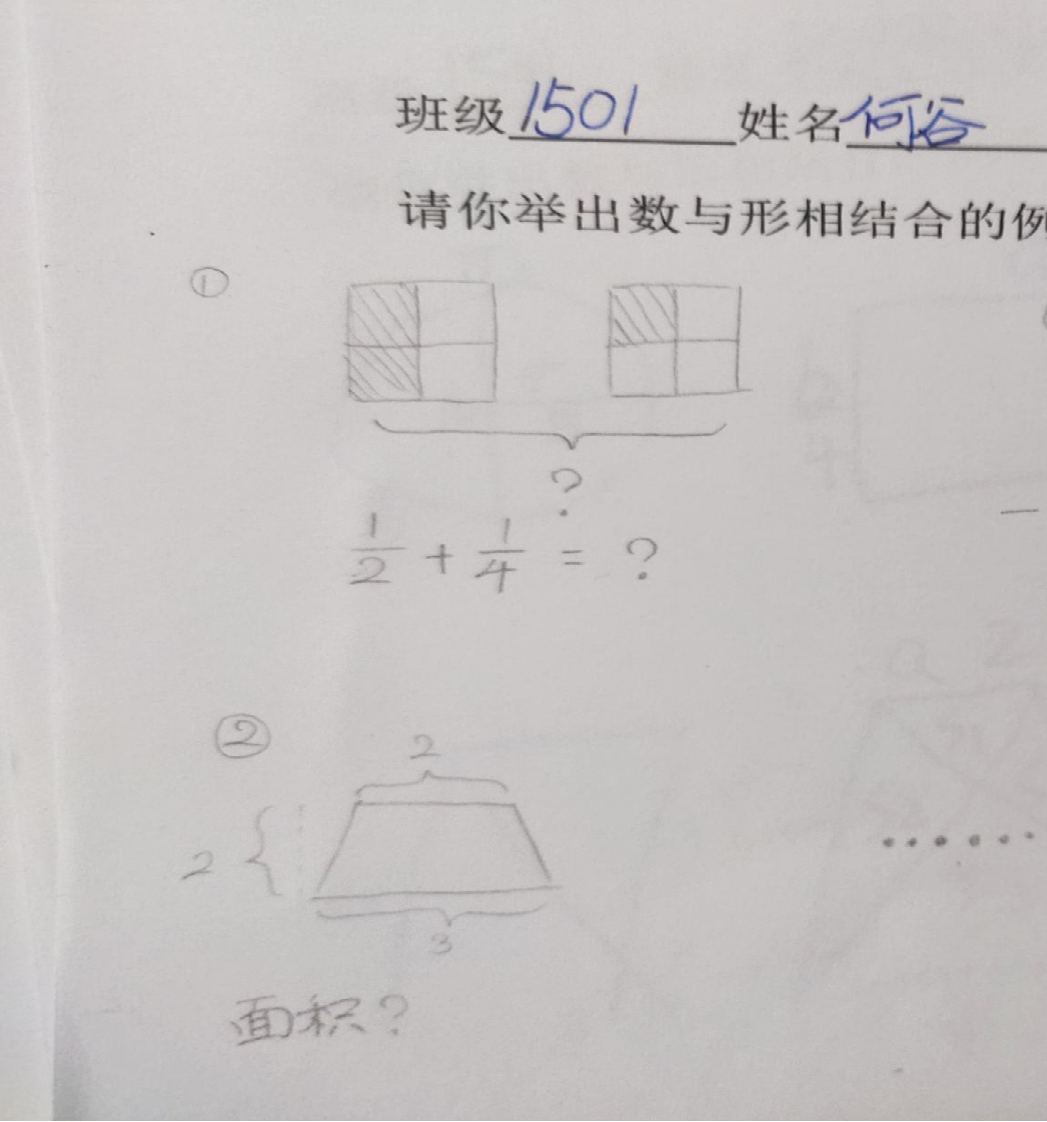

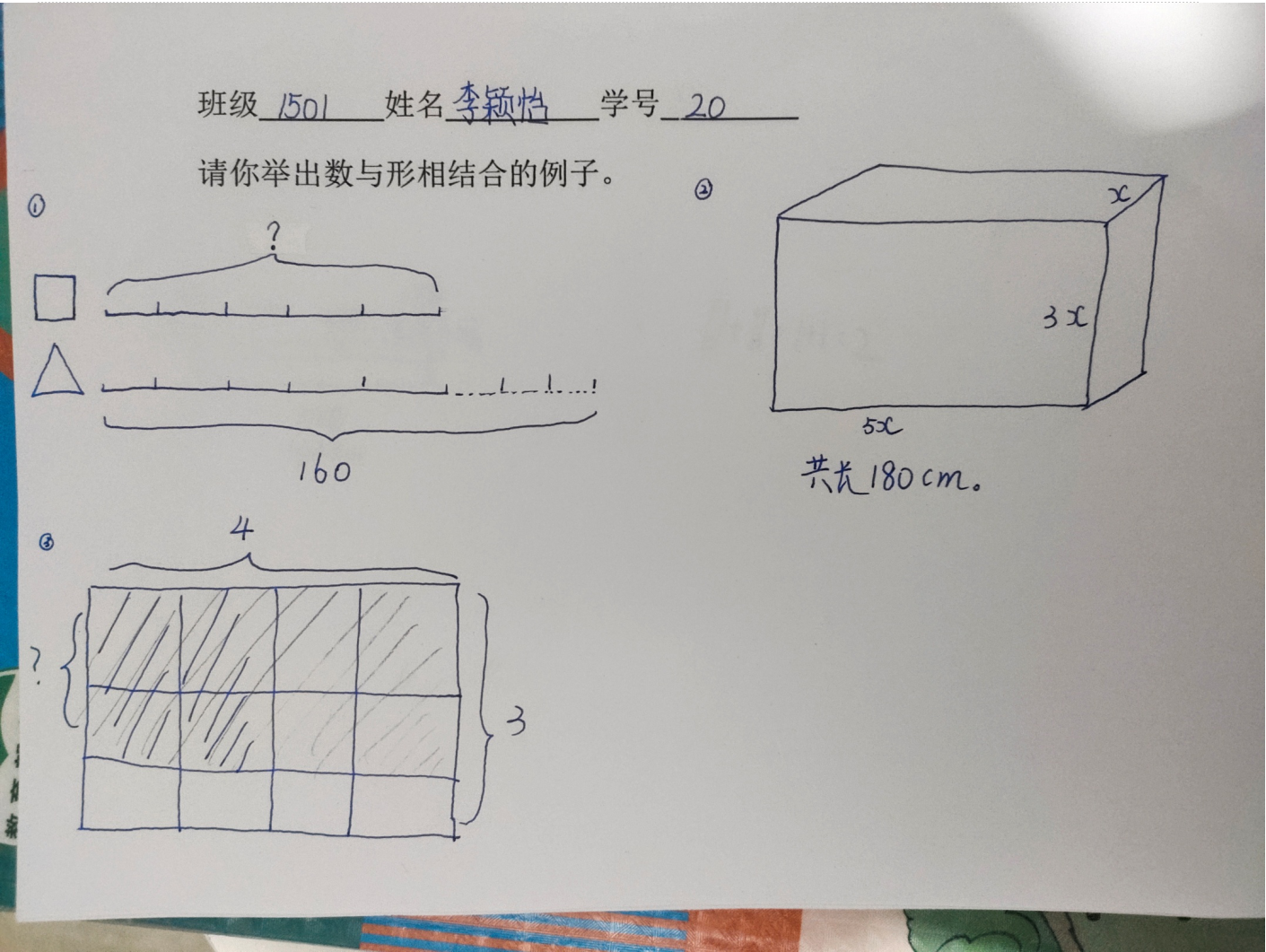
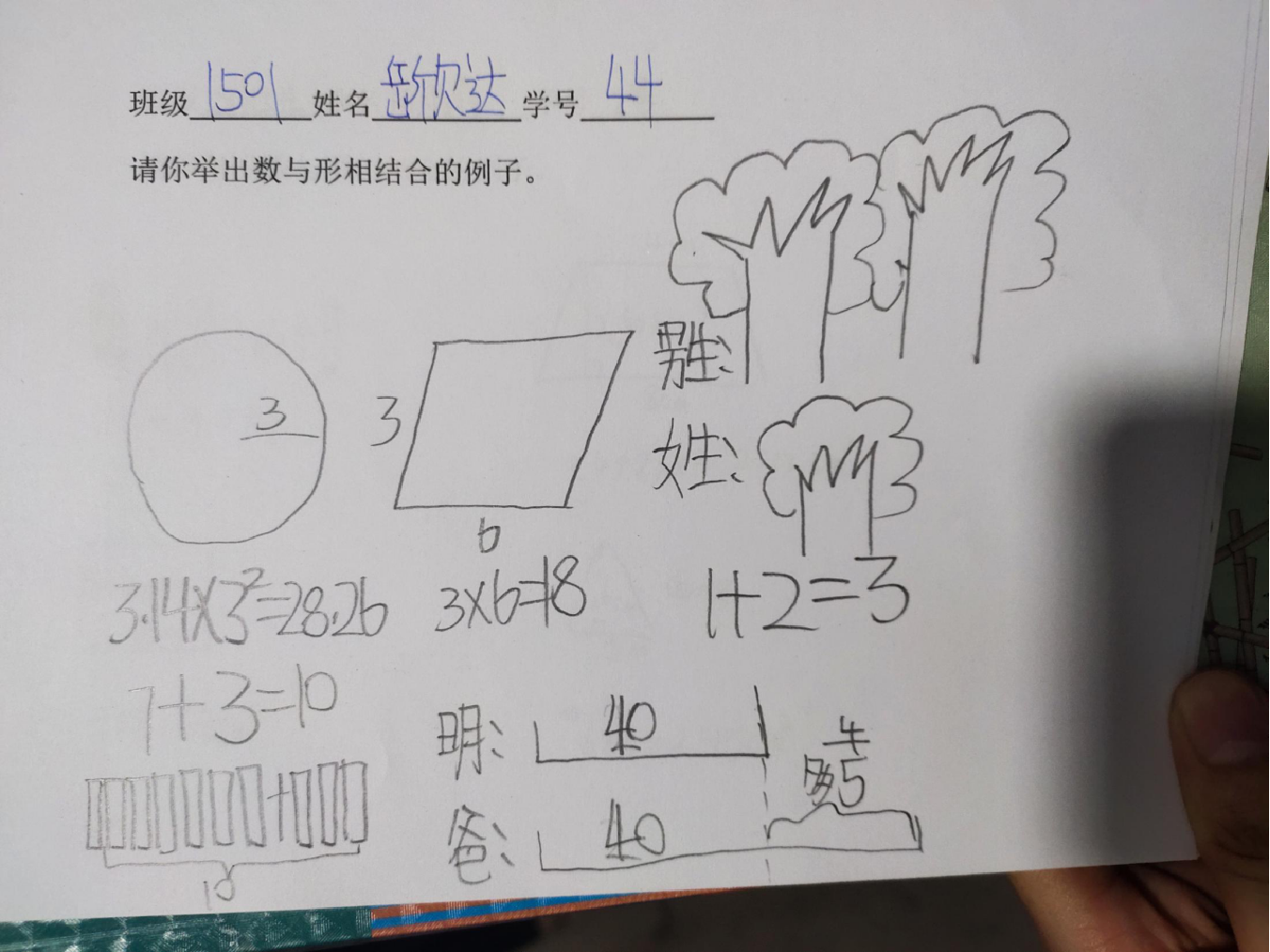
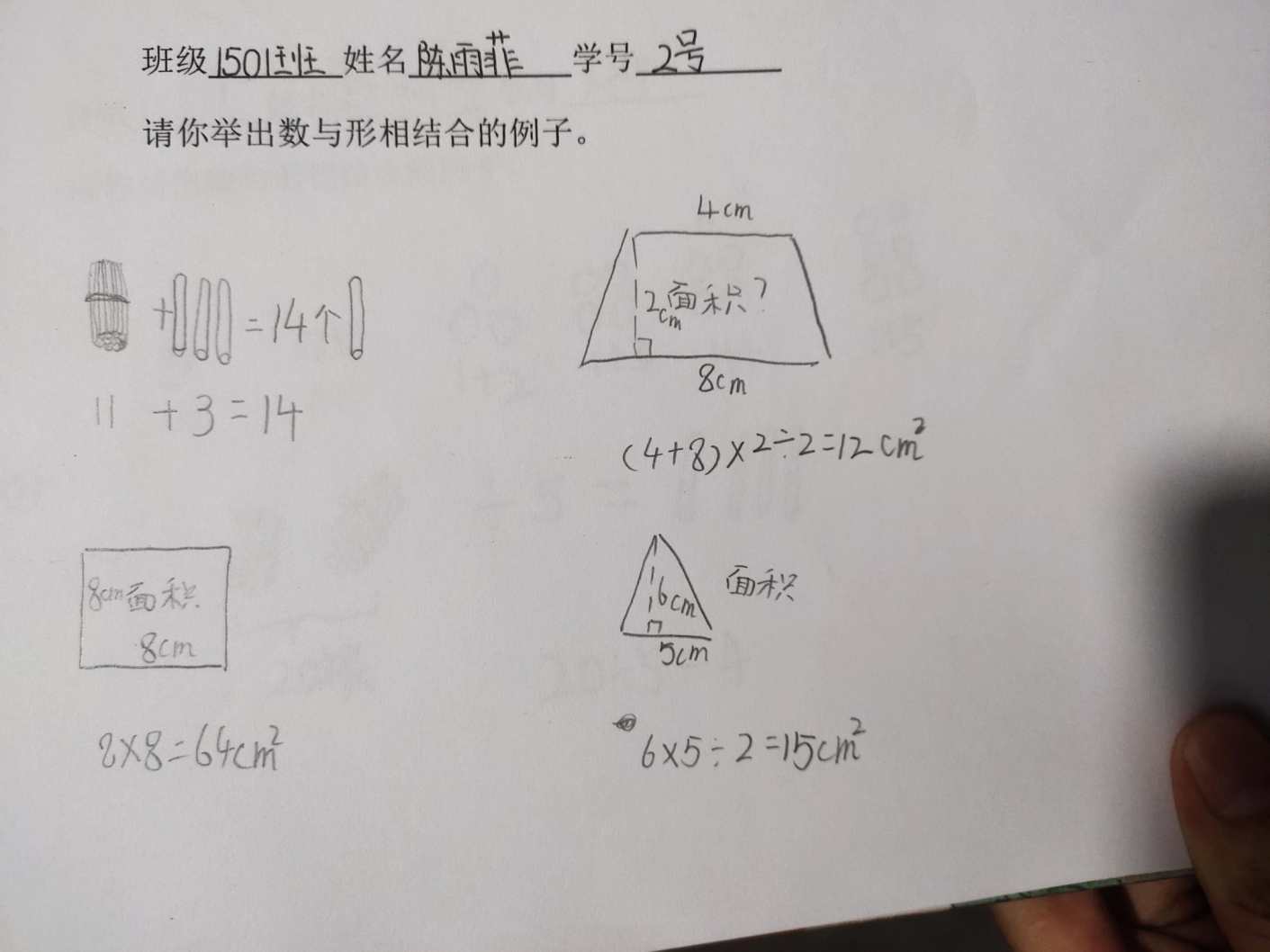
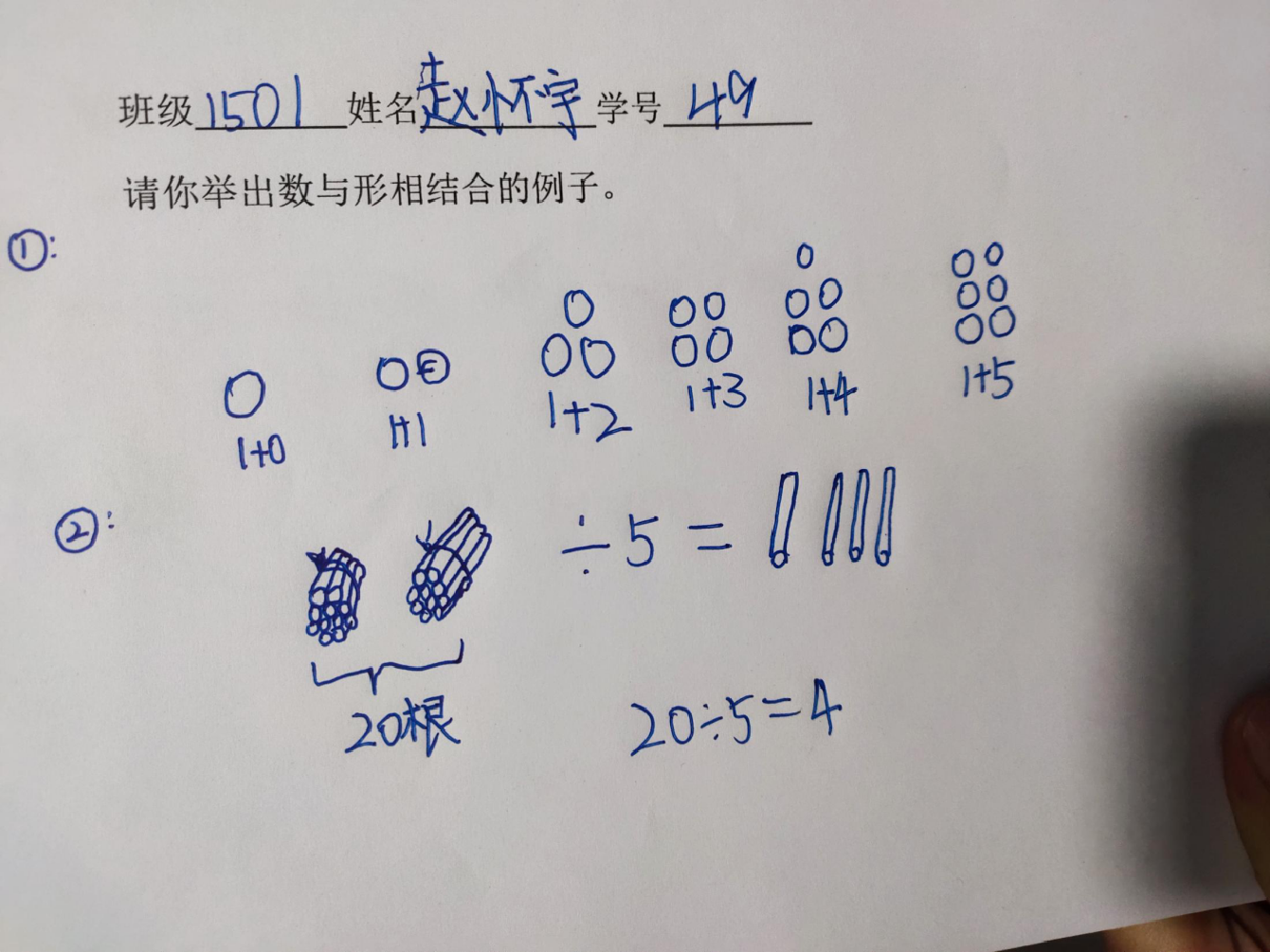

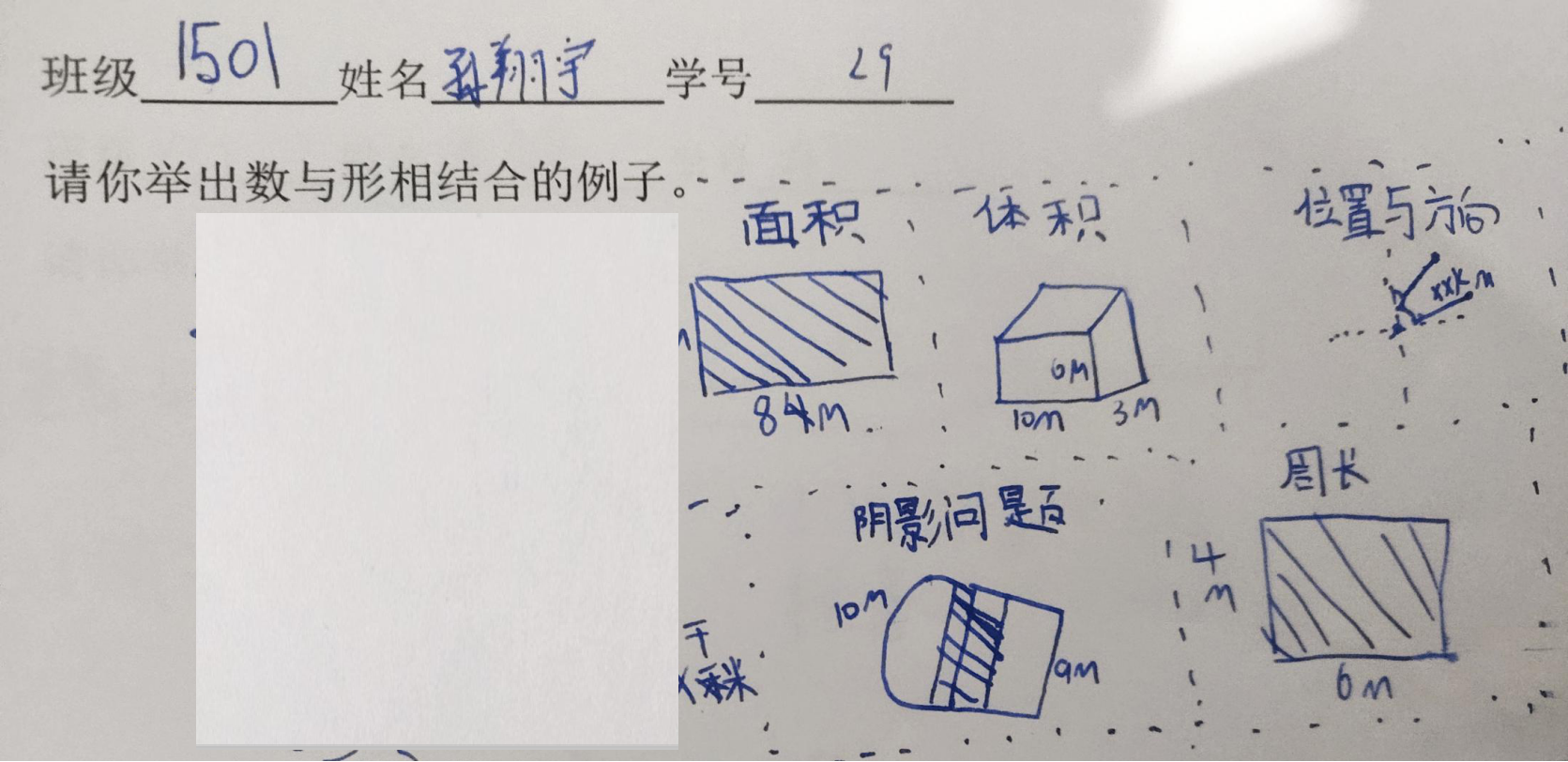
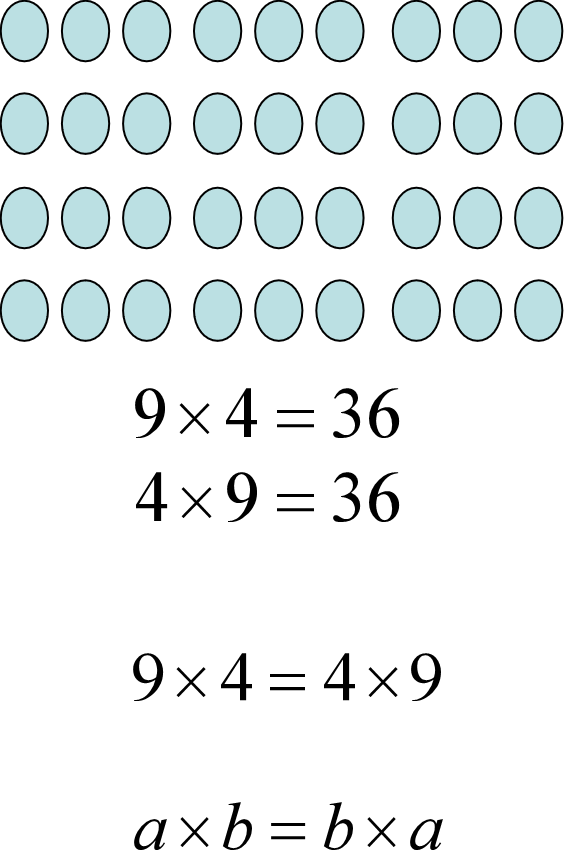
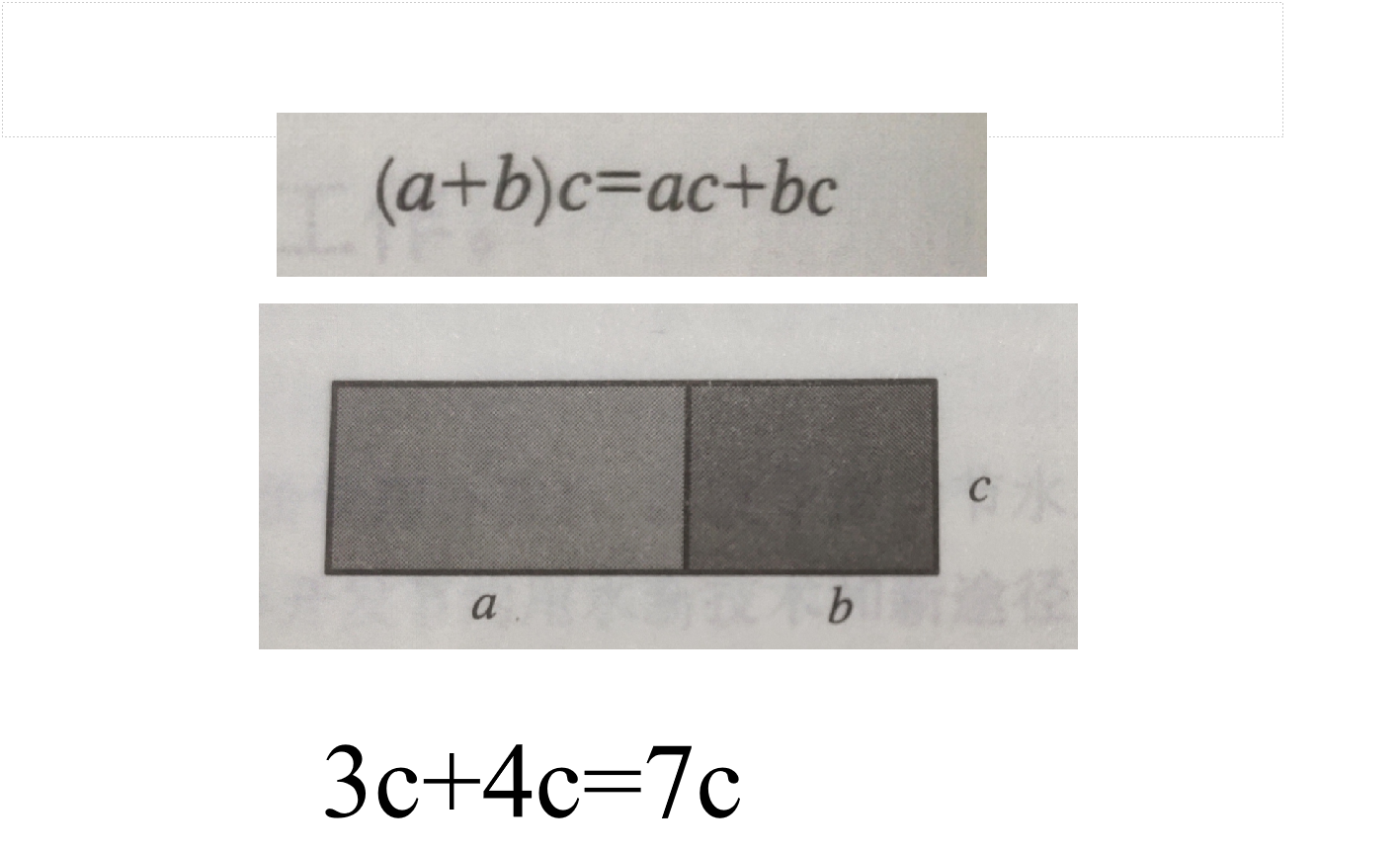
3、展示学生解决问题中的例子并请学生解释:


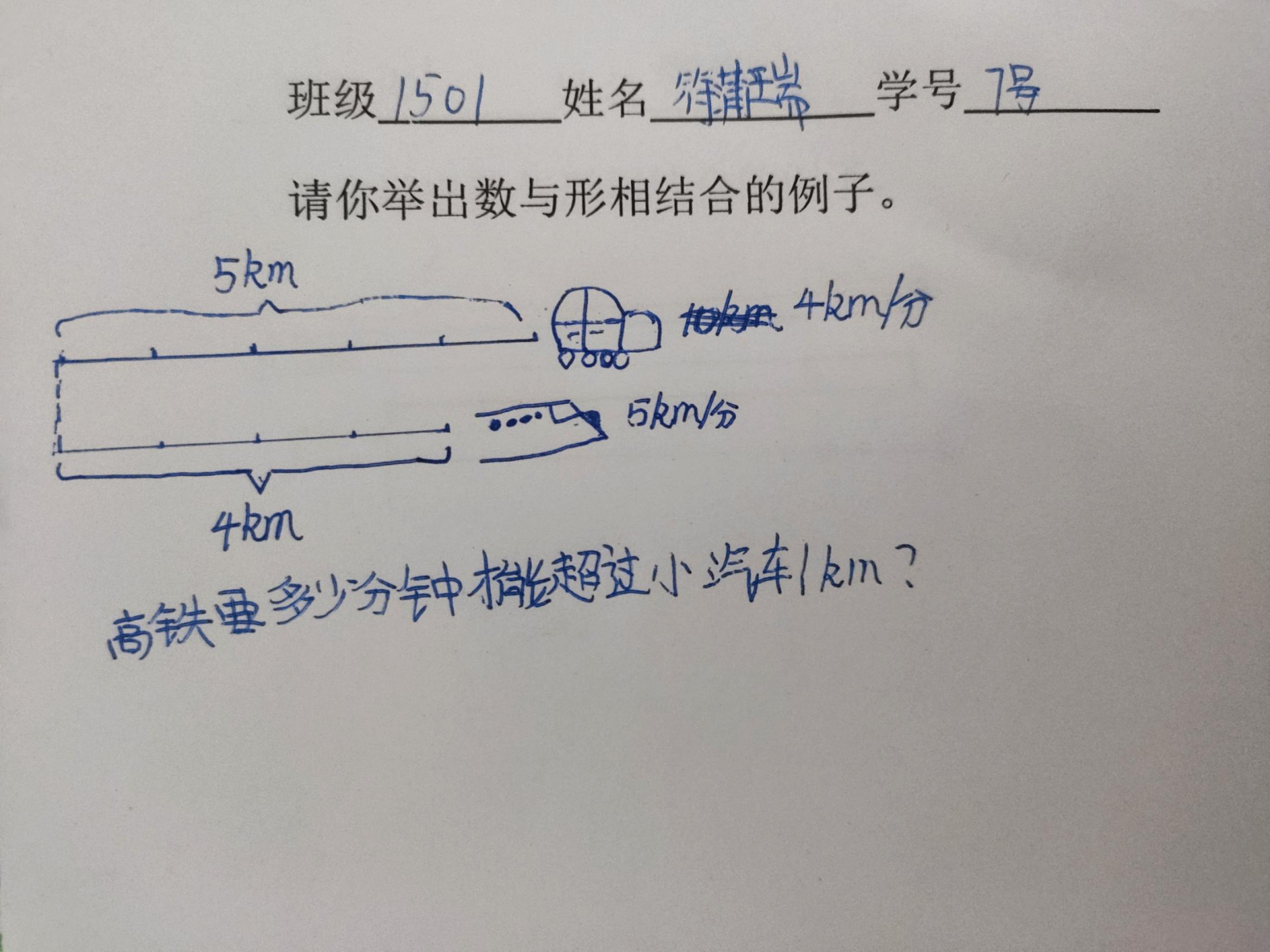
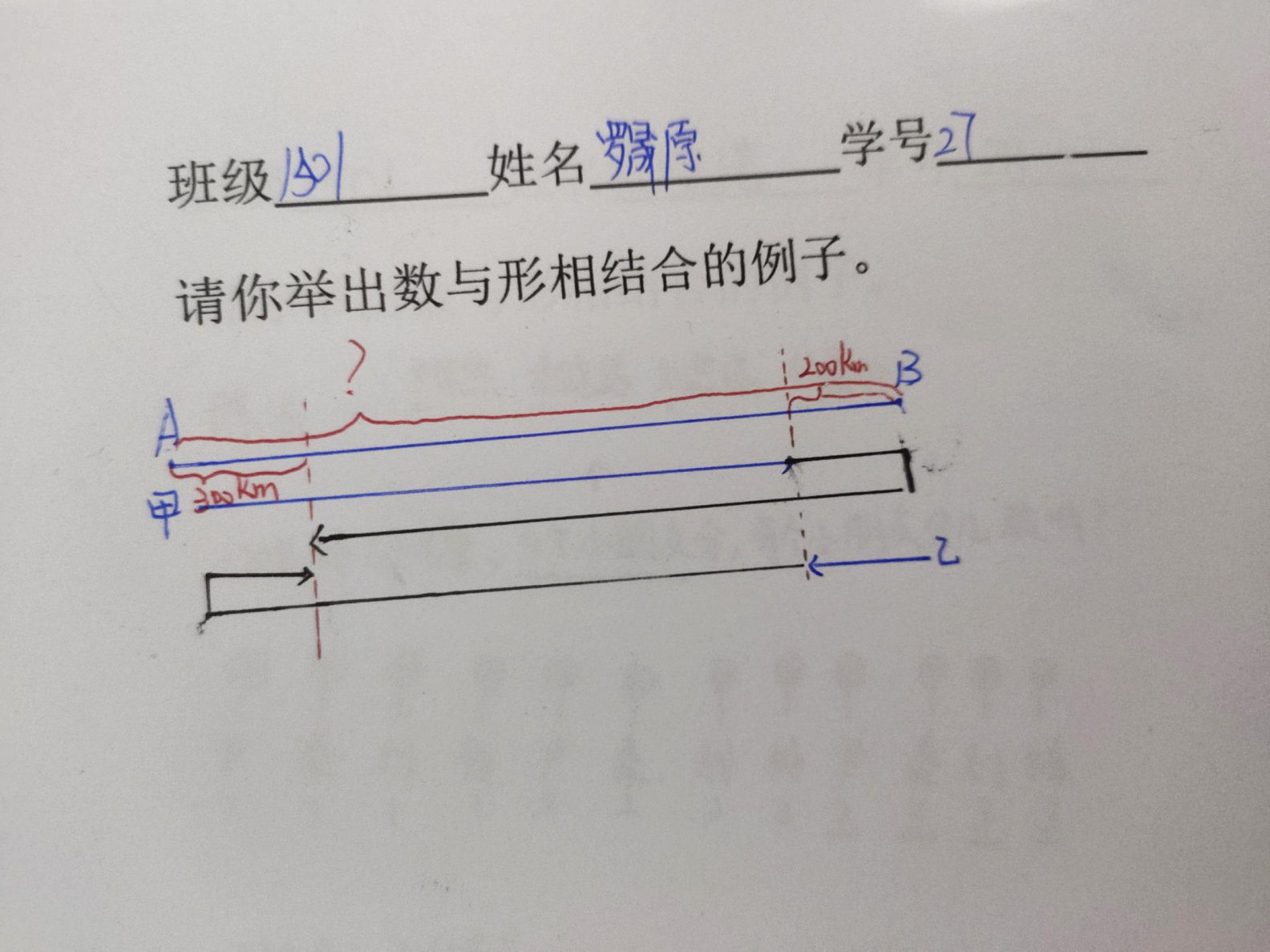

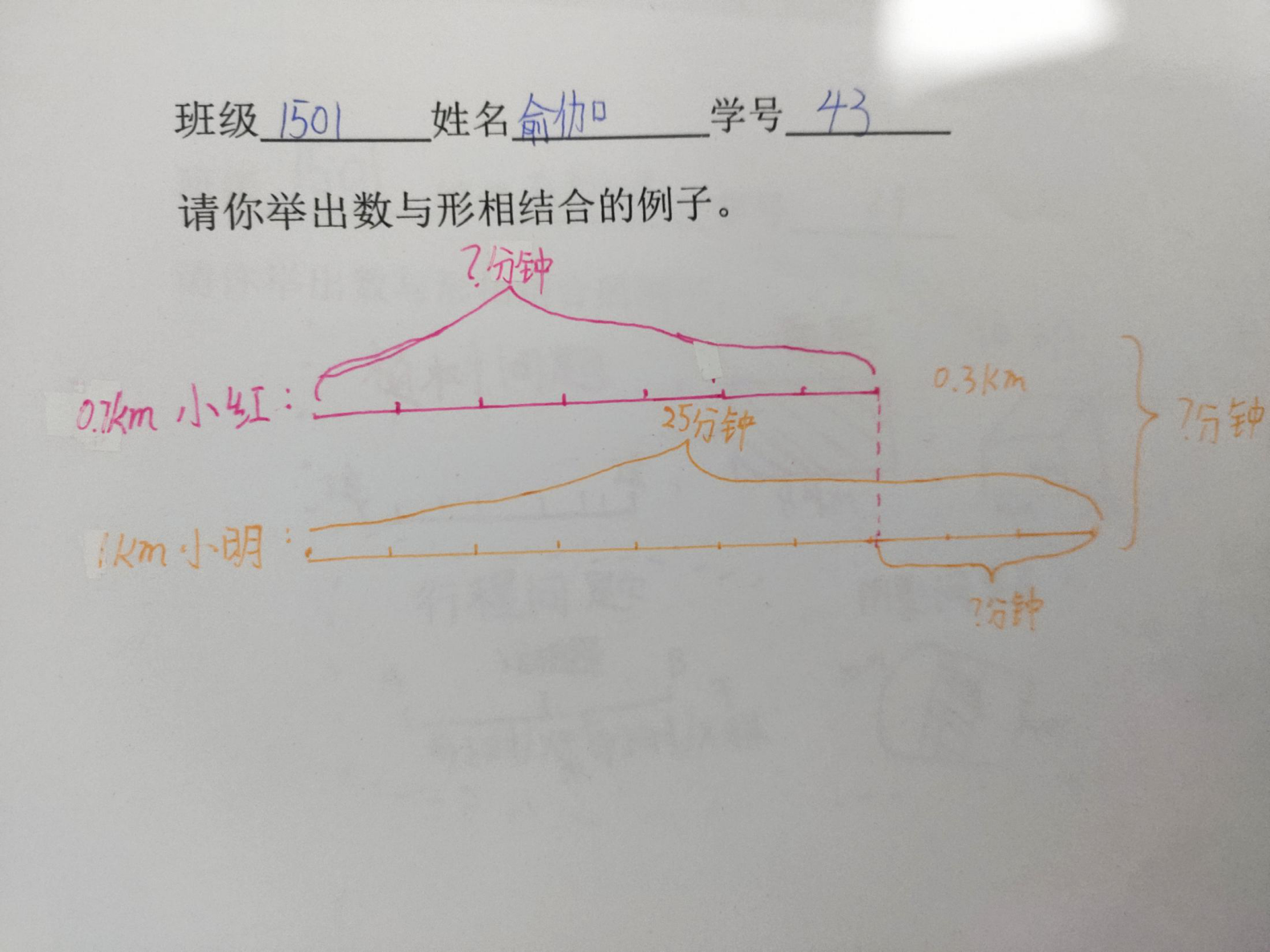

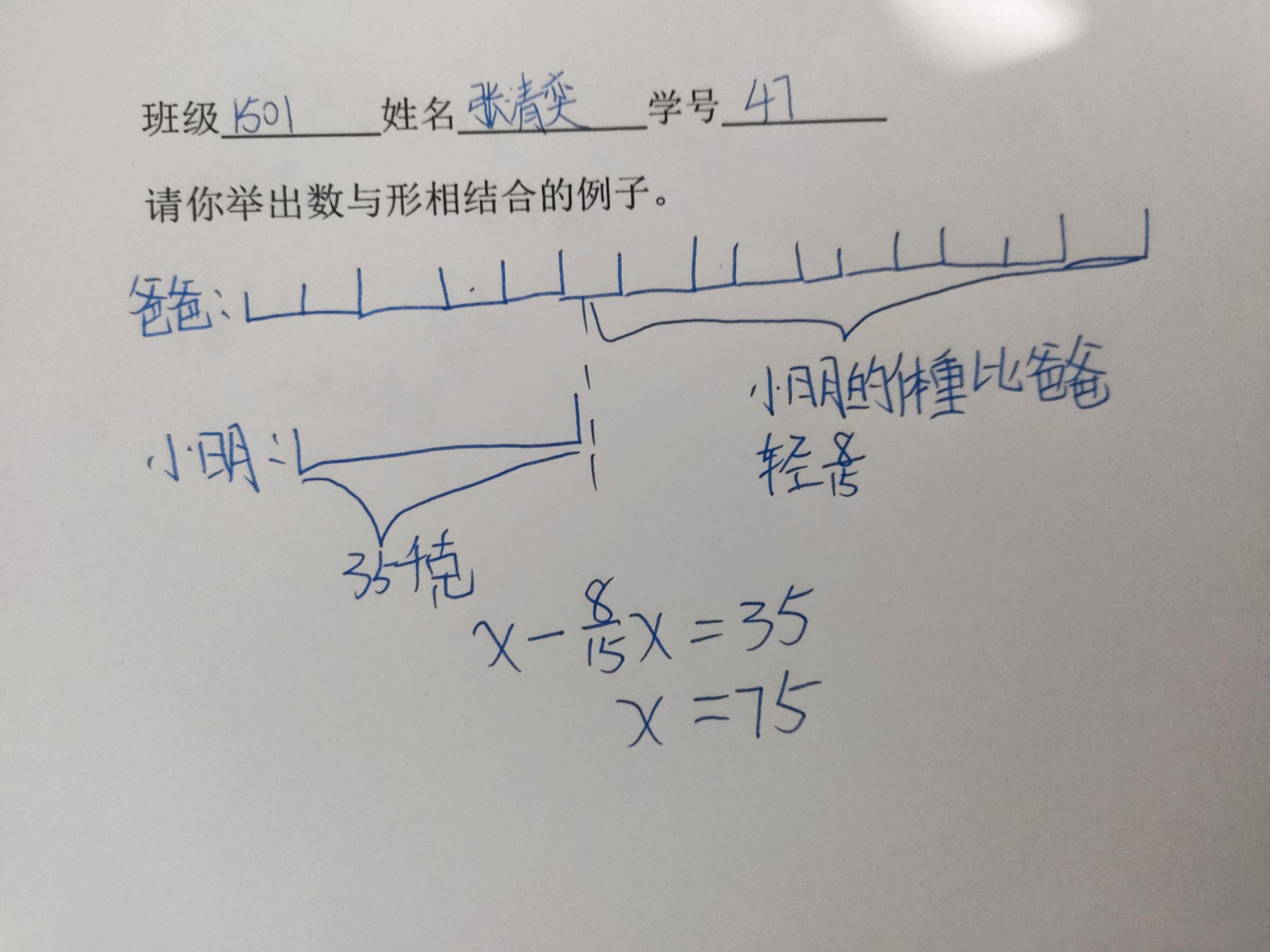

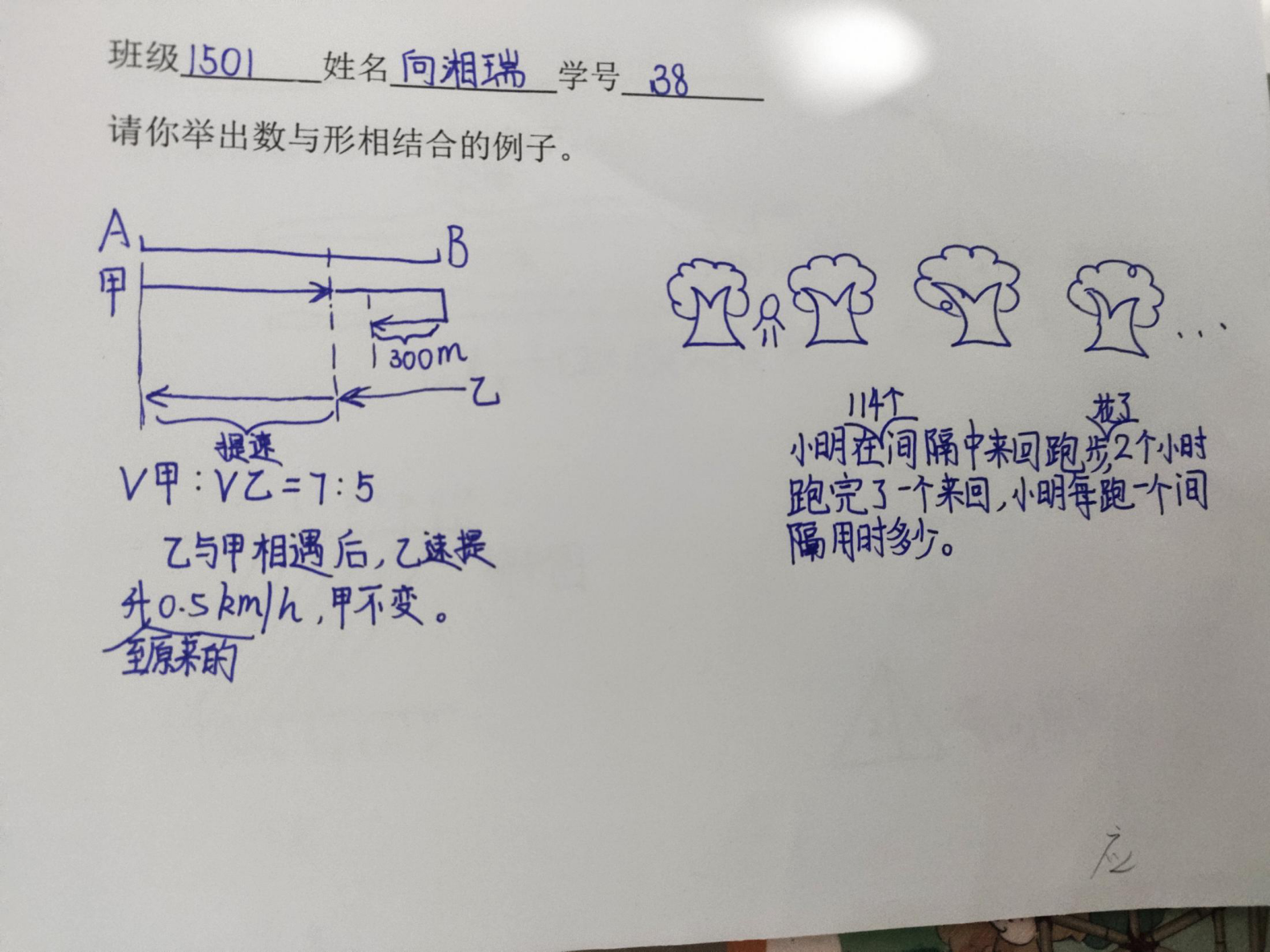

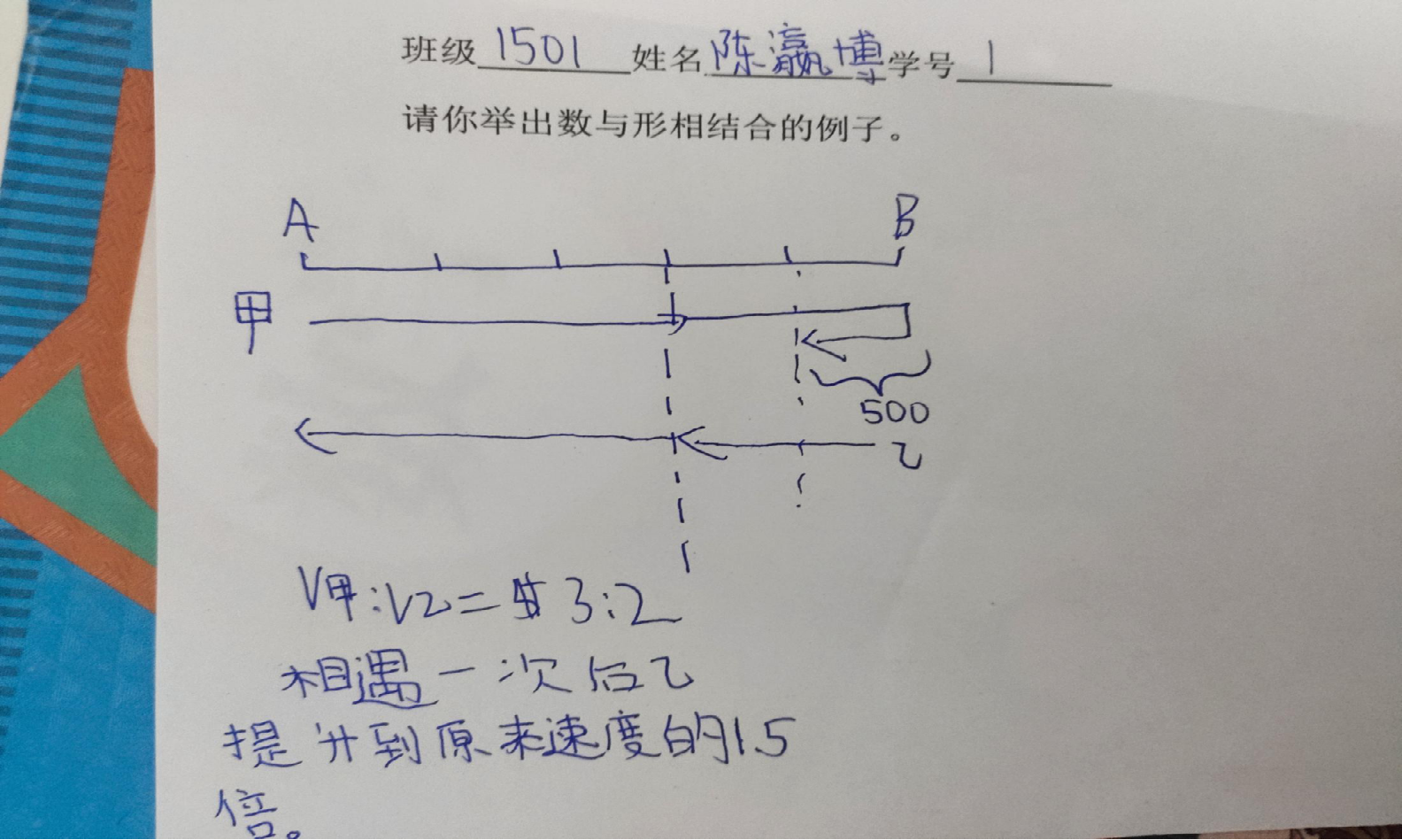
4、展示其他例子:
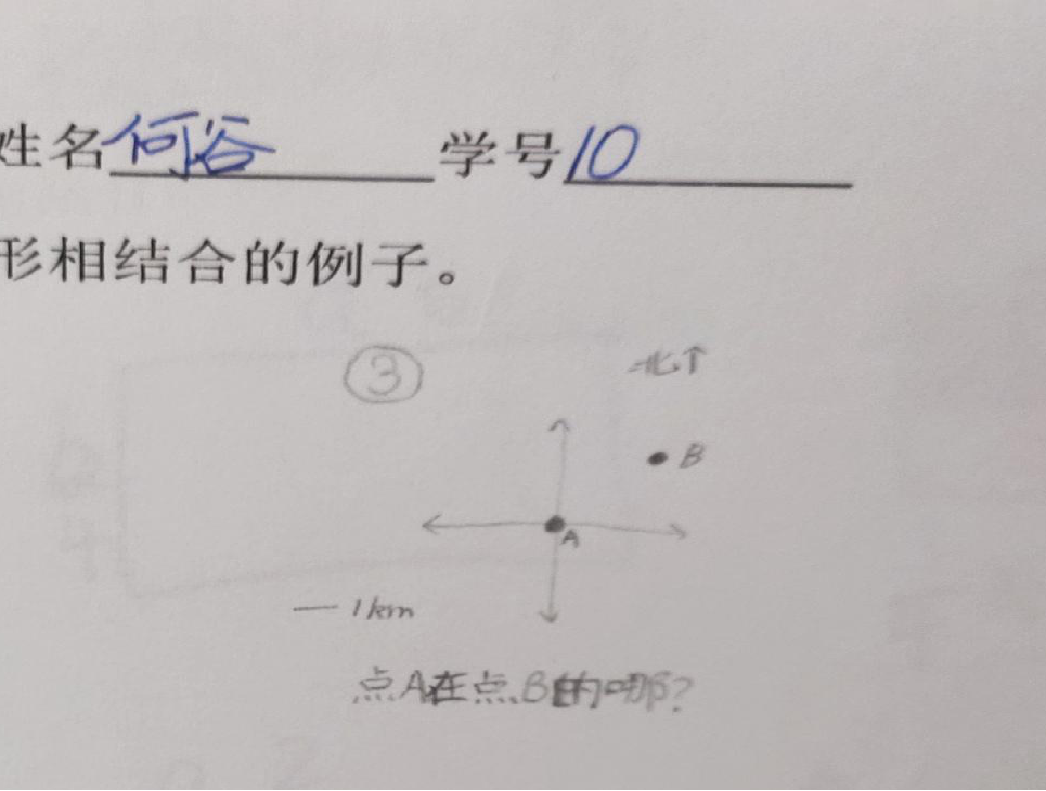
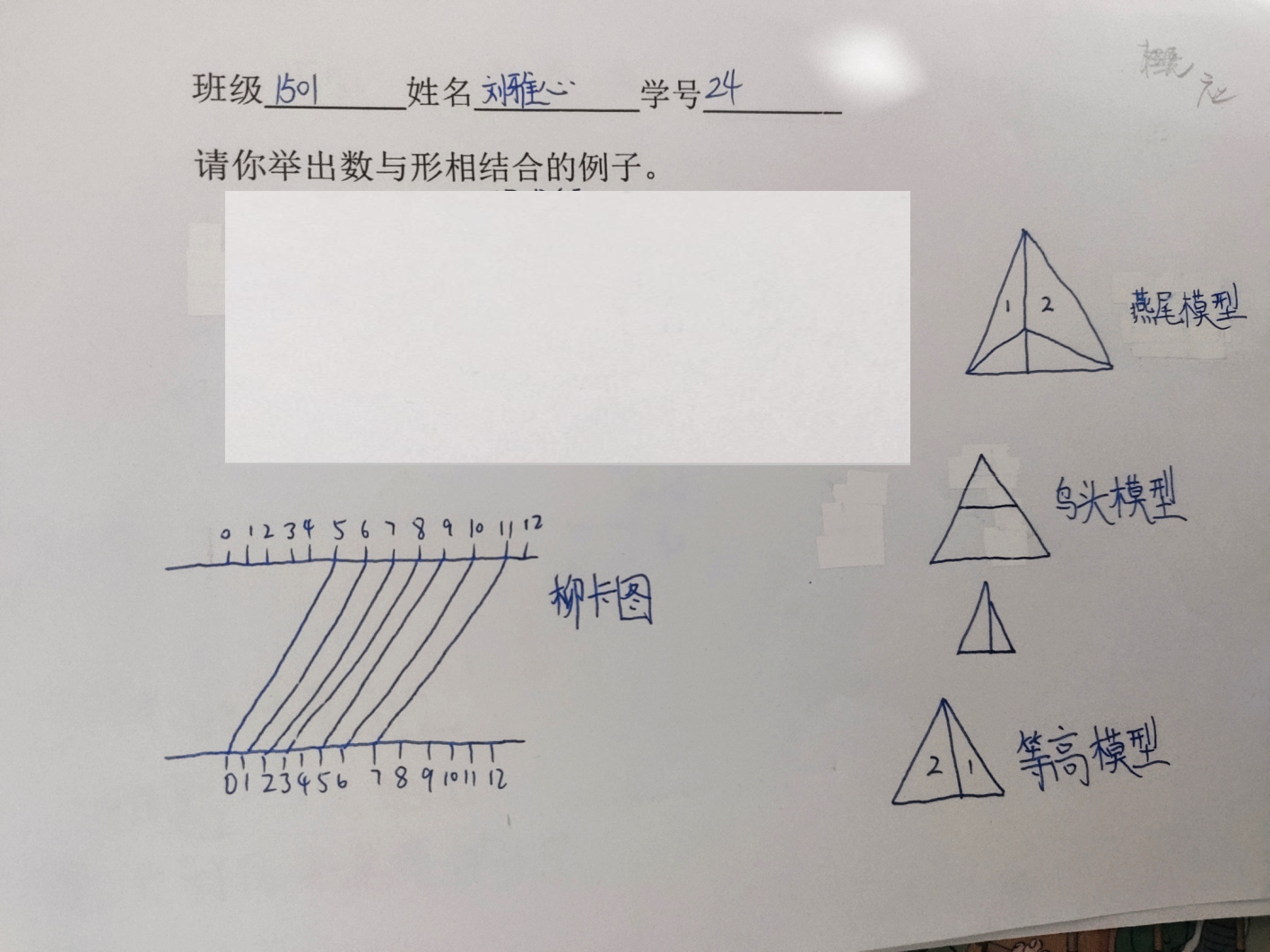

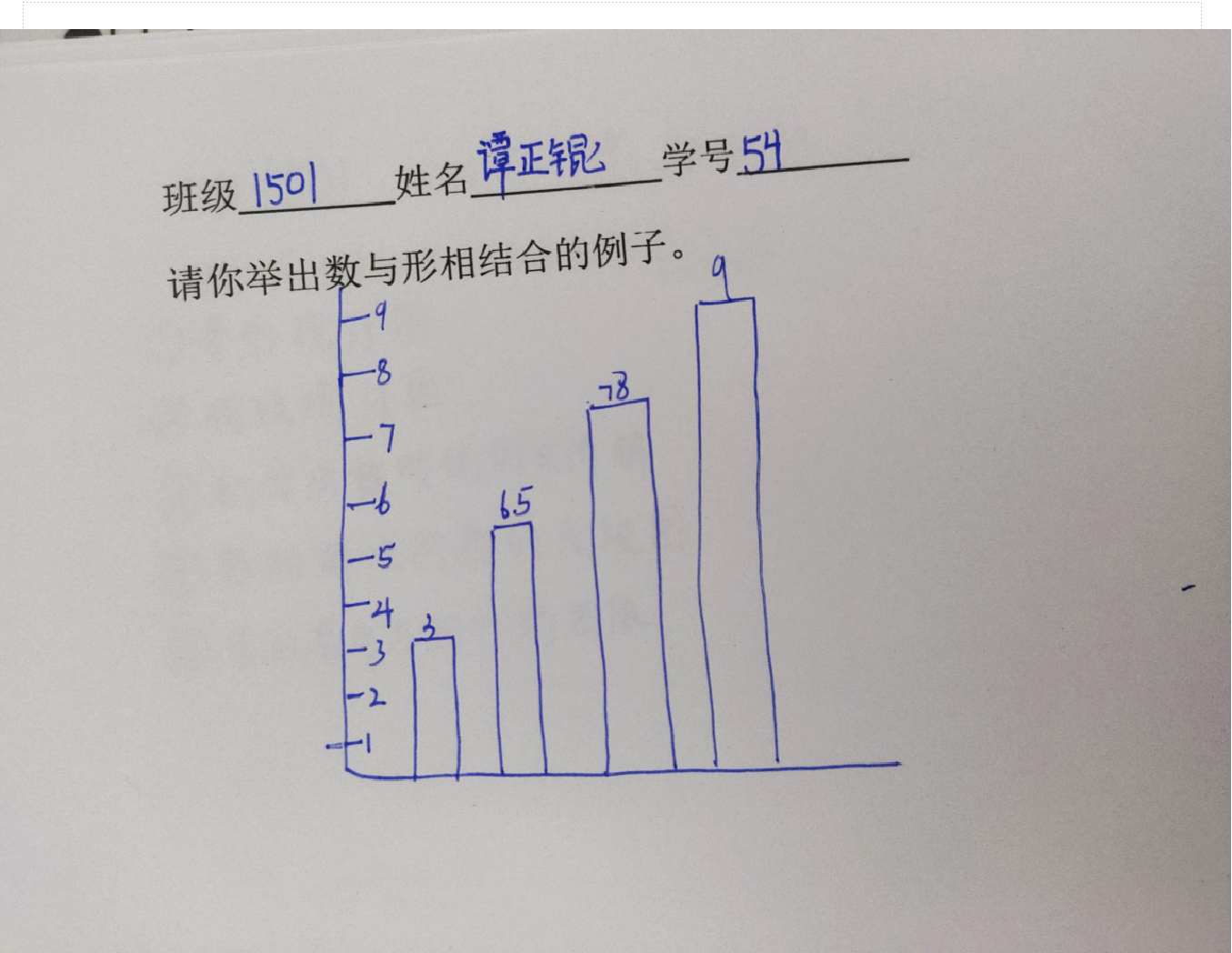


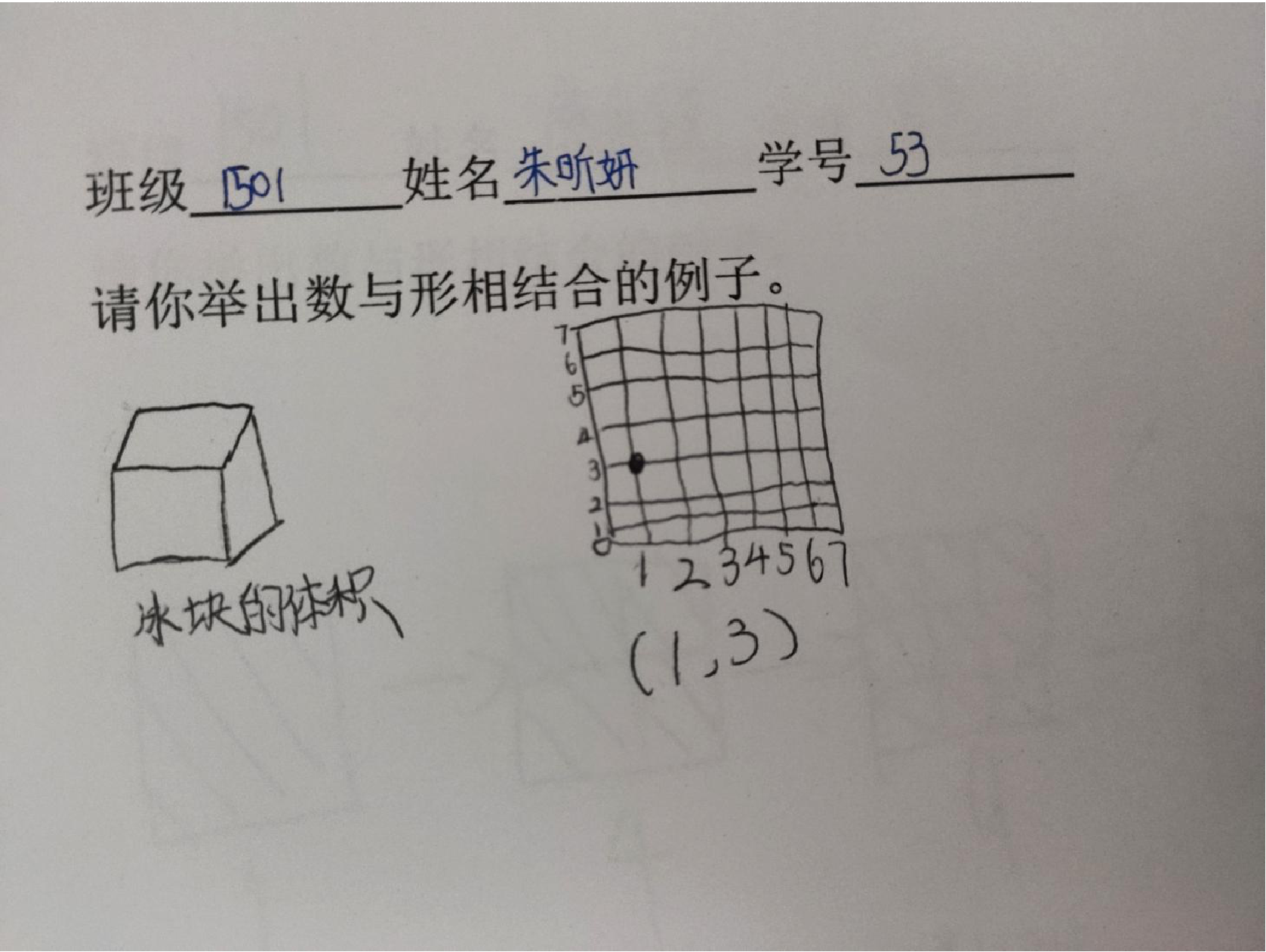
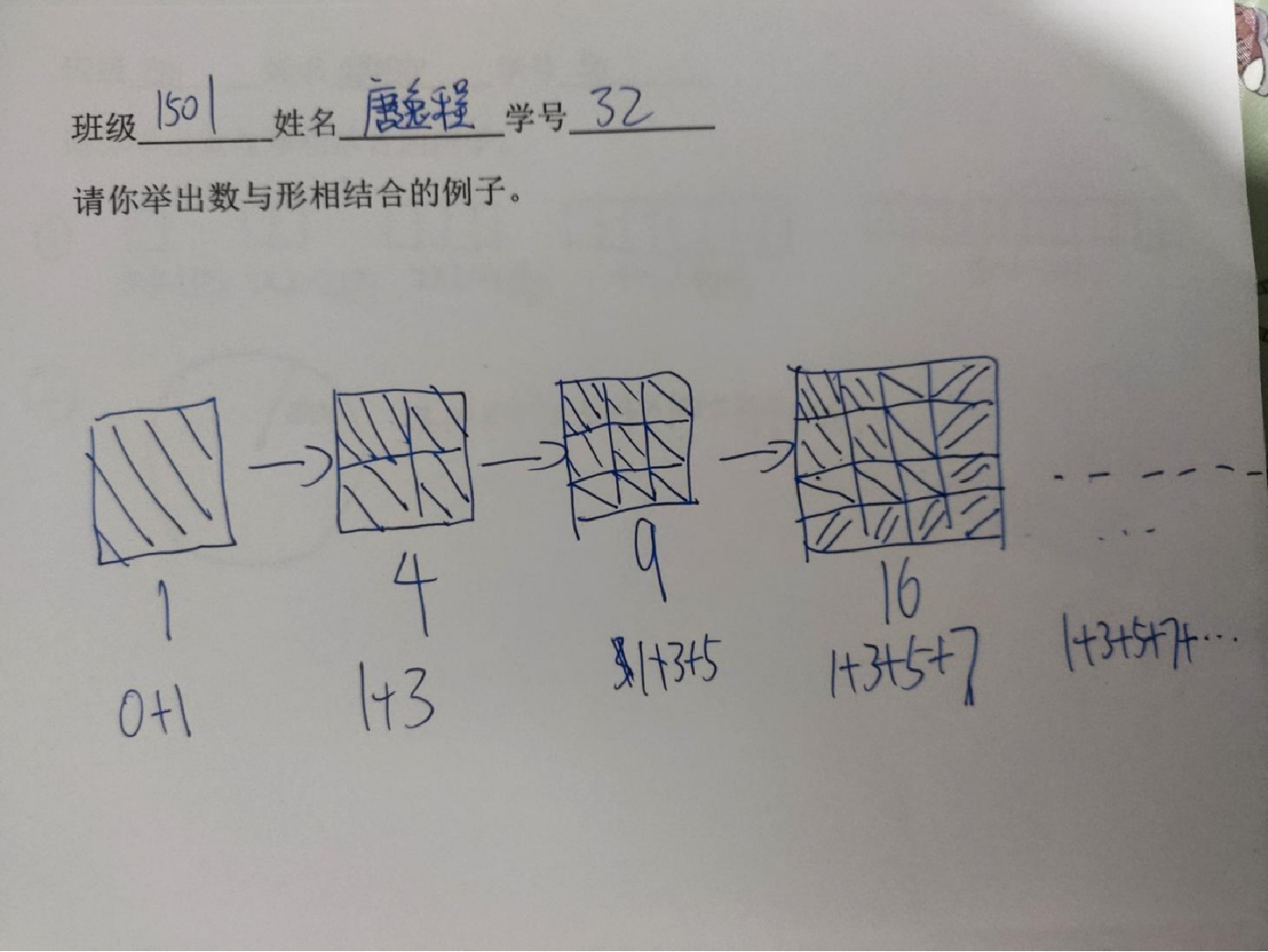
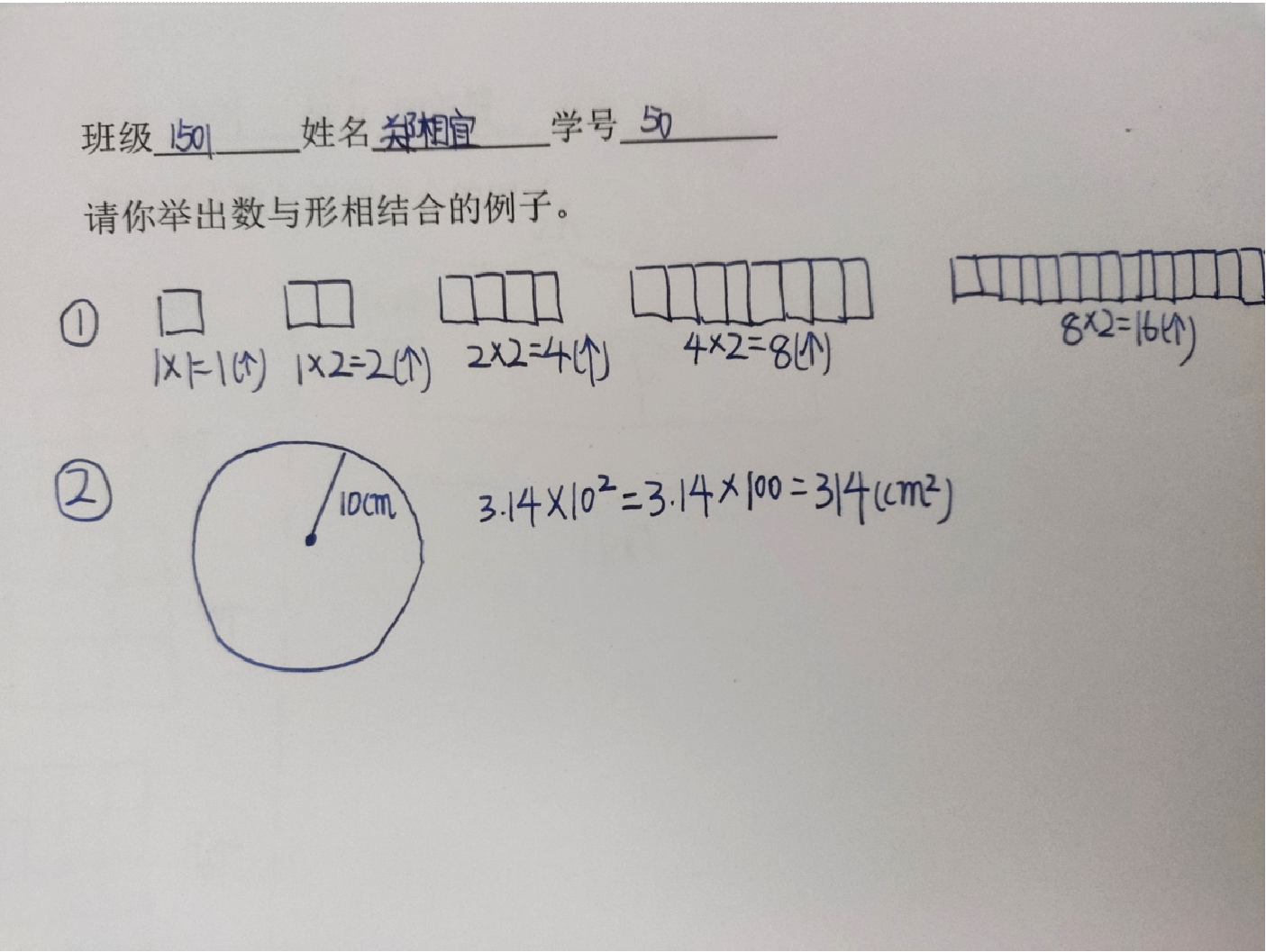

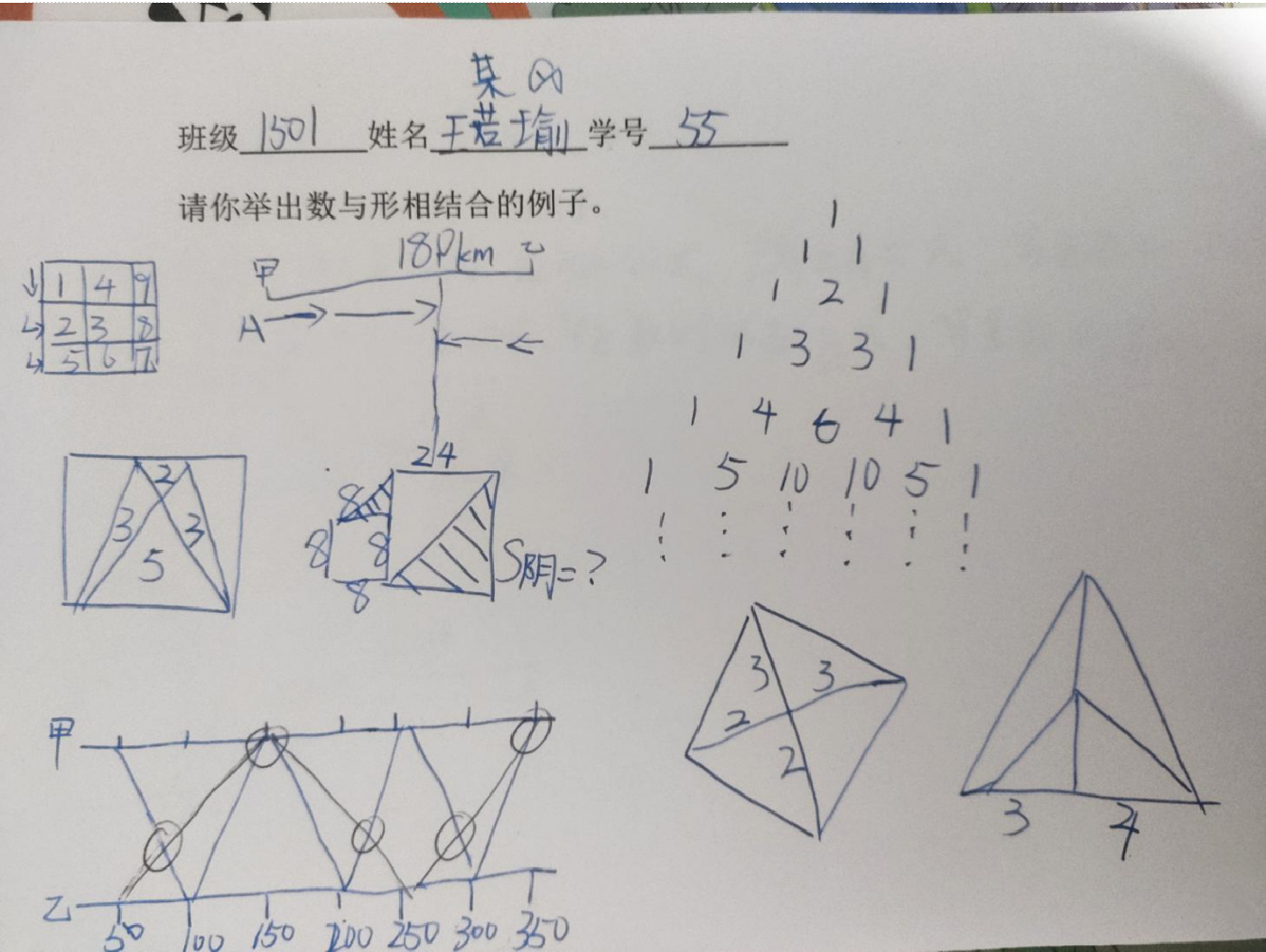
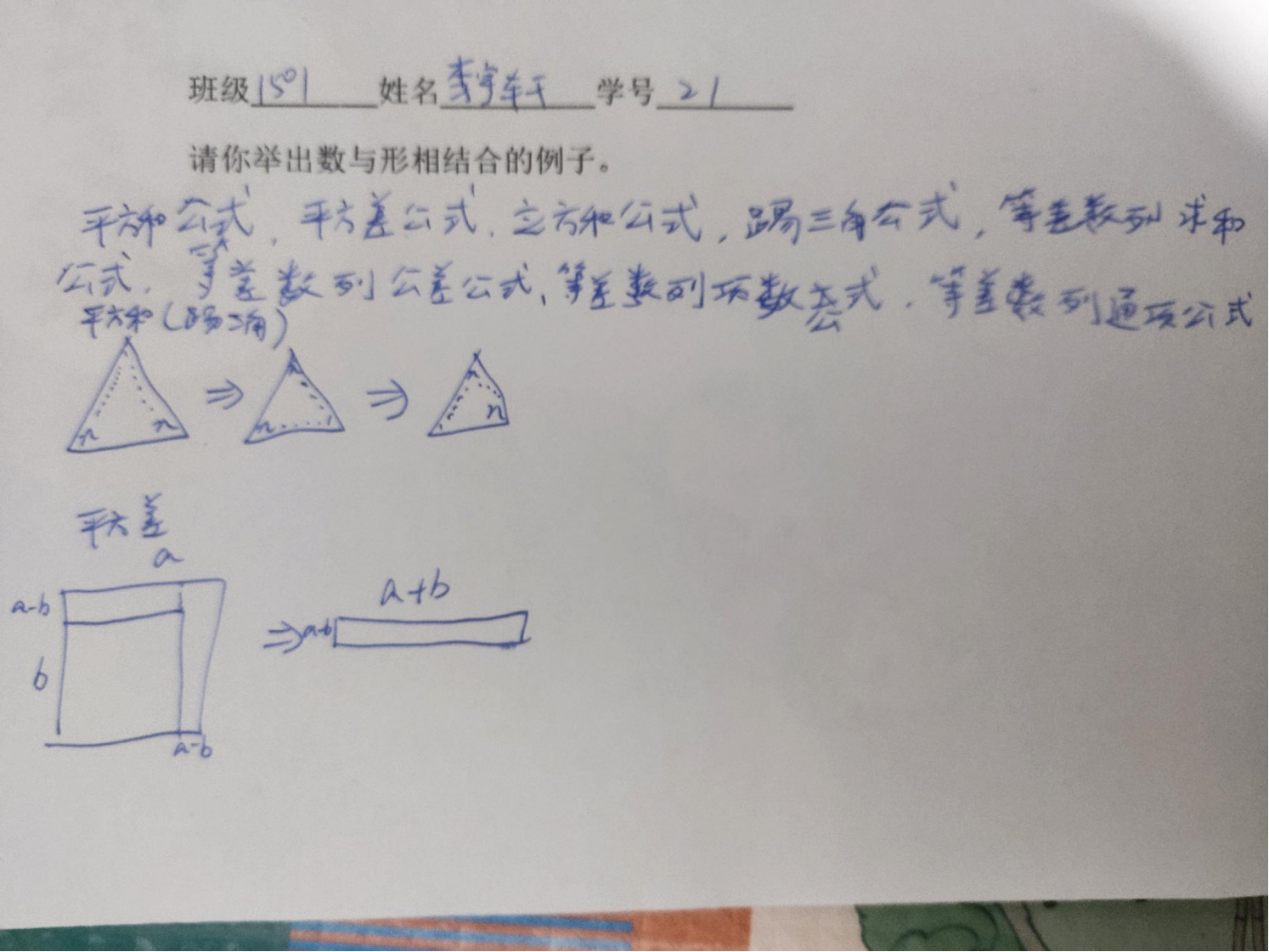

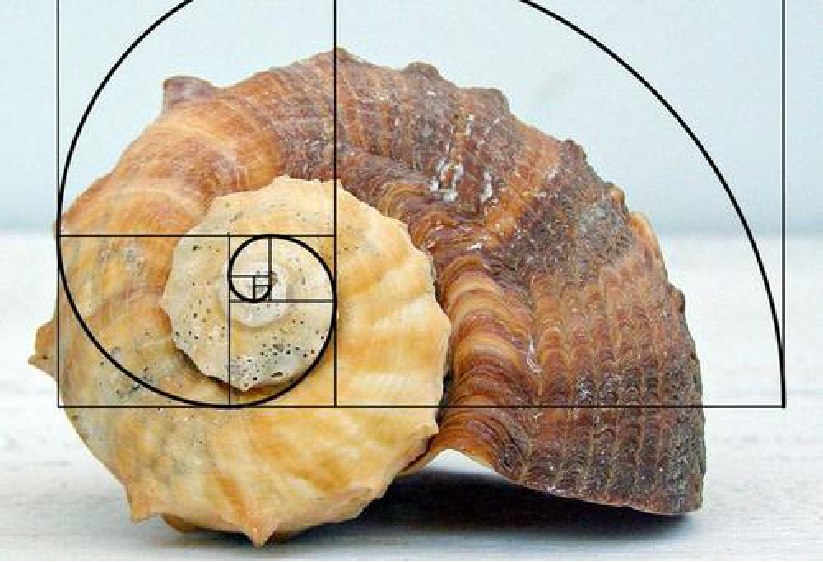
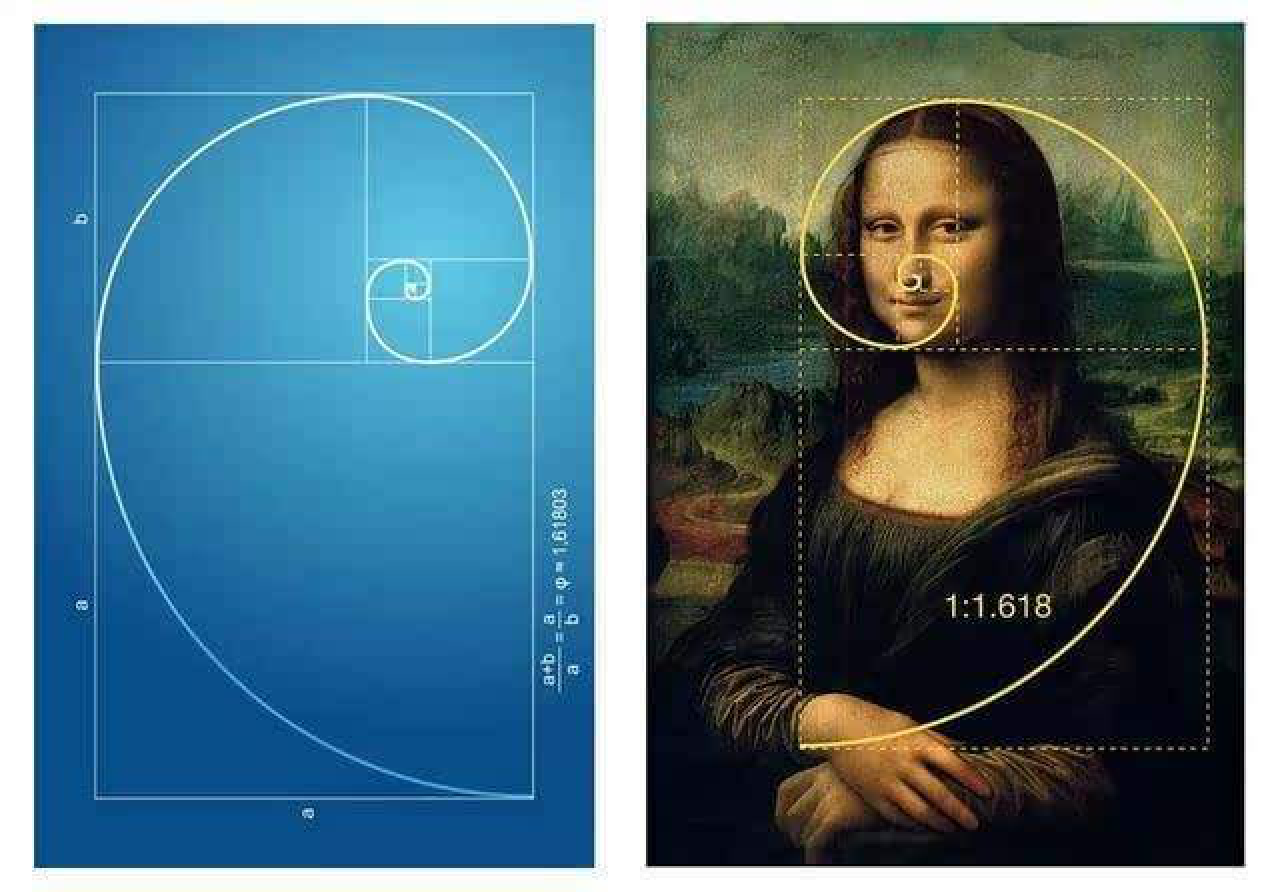
三、探究题
(1)

展示学生作品并请学生解释。
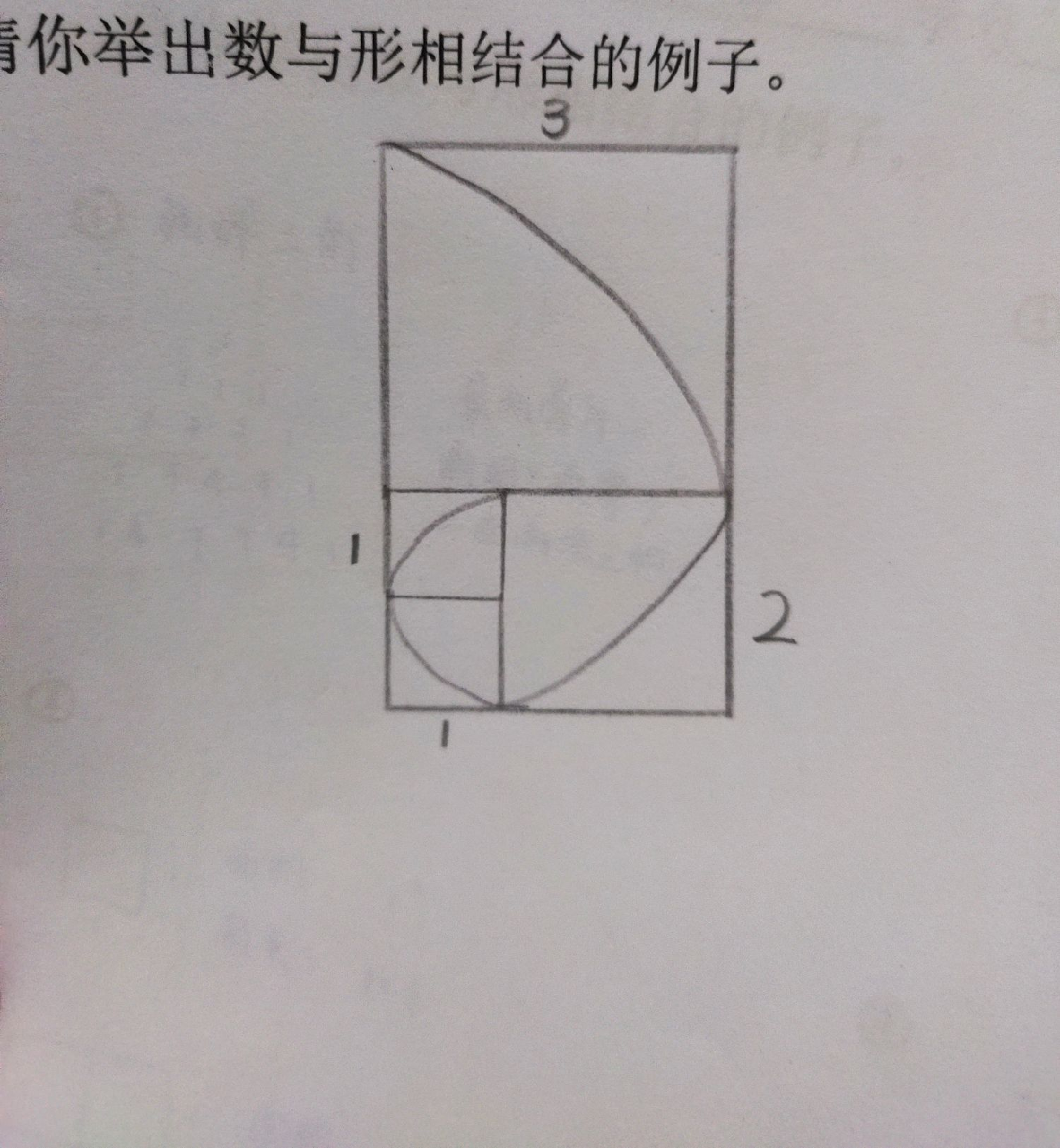
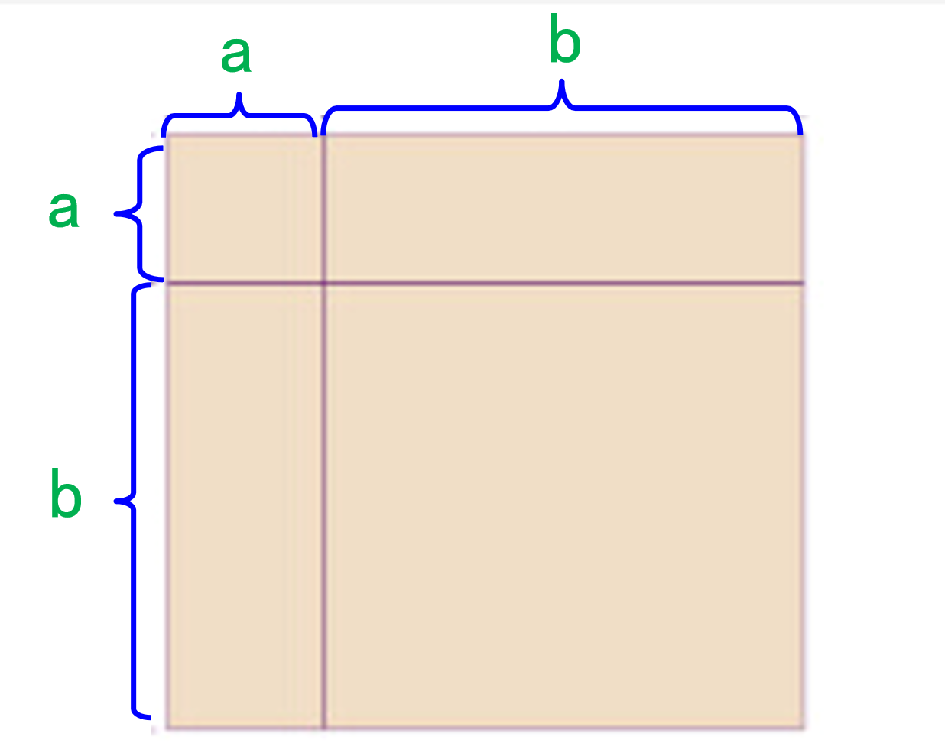
(2)请你想办法求出下面这个图形的面积。
四、勾股定理拓展:
见数思形,见形想数
9+16=25,所以边长为3的正方形面积加上边长为4的正方形面积等于边长为5的正方形面积。
动画演示。
播放验证勾股定理的2个视频。
五、同学们,通过今天的学习,你有什么收获?
设为正确答案