- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



《平面镶嵌》是人教版八年级上册第十一章《三角形》的数学活动课内容,是在介绍了三角形的概念及性质,多边形的内角和、外角和公式的基础上进行的,再次体现了多边形内角和公式在实际生活中的应用。教材从生活实例出发,引出平面镶嵌的概念,探究了三个问题:一是什么图形叫做正多边形;二是一种正多边形的镶嵌问题,通过动手实验、观察、分析,发现正三角形、正方形、正六边形能镶嵌;三是几种正多边形的镶嵌问题,探究正多边形平面镶嵌的原理。本课的学习,让学生经历从实际问题抽象出数学问题,建立数学模型,综合应用已有知识解决问题的过程,加深对相关知识的理解,提高思维能力。
八年级学生对镶嵌的认识大多数来源于生活实际中的感性认识,对镶嵌的内在规律关注不够,因而教师在教学本节时应通过创设情境、组织学生动手操作,让学生在活动中共同探究从而加深对镶嵌的认识,发现其内在规律,将感性认识上升为理性认识。
(一)了解平面镶嵌的定义;
(二)掌握正多边形平面镶嵌的条件;
(三)探究两种正多边形平面镶嵌的条件,并利用方程思想解决这类问题。
(四)通过平面镶嵌活动,培养学生的创新精神和运用数学知识解决实际问题的能力。
教学重点:
1、掌握正多边形平面镶嵌的条件;
2、探究一种正多边形、两种正多边形的镶嵌问题。
教学难点:探究如何用方程思想解决两种正多边形平面镶嵌
用小视频的形式展示埃舍尔的平面镶嵌艺术作品《黑白鸟的镶嵌》《骑士平面镶嵌》、蜂巢、水立方等从古至今,在建筑设计中平面镶嵌的艺术作品。

同学们通过观察上述图片,你能发现它们具有什么样的特征吗?
下面两个图形是和上面图形一样吗?有什么区别?假如你们家地板铺成这样你会满意吗?
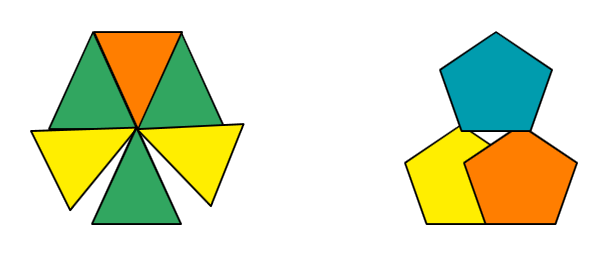
平面镶嵌定义:
从一个顶点出发,用形状大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠铺成一片,就是平面镶嵌。
找出平面镶嵌定义中的关键词:
①由形状、大小完全相同的图形拼接而成 ②无缝隙、③无重叠、④从一个顶点出发
究竟有哪些图形可以进行平面镶嵌呢?
探究活动一:同种正多边形的镶嵌
张老师家需要一个设计团队帮忙设计地砖,展示某建材市场选购的地砖,分别有正三角形、正方形、正方形、正五边形、正六边形的地砖,如果只选择一种进行地面装饰,哪几种砖可以选择呢?
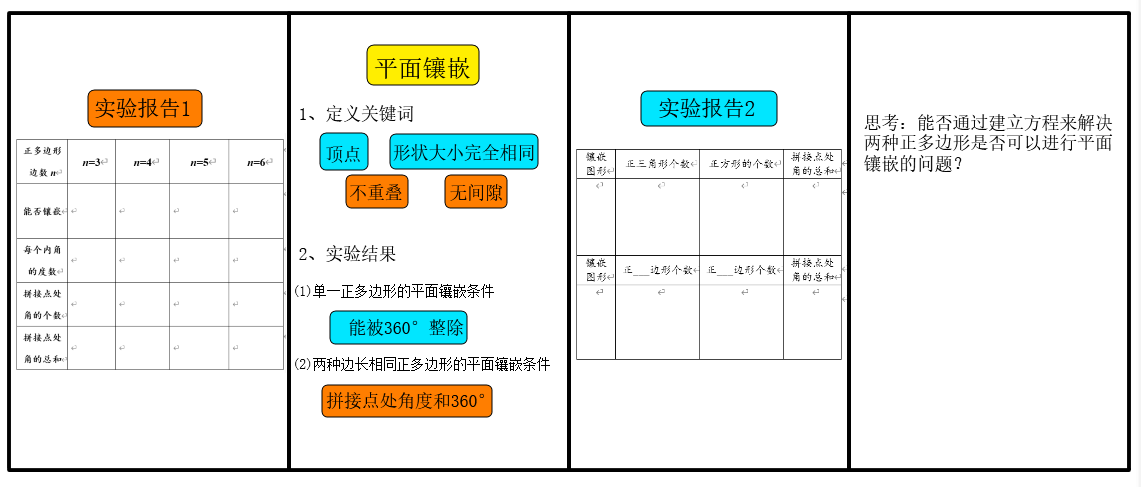
实验报告一
实验课题:单一正多边形的镶嵌
实验目的:探究用一种正多边形镶嵌的条件
实验材料:正三角形、正方形、正五边形、正六边形
实验步骤与观察记录:
| 正多边形边数 | n=3 | n=4 | n=5 | n=6 |
| 能否镶嵌 | ||||
| 每个内角的度数 | ||||
| 拼接点处角的个数 | ||||
| 拼接点处角的总和 |
实验结果:
(1)能单独进行平面镶嵌的是什么?
(2)用一种正多边形镶嵌,则拼接点处应满足的条件是什么?
该正多边形的内角应满足什么条件?
趁热打铁:
1、由三个完全相同的正多边形拼成的无缝不重叠的一部分,这种正多边形是:
A、正三角形 B、正方形 C、正六边形 D、正八边形
2、若铺满地的瓷砖每一个顶点处由6块相同的正多边形组成,则该正多边形的每一个内角度数为:
A、120°; B、90°; C、60°; D、45°;
探究活动二:边长相等的两种正多边形的组合镶嵌
张老师觉得一种图形的地板过于单一,想用边长相等的正三角形和正方形两种地板进行组合,各位设计团队你们能找到哪些组合方案呢?你还能从正三角形、正方形、正五边形、正六边形中选两个地板进行组合镶嵌吗?小组PK,看哪个小组地板最好看。
实验报告二
实验课题:用两种正多边形进行组合镶嵌
实验目的:探究用两种正多边形组合镶嵌需要满足的条件
实验材料:边长相等的正三角形、正方形、正五边形、正六边形
实验步骤与观察记录:
| 镶嵌图形 | 正三角形个数 | 正方形个数 | 拼接点处角的总和 |
| 镶嵌图形 | 正 边形个数 | 正 边形个数 | 拼接点处角的总和 |
实验结果:(1)从边长相等的正三角形、正方形、正五边形和正六边形中任选两种图形组合,能够进行镶嵌的是:
(2)思考1:能否通过建立方程来解决两种图形是否可以进行平面镶嵌的问题?
思考2:为什么要求用边长相等的两种正多边形,如果正多边形不相等,能否进行平面镶嵌?
(3)能够进行平面镶嵌的条件是什么?
①拼接点处几个角的和是多少?
②相拼接的边有什么特点?
趁热打铁:
3、下列能进行平面镶嵌的有
①正五边形和正方形;
②正五边形和正六边形
思维拓展:正五边形和正六边形
探究活动三:任意多边形的镶嵌
装修师傅在装修过程中用一些边角余料切割成一些形状、大小完全相同的任意三角形,他能用这些三角形进行地面镶嵌吗?任意四边形呢?
请同学们利用手中任意三角形、四边形模具动手操作,并完成探究报告3。
实验报告3
| 拼图 | 拼接点处角的个数 | 拼接点处角与多边形内角的关系 | 能否镶嵌 | |
| 任意三角形 | ||||
| 任意四边形 |
1、今天我们学习了哪些内容?
2、单一正多边形平面镶嵌需要满足什么条件?
3、两种正多边形组合镶嵌需要满足什么条件?用到哪一个数学思想方法?
装修师傅在装修过程中用一些边角余料切割成一些形状、大小完全相同的任意三角形,他能用这些三角形进行地面镶嵌吗?任意四边形呢?
请同学们课后利用手中任意三角形、四边形模具动手操作,并完成实验报告3。
实验报告3
实验课题:任意多边形的平面镶嵌
实验目的:探究用完全相同的任意三角形或者任意四边形能否单独镶嵌。
实验材料:卡纸,剪刀。
实验步骤与观察记录:
| 任意三角形 | 任意四边形 | |
| 拼图 | ||
| 拼接点处角的个数 | ||
| 拼接点处角与多边形内角的关系 | ||
| 能否镶嵌 |
实验结果:
(1)单独用完全相同的三角形 进行平面镶嵌;单独用完全相同的四边形 进行平面镶嵌。(填“能”或“不能”)
(2)单独用一种多边形能够进行平面镶嵌的条件是什么?
设为正确答案