- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课在已学指数函数的概念,接着研究指数函数的图像和性质,从而深化学生对指数函数的理解,并且了解较为全面的研究函数的方法,为以后在研究对数函数函数打下基础.教材强调数形结合思想方法的运用,利用指数函数的图象探究指数函数的性质,并用所得到的性质进一步理解指数函数的图象.教材充分关注了与实际问题的练习,体现数学应用的价值.另外,本节内容具有数形结合的特点,充分发挥信息技术的作用,尽量利用信息技术创设教学情境,为学生的数学探究和数学思维提供支持,更好地克服可能遇到的困难,理解指数函数的概念、图象和性质.
学生已学习了幂函数的图象和性质,已经了解将函数图象作为研究函数性质的直观工具,学生在此过程中积累了利用函数图象研究函数性质的经验.在此基础上,指数函数的图象和性质的教学应该以学生为主,引导学生类比研究幂函数的图象和性质的过程和方法.
课程目标:
1、掌握指数函数的图象和性质,培养学生实际应用函数性质的能力;
2、通过观察图象,分析、归纳、总结指数函数的性质;
3、在指数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
数学学科素养:
1.数学抽象:借助指数函数的图象研究函数的性质;
2.逻辑推理:由指数函数的图象推出指数函数
的图象;
3.直观想象:指数函数的图象;
4.数学运算:求函数的定义域、值域与指数函数的值;
5.数据分析:利用指数函数的性质比较两个函数值的大小:
6.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
重点:指数函数的图象和性质;
难点:对底数的分类,如何由图象、解析式归纳指数函数的性质以及性质的理解.
4.2.2指数函数的图像与性质
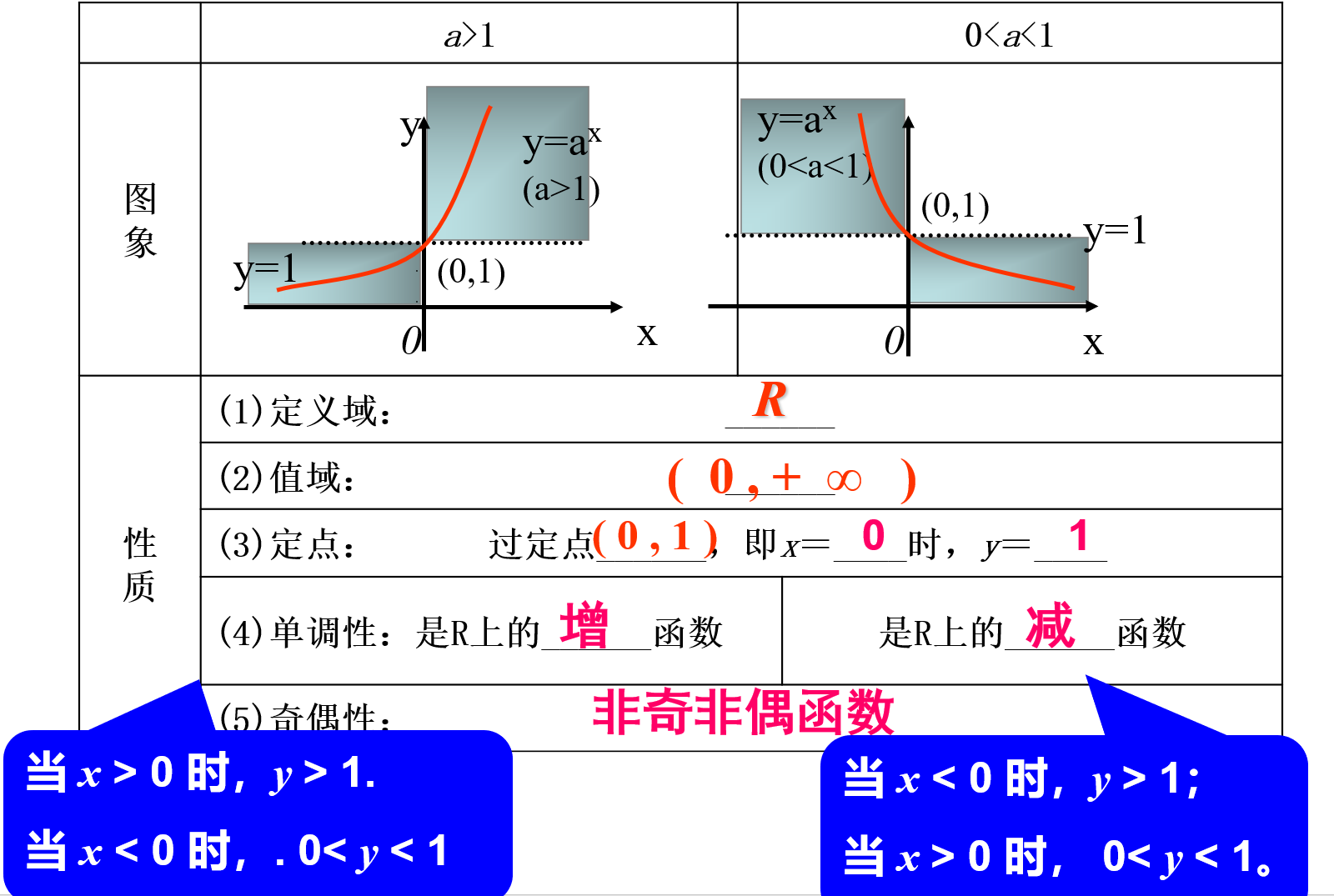
1.指数函数图像
2. 指数函数的性质 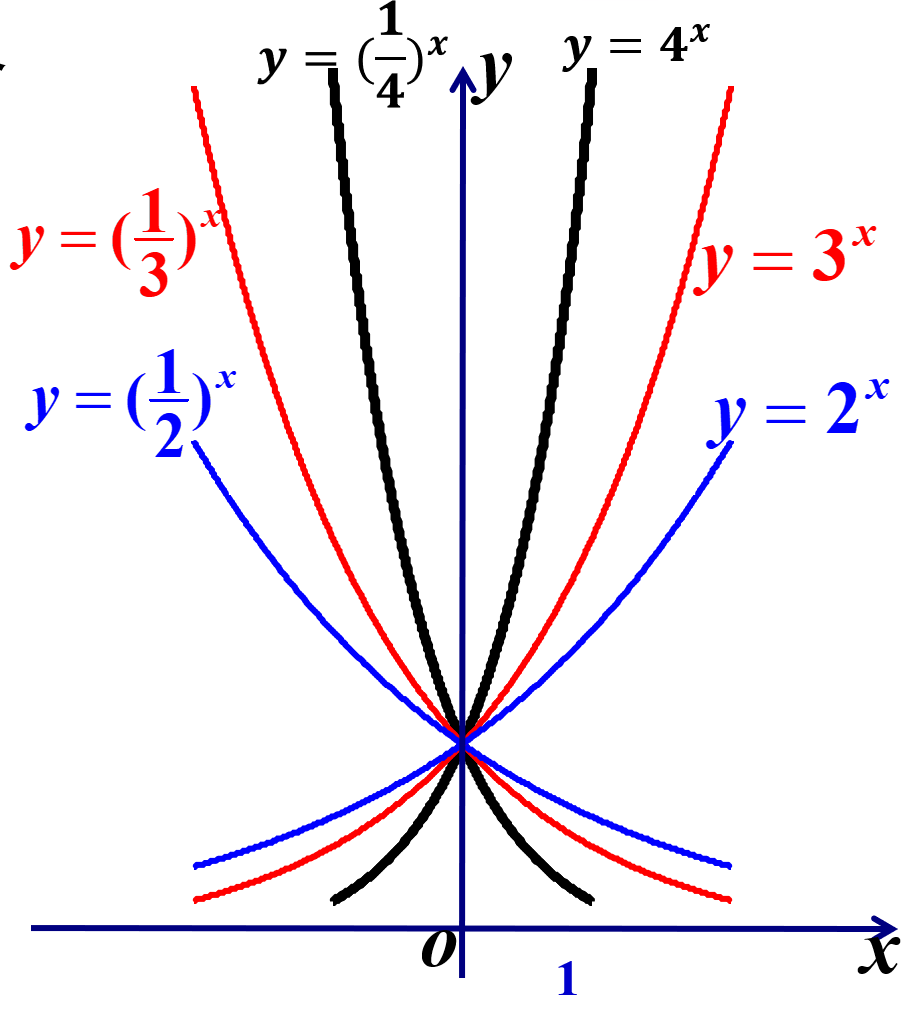
3.例题
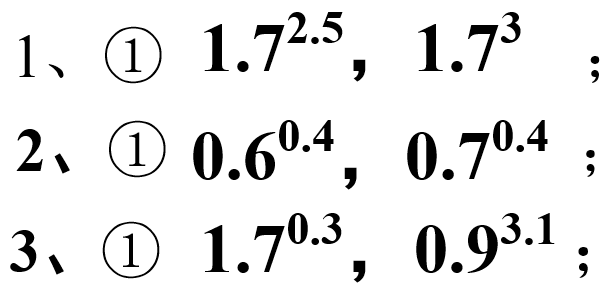
总结:
1、底数相同,指数不同型
2、底数不同,指数相同型
3、底数不同,指数不同型
4.小结
请学生判断和
是什么类型的函数,从而复习上节课指数函数的概念,接着让学生比较
与1的大小关系.再以问题“你能说说研究函数性质的一般步骤和方法吗?”引发学生思考.
要求:让学生自由发言,教师不做判断。而是引导学生进一步研讨.
阅读课本116-117页,思考并完成以下问题
1. 结合指数函数的图象,可归纳出指数函数具有哪些性质?
2. 指数函数的图象过哪个定点?如何求指数型函数的定义域和值域问题?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
1、请学生在黑板上画出指数函数和
的图象

探究:和
的图象有什么关系?能否利用函数
的图象,画出函数
的图象?
与
的图象关于y轴对称,教师和学生一起证明.
2、和学生一起总结出指数函数的性质
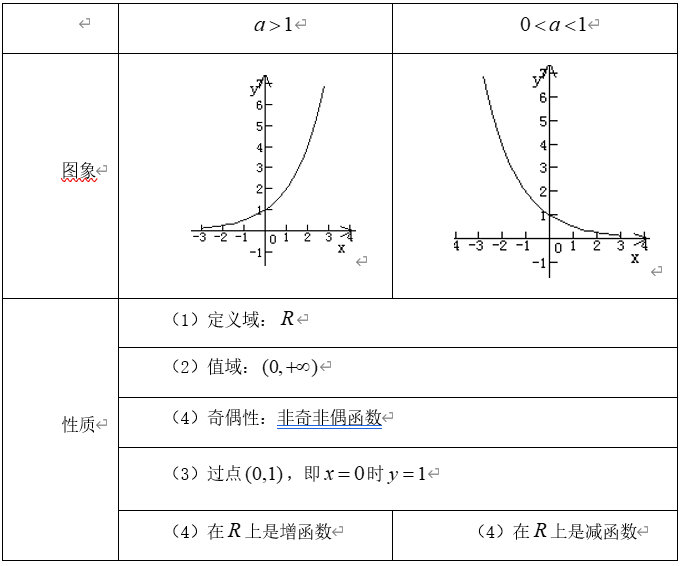
3.引导学生思考指数函数图象有什么变化规律
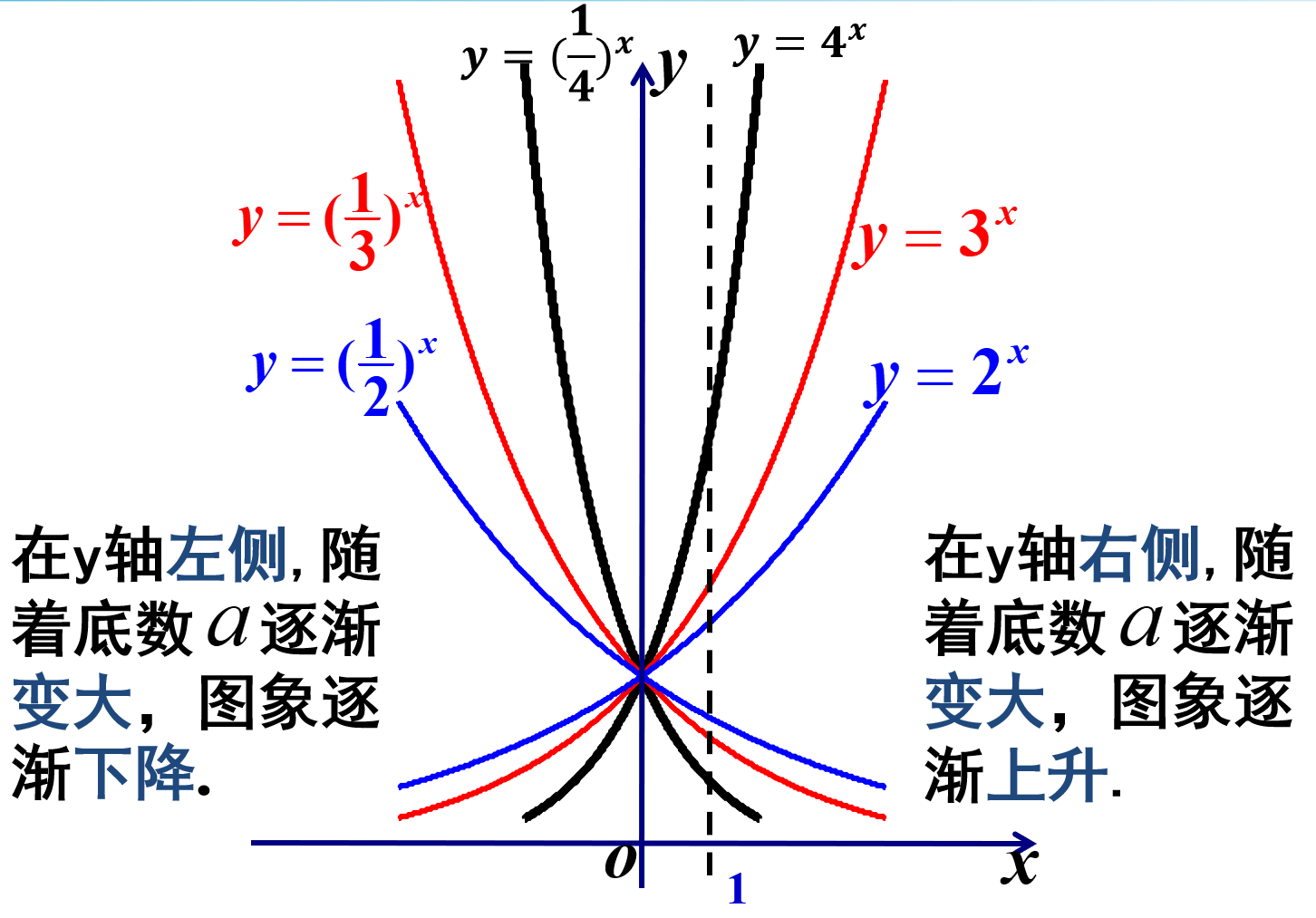
题型一 指数函数的性质比较大小




题点二:指数型函数图象的变化规律的应用

题点三:

练习: 函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )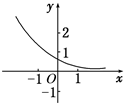
A.a>1,b<0 B.a>1,b>0
C.0<a<1,b>0 D. 0<a<1,b<0
【答案】D
【解析】从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0<a<1;从曲线位置看,是由函数y=ax(0<a<1)的图象向左平移|-b|个单位长度得到,所以-b>0,即b<0.
解题技巧:(指数函数的图像问题)
1.指数函数在同一平面直角坐标系中的图象的相对位置与底数大小的关系:在y轴右侧,图象从上到下相应的底数由大变小;在y轴左侧,图象从上到下相应的底数由小变大.
无论指数函数的底数a如何变化,指数函数y=ax(a>0,且a≠1)的图象与直线x=1相交于点(1,a),因此,直线x=1与各图象交点的纵坐标即为底数,由此可得底数的大小.
2.指数函数与y=
(a>0,且a≠1)的图象关于y轴对称.
3.处理函数图象问题的常用方法:一是抓住图象上的特殊点;二是利用图象的变换;三是利用函数的奇偶性与单调性.
让学生总结本节课所学主要知识及解题技巧
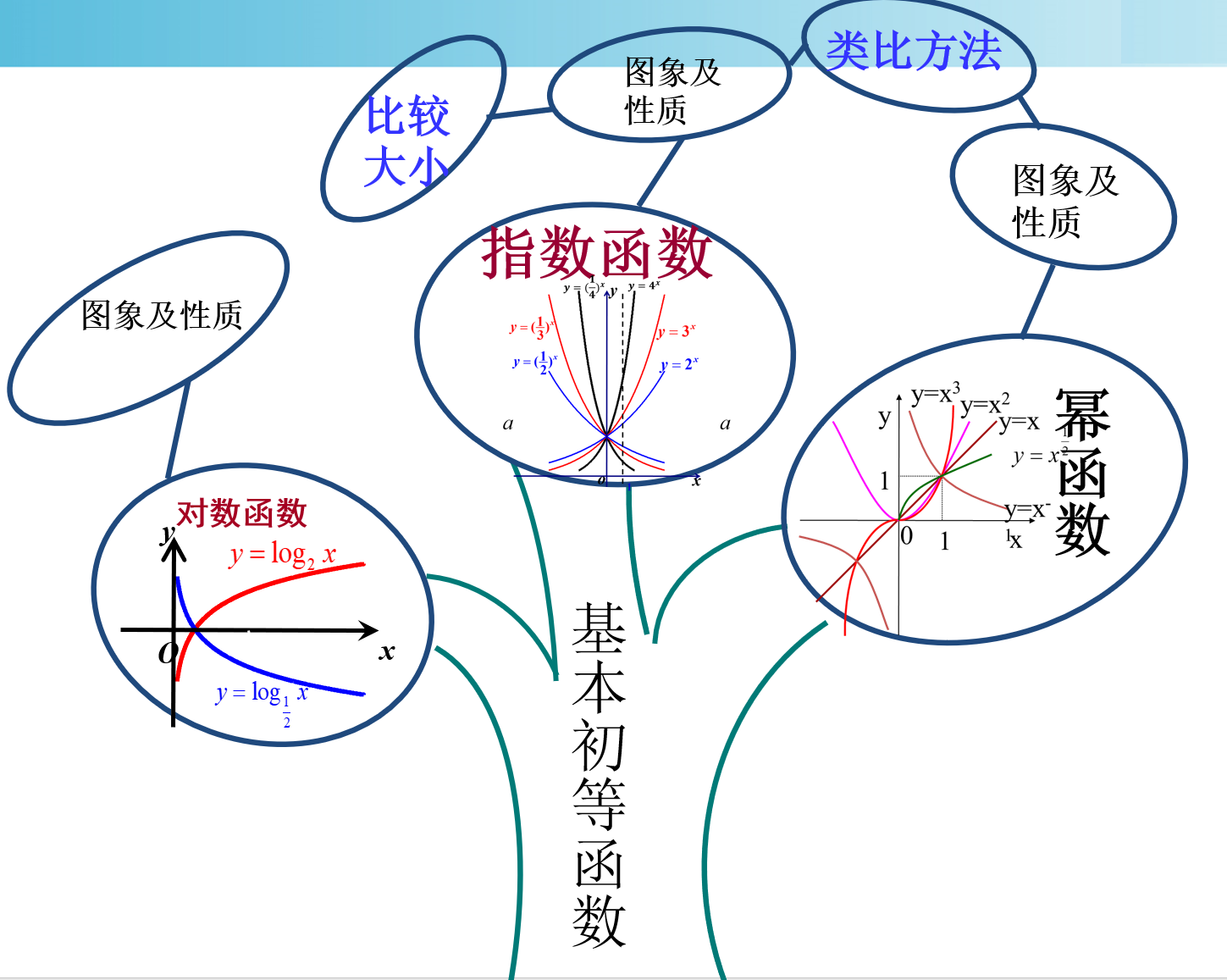
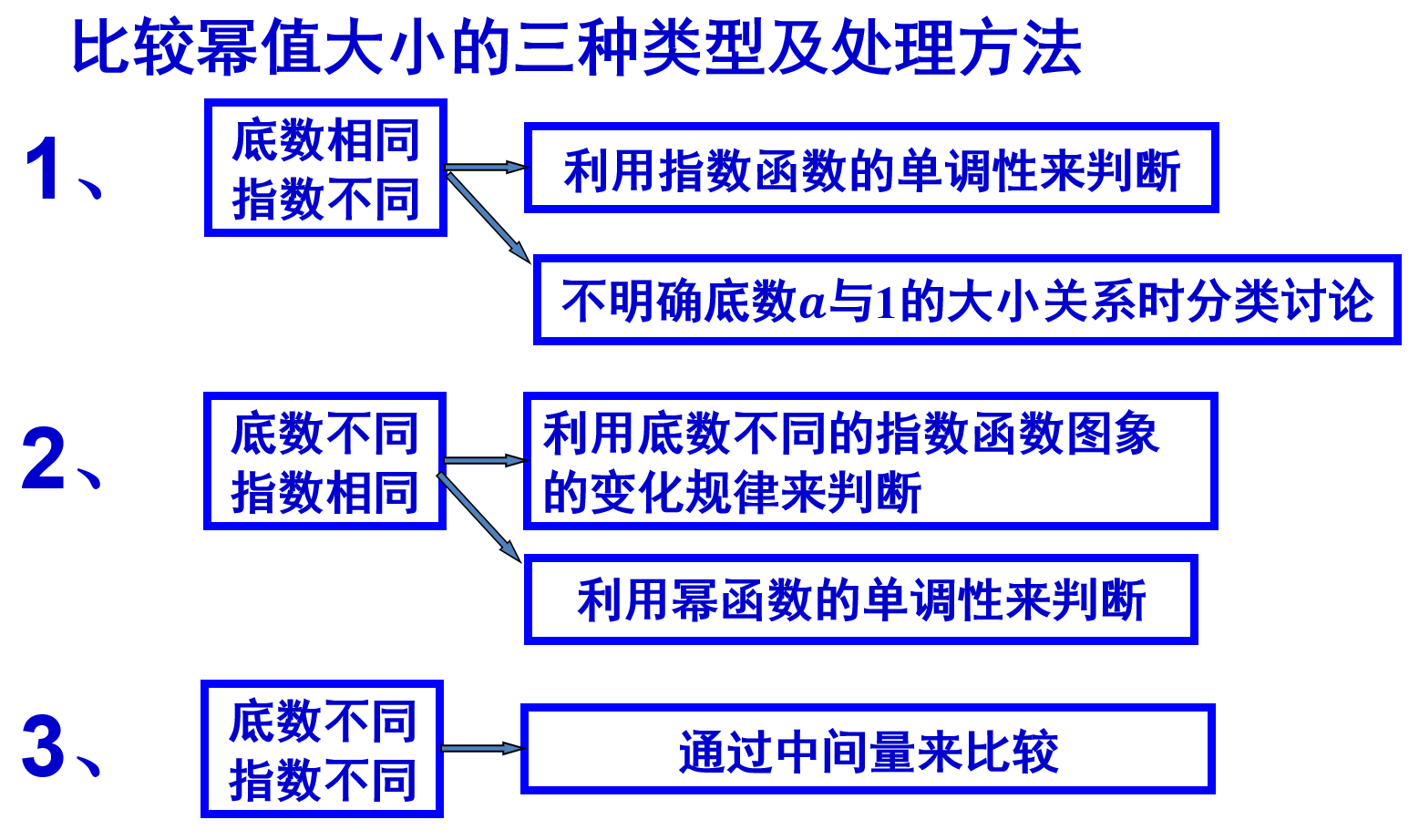
课本118页习题4.2
跟踪训练一
1、如图是指数数:①y=ax,②y=bx,③y=cx,④y=dx的图象,则a,b,c,d与1的大小关系是( )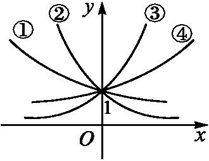
A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
2、已知函数f(x)=ax+1+3的图象一定过点P,则点P的坐标是 .
【答案】1. B 2. (-1,4)
【解析】1、解析:(方法一)①②中函数的底数小于1且大于0,在y轴右边,底数越小,图象
向下越靠近x轴,故有b<a,③④中函数的底数大于1,在y轴右边,底数越大,
图象向上越靠近y轴,故有d<c.故选B.
(方法二)作直线x=1,与函数①,②,③,④的图象分别交于A,B,C,D四点,
将x=1代入各个函数可得函数值等于底数值,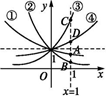
所以交点的纵坐标越大,则对应函数的底数越大.
由图可知b<a<1<d<c.故选B.
答案:B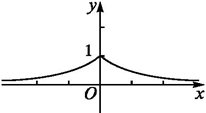
2、解析:∵当x+1=0,即x=-1时,f(x)=a0+3=4恒成立,故函数f(x)=ax+1+3恒过(-1,4)点.
3. 比较下列各题中两个值的大小:

【答案】(1) 1.72.5<1.73 (2) (3)1.70.3 > 0.93.1
【解析】(1)(单调性法)由于的底数是1.7,故构造函数y=1.7x,而函数y=1.7x在R上是
增函数.又2.5<3,∴1.72.5<1.73
(2)(单调性法)由于的底数是0.8,故构造函数y=0.8x,而函数y=0.8x在R上是减函数.又
,所以
(3)(中间量法)由指数函数的性质,知0.93.1<0.90=1,1.70.3>1.70=1,则1.70.3 > 0.93.1
跟踪训练二
1、比较下面两个数的大小:
(a-1)1.3与(a-1)2.4(a>1,且a≠2).
2、比较下列各题中两个值的大小:
①2.53,2.55.7;
②1.5-7,;
③2.3-0.28,0.67-3.1.
【答案】1.当a>2时,(a-1)1.3<(a-1)2.4;当1<a<2时,(a-1)1.3>(a-1)2.4.
2.① 2.53<2.55.7. .②1.5-7>. ③ 2.3-0.28<0.67-3.1.
【解析】1、因为a>1,且a≠2,所以a-1>0,且a-1≠1,
若a-1>1,即a>2,则y=(a-1)x是增函数,∴(a-1)1.3<(a-1)2.4.
若0<a-1<1,即1<a<2,则y=(a-1)x是减函数,∴(a-1)1.3>(a-1)2.4.
故当a>2时,(a-1)1.3<(a-1)2.4;
当1<a<2时,(a-1)1.3>(a-1)2.4.
2.①(单调性法)由于2.53与2.55.7的底数是2.5,故构造函数y=2.5x,而函数y=2.5x在R上是增函数.
又3<5.7,∴2.53<2.55.7.
②(化同底)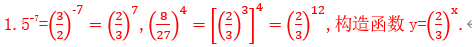
![]() 在R上是减函数.又7<12,
在R上是减函数.又7<12, .
.
③(中间量法)由指数函数的性质,知2.3-0.28<2.30=1,0.67-3.1>0.670=1,则2.3-0.28<0.67-3.1.
设为正确答案