- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



多边形的内角和这节课是人教版第五单元 例7四边形的内角和及扩展内容,在此之前已经学习了三角形、四边形、梯形等图形,还知道了三角形内角和是180度。探究三角形内角和主要用到了“转化”的数学思想方法,这节课要充分利用上述经验,利用“转化”的数学思想方法把四边形及其多边形转化为三角形来探究四边形及多边形的内角和。
四年级的学生在学了本节课之前,已经认识了三角形、四边形、平行四边形等基础图形,并已经有了学习三角形内角和的经验, 四年级学生对新知识具有一定的好奇心,同时也具备初步的数学探索与推理能力,能在原有知识的基础上利用之前学习的“转化”这一数学思想进行接下来的探索性学习。
知识与技能:掌握多边形内角和公式,能尝试运用多边形内角和公式求出多边形的内角和。
过程与方法:在探索中理解计算多边形内角和的思想方法,同时再次感知数学的转化思想。
情感态度与价值观:通过转化、归纳、总结一系列过程,培养学生的数学学习兴趣和探究精神。
重点:探究多边形内角和的公式。
难点:如何把多边形内角和转化为三角形内角和来推导。
多边形内角和
180度x( 边数-2)
1、复习三角形内角和
ppt出示三角形
师:前面我们学习了三角形,你知道三角形有哪些特征吗?三角形的内角和你记得是多少度吗?
生:三条边,三个顶点,三个角,内角和是180度
师:那你知道四边形的内角和会是多少度吗?
生:
师:今天我们就一起来探究四边形及其五边形,还有多边形的内角和
(师板书课题:多边形内角和)
1、探索四边形内角和
师:这是我们学习过的三角形,快看两个三角形可以拼成一个四边形
(ppt演示用三角形组成四边形)
师:两个三角形能组成一个四边形,那反过来一个四边形也就可以分成两个三角形,你同意吗?
生:不同意,,,,同意
师:有的同学同意,有的不同意,那我们试试看好不好?
学生活动:(在准备好的学习卡上进行分割)
师:那哪一位同学跟我们讲一讲你是怎么又快又准确的把四边形分成三角形的呢?
生1:可以从一个角的顶点出发向另一个对角画一条线就把这个四边形分成了两个三角形
师:总结:(引导学生)他这样从一个角的顶点出发连接未相连的顶点,这样就能把所有的四边形分成了两个三角形。
师:分三角形不是我们的目的呀,我们的目的是求内角和,那你觉得我们分三角形作用吗?
生:有,我们可以把四边形分成三角形来求内角和
师:哦,这位同学太有想法了,你可以给大家解释一下你的想法吗??
生:
师:给他掌声,这位同学提出了将四边形分割成两个三角形,进而将四边形的内角和问题转化为求两个三角形内角的和的问题,这样就把复杂的问题简单化了,真是了不起。
师:那你们能用这样的方式求出四边形的内角和吗?
生动手操作
师:那么谁来告诉老师你是怎么算出四边形内角和的呢?
生:
2、探究五边形、六边形的内角和
师:类似地,从一个顶点出发,你能将图形分成几个三角形呢?能通过这样的方法你能算出五边形、六边形…n边形的内角和是多少度吗?请小组合作完成,谁将是最聪明的小组呢?期待你们的表现!
(学生分组完成以下表格)
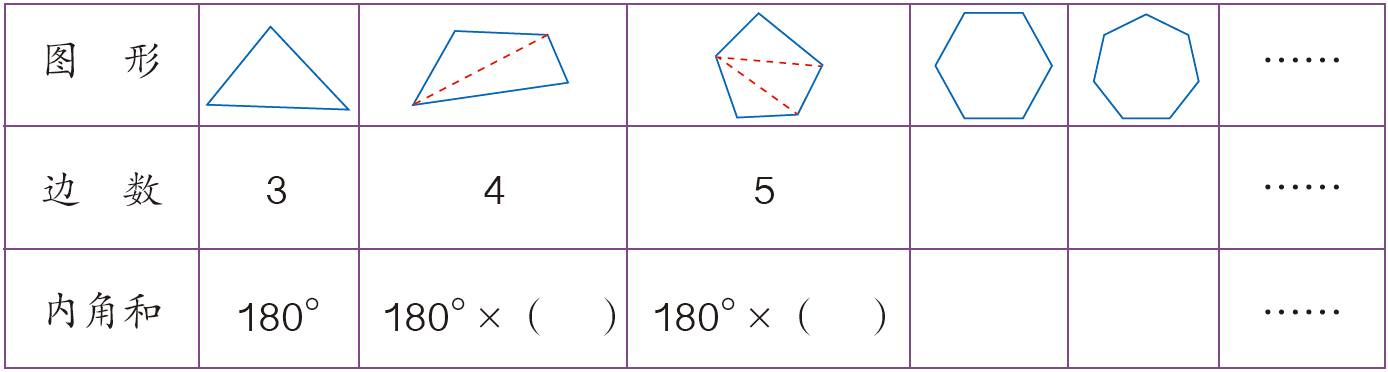
学生活动:学生分组讨论
然后代表汇报。
3.总结探索过程,发现规律,总结出n边形的公式
师:通过对四边形,五边形,六边形的研究,你有什么发现?你能知道七边形内角和是多少度吗?
生通过计算得出结果
师:你能发现多边形的边数跟分成三角形的数量有什么关系吗?
师生活动:学生独立思考后回答
最后总结出n边形的内角和等于边数-2再乘以180°
1、出示ppt:求出8边形的内角和是多少度?
师:看看谁最厉害快速的求出8边形的内角和
生尝试然后回答
2、快速说出多边形能分成几个三角形
3、两位同学pk
师:非常不错,这个难度不大,那我们比一比看谁更厉害些。哪两位同学来比一比?
生比试
师:在这节课中你学会了什么?
设为正确答案