- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课知识处在八年级上册第二章节后面的IT教室,主要以“轴对称知识”、“两点之间,线段最短”、“三角形三边关系”等为基础,借助计算机软件几何画板,来解决数学史上的一个经典问题——“将军饮马问题”。在教材中设置IT教室,目的在于让学生利用先进的信息技术解决数学问题,既能培养学生的兴趣,也能为学生研究数学提供新的方法,让学生知道数学应用强大,研究的方式多种多样,拓展思维。教材中学生经历将实际问题抽象为数学中的线段和最小问题,;利用几何画板的度量与计算,点的动态功能逼近目标,接着利用轴对称将线段和最小问题转化为“两点之间,线段最短”的问题,然后再利用“三角形三边关系”对作图进行证明,表明了数学研究的一个基本流程,即利用信息技术对目标进行猜想,然后利用几何知识进行性逻辑证明,最后再应用。
八年级学生不重视学习方法,不注意归纳总结,不会思考,更不善于思考,只懂得机械的重复做题,浪费了大量的时间和精力,学生学的辛苦,毫无快乐可言。本节课通过利用数学软件几何画板,引导学生学会学习,学会思考,提升学习兴趣,从而使其感受到学习的快乐,避免死做题,读死书,以达到“教”是为可不教的目的。
1、知识与技能目标:
能将实际问题中的“地点”、“河”抽象为数学中的“点”、“线”,把实际问题抽象为数学问题。能利用轴对称将同侧问题转化为异侧问题,找到使路程最短的饮马点,能利用几何画板构造出饮马点。
2、过程与方法目标
通过几何画板研究,培养学生研究数学问题的方法,既能利用工具对使距离最短的饮马点进行猜想,也能通过逻辑推理证明找出让距离最短的饮马点,学会猜想、验证、应用的数学研究方法。
3.情感态度与价值观
通过本节课的学生体会数学的对称美,以及数学来源于生活又应用于生活。
重点:利用几何画板研究最短距离,使用轴对称将同侧问题转化为异侧问题,培养学生解决实际问题的能力。
难点:如何将同侧问题转化为异侧问题;在实际问题中运用最短路径模型灵活解决问题。
探究“将军饮马”问题
![]()
A、B两定点异侧 :两点之间,线段最短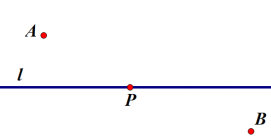
A、B两定点同侧 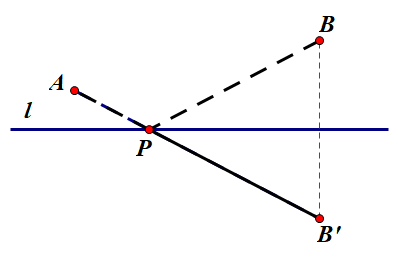
将军饮马模型:两定一动轴对称。
教学过程 | 技术应用 | 设计意图 |
(一)情景引入 师:同学们,今天我们来帮牛将军解决问题,一起探究将军饮马问题(板书课题) 插入视频(视频故事引入) 将军过河上班的故事。 师:因为什么? 生:两点之间,线段最短。 教师引导进入下一个环节。 (二)探索新知: 视频继续播放将军骑着宝马去上班的故事。播放完后提问: 师;牛将军遇到了什么问题? 生:牛将军要先去河边饮马,再去上班,要怎样才能不迟到。 师:怎样才能做到不迟到? 生:路程要最短。 师:路程最短,最关键的是什么? 生:饮马的地点。 教师引导进入下一个环节。 1、 解决问题 师:同学们说的很好,我们可以把实际问题抽象为数学问题,如图所示,P的位置不固定,那P在哪里的时候会让路程最短呢?我们一起用几何画板来探究下。请大家看到电脑里的路线图,改变P 的位置发现什么?请一位同学到黑板上演示。 学生探究。探究完后让板演的同学分享自己的发现。 其他同学点评。 师:通过刚才的探究,大家能知道点P的具体位置吗? 生:不知道。 师: 小组内部互相交流讨论,在草稿本上画出最短的路线图,以及喂马地点。 教师巡视,并适当指导讨论,然后利用希沃同屏功能上传学生所画的图形到白板上,并让该学生讲解理由。 教师总结。 IT教室:几何画板验证结论 学生选择性的观看电脑里微课,学习用几何画板画出上面将军饮马模型的图形,然后拖动直线上的点,验证将军饮马模型。 2、证明结论 用下面的图形解释依据。
(三)、课堂小结 将军饮马模型: 两定一动轴对称。 画图步骤: 1.做出B点的对称点 1.连接对称点与A点。
(四)、布置作业 已知,D、E两点分别是三角形两边AB、BC上的点,能在AC上找到一点P,使△DEP的周长最小。
| 利用网络搜索的视频,经过剪辑,服务于课堂,作为视频讲故事,复习回顾。
利用视频引入问题。
使用几何画板,利用动态功能感受数据变化。
在讨论过程中使用希沃计时器倒计时
利用希沃的同屏,展示学生的思考成果。
微课引导学生利用几何画板做出图形,利用动态性验证证明的结果。 | 通过视频讲故事,复习回顾“两点之间,线段最短 ”,抓住学生的 眼球,吸引学生。
继续接着讲故事,激发学生的兴趣,视频末尾留有疑问,激发学生的求知欲 。 此处在于引导学生分析实际问题。 给与学生思考与展示的机会,增加课堂的互动性。同时也是让学生主动思考,发现问题。
利用倒计时,让学生能更好的把握时间,提升效率。
学生感受信息技术的益处,帮助学生展现自己,同时创造机会培养逻辑推理的核心素养。让学生说明理由,给与了学生展示的机会,培养学生 的综合素质能力。
微课精简,内容通俗易懂,学生易于接收,容易模仿,便于学习使用几何画板。 课堂小结学生对知识有个系统性的认识,重点知识重点掌握。 课后练习紧扣主题,帮助学生应用所学,掌握知识。 |
设为正确答案