- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



圆的周长计算在实际生活中有着广泛的应用。教材从学生熟悉的生活实际情景引入,引导、帮助学生理解周长的概念,自主探究圆周长的计算方法,学生在解决实际问题的过程中感受方法多样性和“化曲为直”的转化思想,使得周长概念的内涵清晰,直观。学生在多样化的探究中,学生的动手操作能力和实践能力得到进一步的发展。教师进一步引导学生提升思维层次,寻求圆周长计算的一般方法,通过实验发现圆的周长与直径的关系,找到圆周率,在实验探究的基础上得出圆周长的计算公式。
学生已经初步认识了周长的含义,并学习了长方形正方形的周长的计算,且知道圆是日常生活中常见的图形。先让同学们进行课前小实验,知道圆的周长可以通过“化曲为直”的方法测量得到。也可通过直观演示,实际操作帮助学生解决问题。但圆是曲线图形,是一种新出现的平面几何图形,这在平面图形的周长计算教学上又深了一层。特别是圆周率这个概念也较为抽象,探索圆周率的含义以及推导圆周长计算公式是教学难点,学生不易理解。因此需要重点突破。
知识与技能:理解圆周率的意义,推导出圆周长的计算公式,认识圆的周长公式。
过程与方法:经历猜想、验证、得出结论等数学活动的过程,培养学生初步的演绎推理能力,形成解决问题的一些基本策略,培养学生的观察、比较、分析、综合及动手操作能力。
情感态度与价值观:了解我国古代数学家对圆周率研究的史实,进行爱国主义教育。
教学重点:推导并总结出圆周长的计算公式,知道圆的周长与直径、半径的关系。
教学难点:理解圆周率的意义。学会猜想、验证、得出结论的数学方法。

上节课我们学习了绳绕法和滚动法测量圆周长的方法,都是把圆的周长这条曲线转化成线段,然后通过测量线段的长度得到圆的周长。这种转化方法叫做“化曲为直”。
但是每次都用“化曲为直”的方法来测量圆的周长,这也太麻烦了。能不能用一个公式来总结出圆的周长呢?那我们首先就要明白,圆的周长和什么相关。大家不妨猜想一下。
生回答,圆的周长与直径相关。
教师板书:猜想。
1、我们今天就一起来探索,圆的周长与直径的关系。
2、我们通过一个小组活动来验证一下圆的周长和直径的关系。
小组交流:
1、测量小组中的圆形物品,量出它们的周长和直径,并算出周长和直径的比值(结果要求保留两位小数),把结果填入作业单的表格中。
2、你发现圆的周长和直径之间有什么关系?有没有什么规律?小组交流。
3、小组合作时间为5分钟。
4、初步认识圆周率。
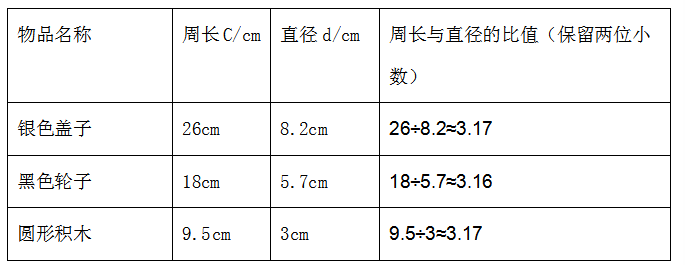
老师之前也量了这几个物品的周长和直径,算出了它们的圆的周长和直径的比值,整理成了表格(课件出示表格),看了几组同学和老师的的测算结果,你有什么发现?
5、最终,我们得出了结论,圆的周长总是直径的3倍多一些。
6、虽然都是3倍多一些,但怎么结果都不一样呢?这是什么原因造成的呢?由于测量时有误差,所以计算结果都不一样。
7、认识圆周率,总结公式。
(1)刚才同学们这个发现,其实早在2000年前,《周髀算经》就有提到过。介绍祖冲之。(视频播放)
(2)圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母 π 表示。它是一个无限不循环的小数,因此我们一般取它的近似数,π≈3.14(进行板书)
(3)总结公式:如果用字母C表示圆的周长,d表示圆的直径,那圆的周长公式用字母怎样表示呢?
板书:C=πd
提问:圆的周长还可以怎样求?
板书:C=2πr
1、趣味游戏
通过竞赛游戏,巩固圆周率和圆的周长公式,更加深入地理解圆周率的意义。
这节课我们学习了什么?你是怎样推导出圆周长与直径的关系的?圆周长的计算公式是什么?
这节课我们通过猜想,验证,得出结论这三个步骤,发现了圆周率,得到了圆的周长的计算公式。
设为正确答案