- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节课以“造桥选址”为背景,开展对“最短路径问题”的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用平移将线段和最小问题转化为“两点之间,线段最短”问题。对它的学习和研究,有助于对最短路径问题的分析、解决。为今后在求立体图形、圆、平面直角坐标系中求最值问题提供了方法。
学生在七年级和上节课的学习过程中,已经掌握了用与最值有关的公理、定理解决问题的推理能力。“造桥选址”是实际生活中的极值问题,在这个问题中,平移起了一个桥梁作用,学习过程的本质是推理与化归的过程。有助于提高学生的推理能力、应用意识;分析问题、解决问题的能力。
1.引导学生解决造桥选址问题中的最短路径问题;
2.培养学生的推理化归的能力,化未知问题为已解决问题;
3.通过模型的建立,帮助学生提高分析问题及解决问题的能力。
重点:利用平移将造桥选址问题中的最短路径问题转化为“两点之间,线段最短”问题。
难点:如何利用平移将未知问题:最短路径问题中的造桥选址问题转化为已解决的“两点之间,线段最短”问题。
板书设计:

“白日登山望烽火,黄昏饮马傍交河。”这首诗出自唐代诗人李颀的《古从军行》,诗中隐含着一个著名的数学模型:将军饮马之最短路径问题。我们是如何解决将军饮马之最短路径问题的呢?

学生回答;
方法小结:①通过轴反射,将直线同侧两点转化为直线异侧两点;
②利用两点之间线段最短,找出P点的位置。
设计意图:用古人的诗导出将军饮马模型,激发学生的兴趣,让学生初步感知,为引出最短路径问题中的造桥选址问题做铺垫。
生活中除了将军饮马问题中涉及到求最短路径问题,其实还有很多这样的情形,比如说造桥选址。
例题1:如图,A点为浏阳河对面的长沙特色茶颜悦色店,B点为一中双语实验学校,现在要过河去茶颜悦色买奶茶,如果给小明一次设计桥梁的机会,请问桥MN建在何处,使得小明到达茶颜悦色的路径最短?(其中河的两岸是平行的,桥与河垂直)
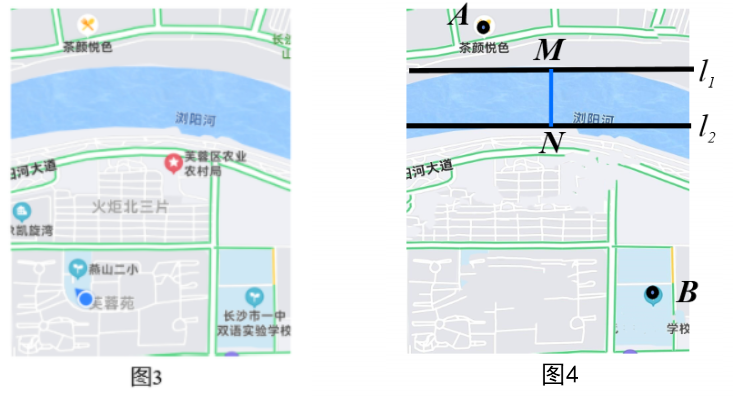
问题1:这是一个实际问题,我们首先要做什么?
学生:将实际问题抽象为数学问题
追问1:我们可以用一个怎样的几何图形来描述以上问题呢,请同学们画图?
学生画出图5
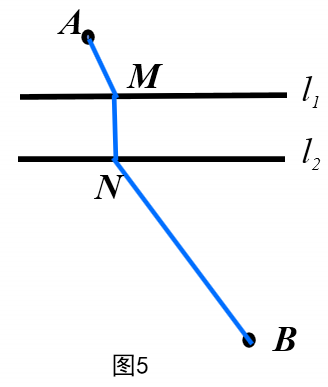
追问2:请结合几何图形用数学语言来描述这个问题。
模型建立:
如图,直线l1//l2,点M为直线l1上的一个动点,MN ⊥l2,交直线l2于点N,当MN 位于什么位置时,AM+MN+NB最小?

设计意图:让学生学会将实际问题抽象为数学问题,通过建模,将最短路径问题抽象为“线段和最小的问题”,培养学生直观想象,数学抽象,数学建模的核心素养。

几何画板上实操,通过动态演示追问学生以下问题
追问3:问题中要求桥梁MN建在何处,可以使AM+MN+NB最小,移动桥梁的位置,有哪些线段的长度发生了变化呢?
学生:AM、NB
追问4:由于MN是定长,所以要求这三条线段的和最小,实际可以转化成什么问题呢?
学生:求桥MN在何位置时,可以使AM+NB最小。
追问5:那MN在什么位置时,可以使AM+NB最小呢?我们来看一看,线段AM和BN在位置上是怎样一种情况?
学生:没什么特殊的联系,是分散的一种状态
追问6:那么我们能否通过一种位置变换使AM和BN转化为一条折线呢?
学生:小组讨论
追问7:将河岸l2向上平移与河岸l1重合,AM,BN的长度有没有发生改变?是否可以转化为折线问题?
老师制作教具,通过几何画板动态展示,让学生直观的感受问题的转变过程。
追问8:在现实生活中,我们是没办法通过上述平移使桥梁MN消失的,那在桥梁不消失的前提条件下,可否通过平移将桥梁的位置进行转移?
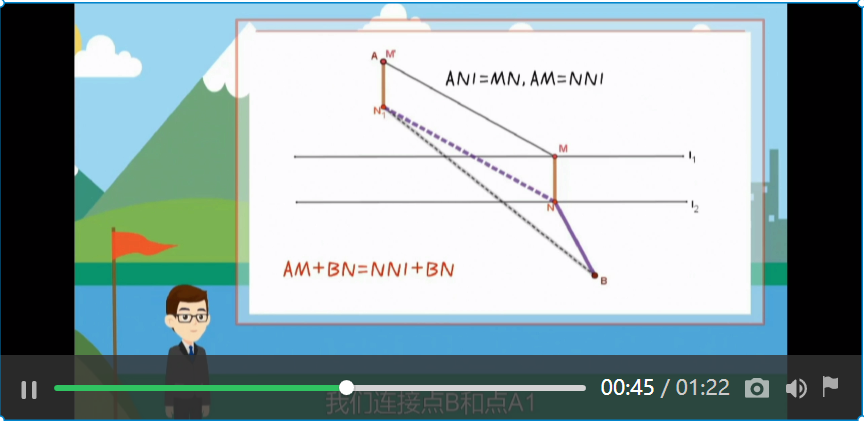
学生先自行思考并作图,请同学上台展示,并借助信息技术手段,通过微课,让学生直观感受问题的化归过程。
设计意图:通过平移,实现未知问题向已解决问题的转化:最短路径问题中的造桥选址问题转化为已解决的“两点之间,线段最短”问题。通过层层问题的递进设计,降低问题的难度,渗透转化思想,提高学生分析问题、解决问题的能力以及逻辑推理的数学学科核心素养。
如图,线段MN为直线l上一条运动的线段,且MN长度为定值,从定点A到M经过MN再到定点B,怎样确定MN的位置能使所走的路线AM+MN+NB最短?
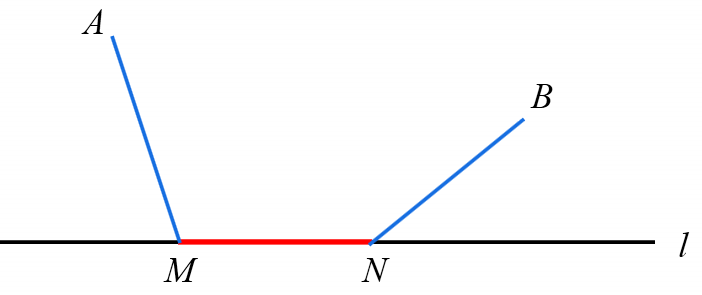
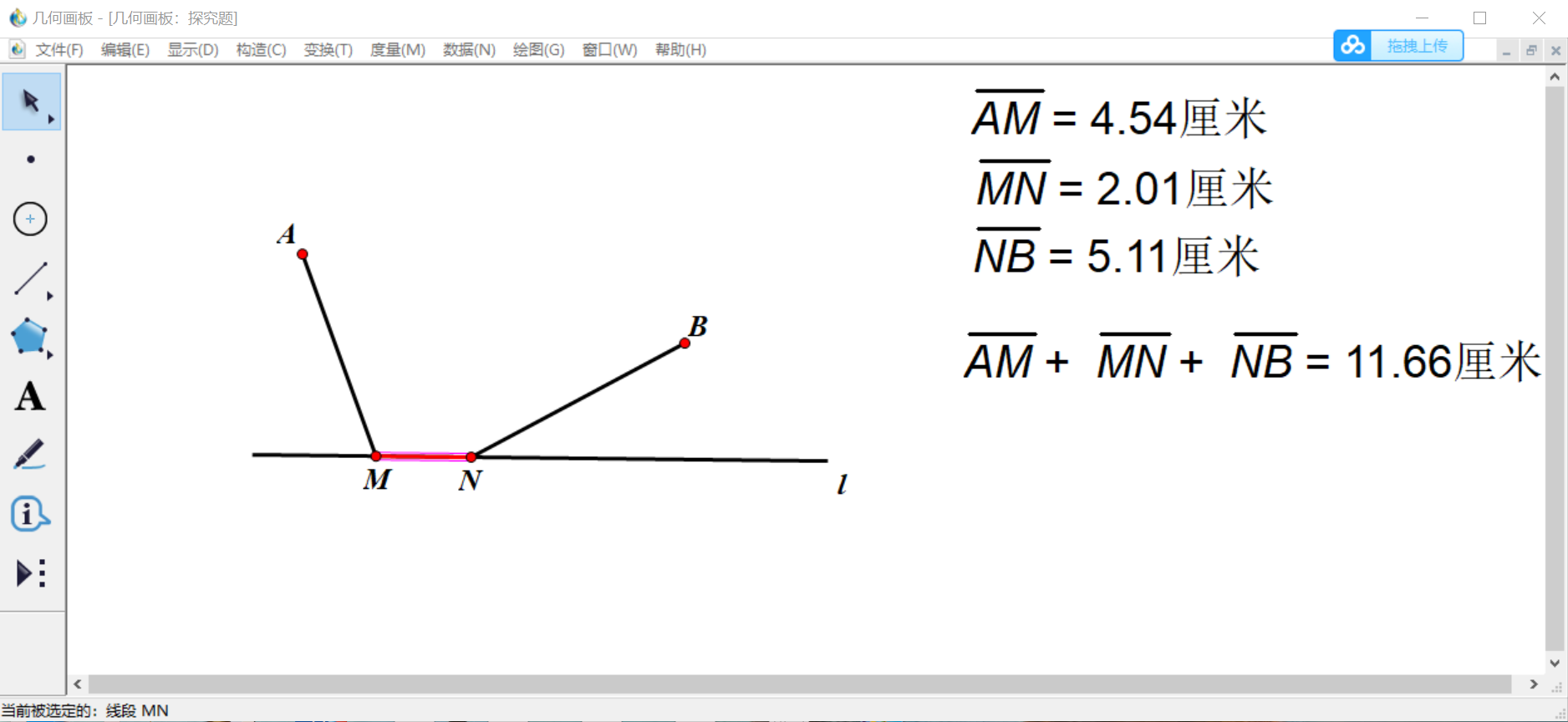

几何画板动态演示 微课讲解
设计意图:拓展延伸,实际上是通过平移的方法,构造将军饮马模型,是转化思想的深层渗透。意在让学生真正的学有所获,拓展学生的思维能力,以及提高学生分析问题、解决问题的能力。
(1)本节课研究问题的基本过程是什么?
模型建立:如图,直线l1//l2,点M为直线l1上的一个动点,MN ⊥l2,交直线l2于点N,当MN 位于什么位置时,AM+MN+NB最小?
解决方法:①通过平移,构造直线异侧两点的模型;
②利用“两点之间,线段最短”化折为直。

(2)平移在所研究问题中起什么作用?
学生:转化的作用,通过平移,改变三折线的位置关系,构造了直线异侧两点的折线模型。
设计意图:锻炼学生的胆量,给学生展示的机会,培养学生归纳概括的语言表达能力。
设为正确答案