- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
1.了解基本不等式的推导过程，理解其几何意义与代数意义，并掌握基本不等式取得等号的条件。
2.求出一些简单函数的最值（最大最小值），并能解决一些较为简单的实际问题。
3.培养逻辑推理能力、严谨求实的科学态度，领略数学的应用价值，激发学习兴趣。
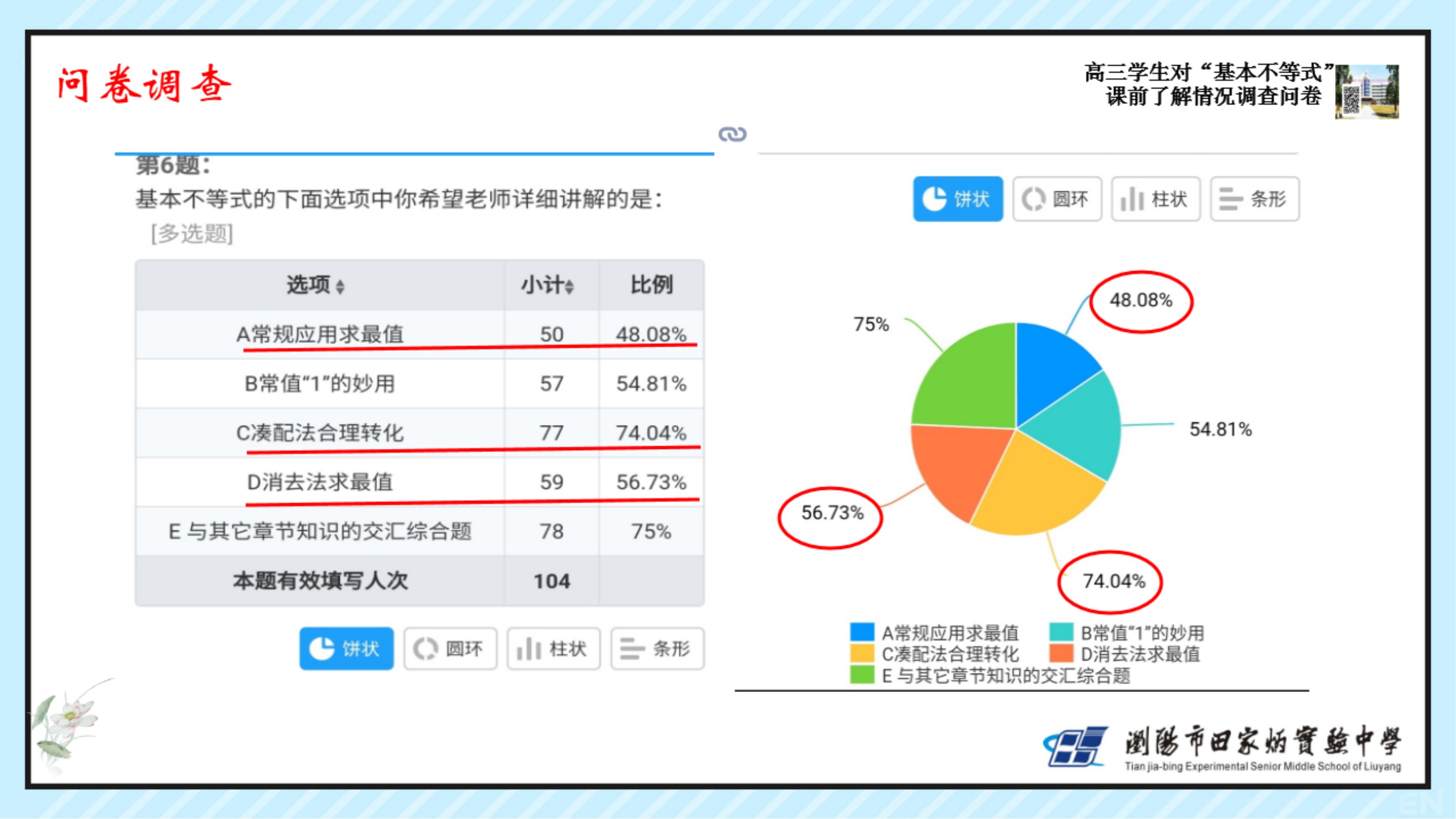
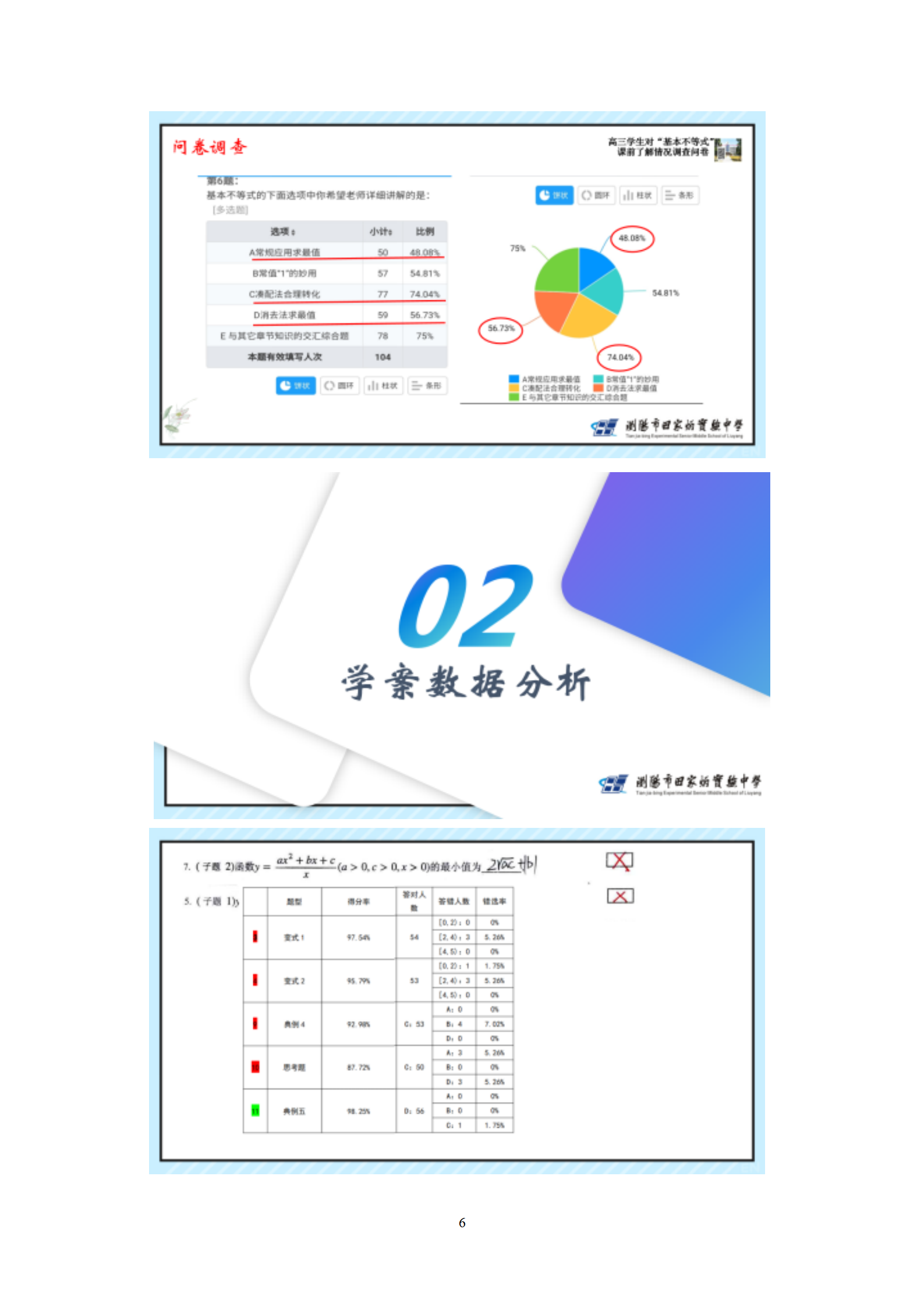学生能直接利用或简单变形运用基本不等式快速解决一些基本常规题
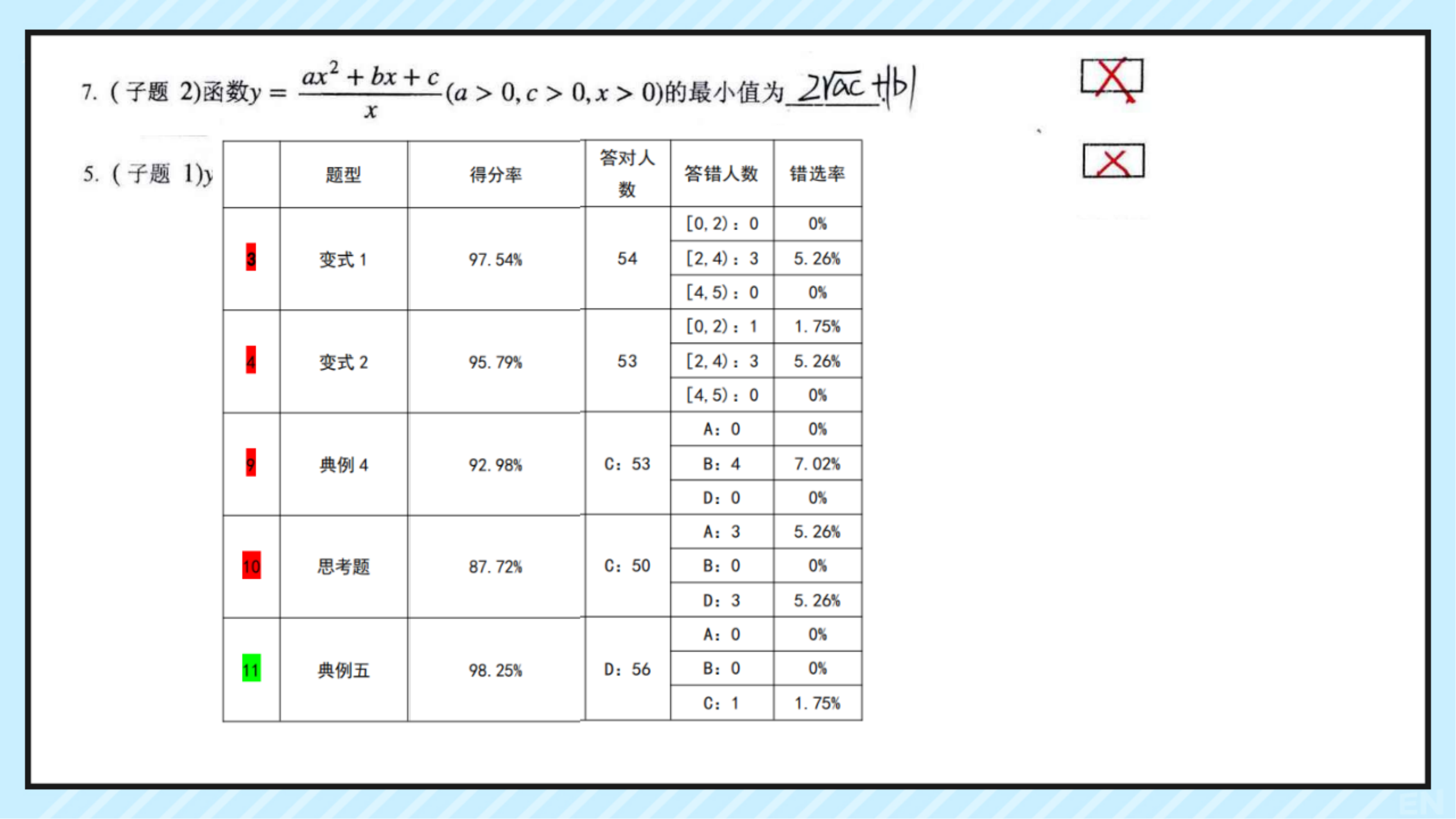
当出现变量增加，式子结构复杂，定值隐晦的问题以及实操的题都是学生的难点
要么很快做出，要么都不知道怎么想？同学之间没有多大的区分度。
出现简单题不看清题随意作答而导致出错。
4.畏难思想严重，只想等待老师来解决问题，而不能自主去合作解决问题
知识目标：
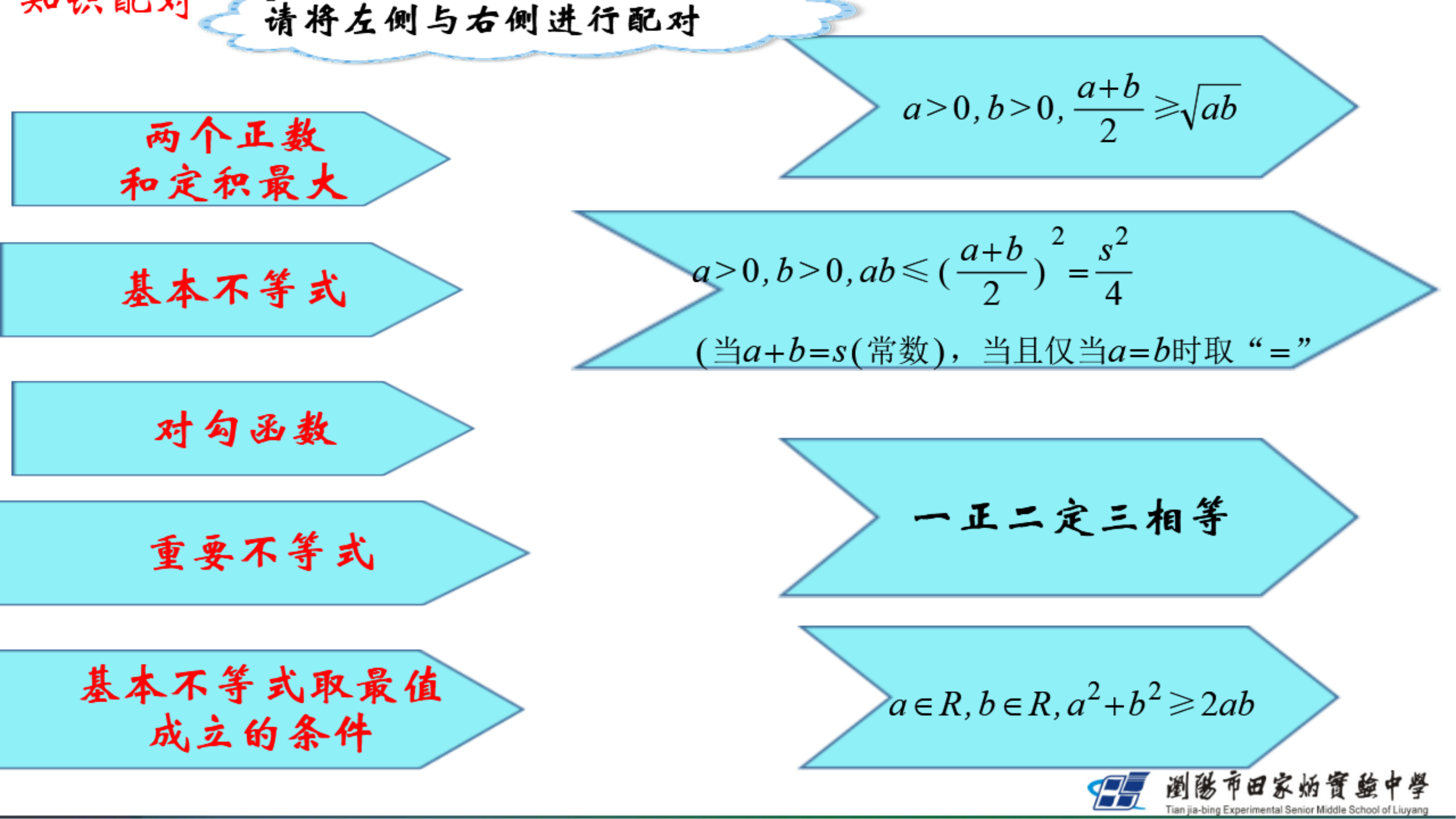
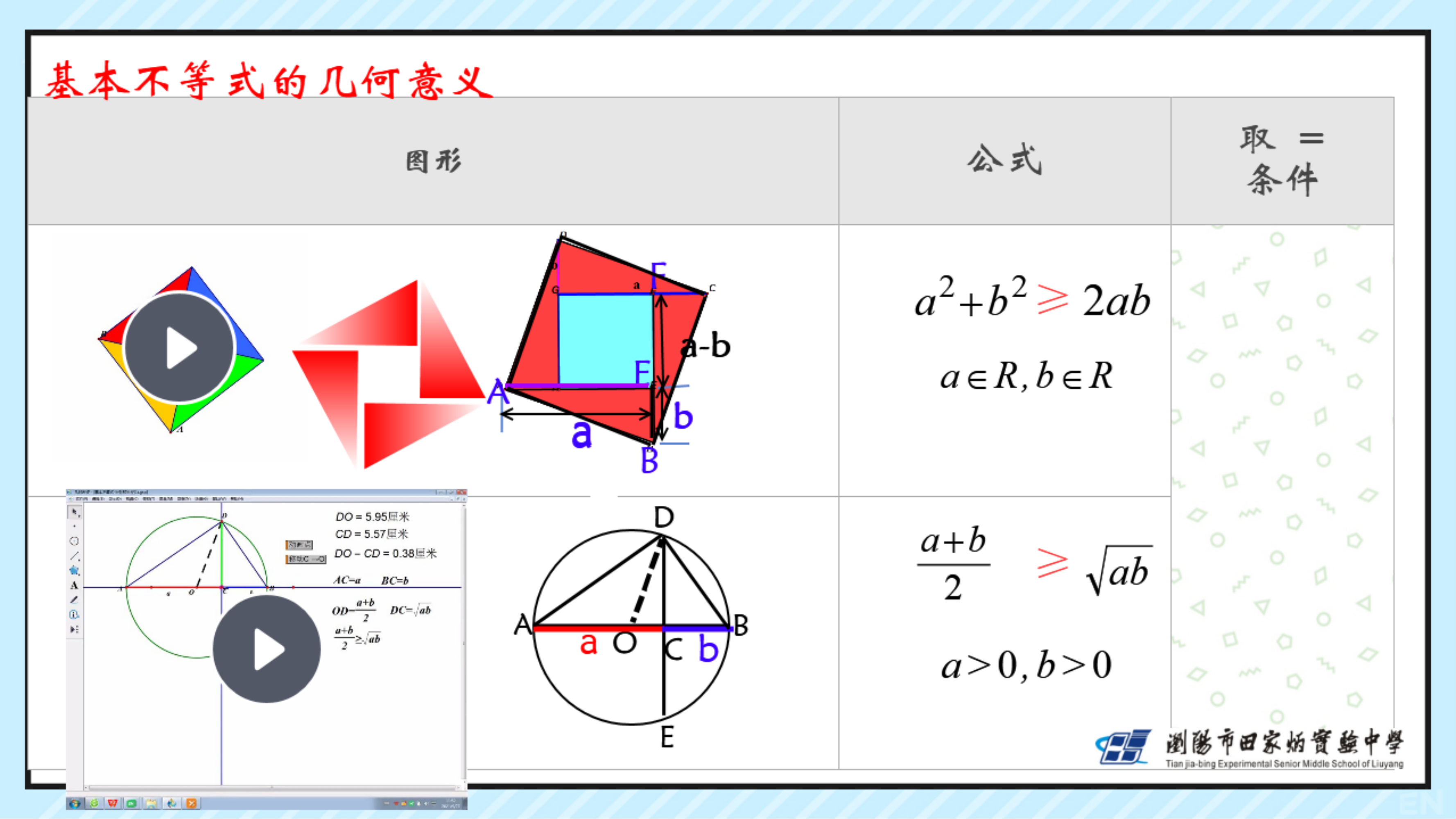
1了解基本不等式的证明过程。理解基本不等式的代数特征和几何意义。
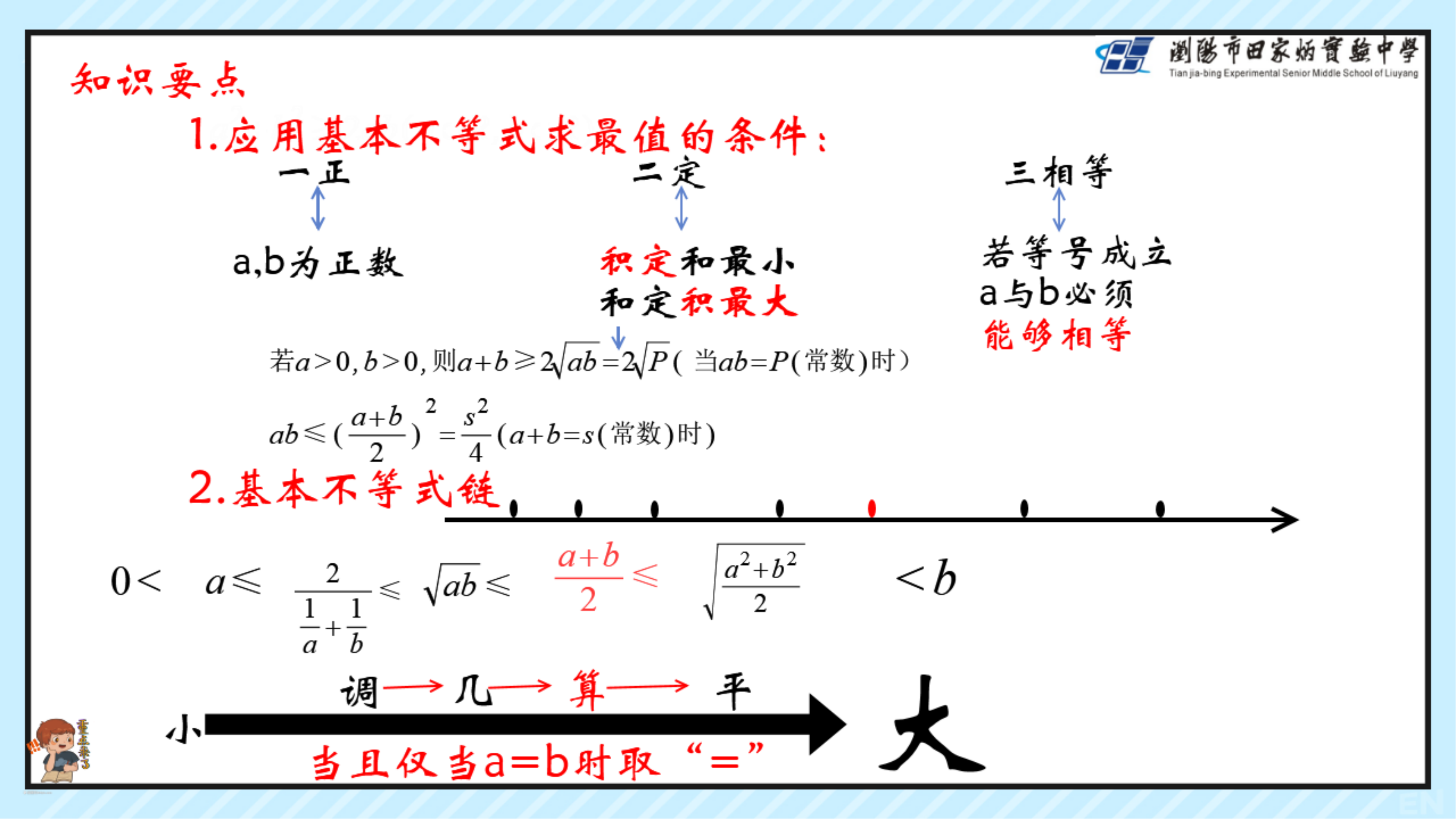
2.会用基本不等式解决简单的最大（小）值问题。
3.会运用基本不等式的本质特征把握问题的方向，运用合理的变形手段达到目的。
能力目标：
培养学生运算求解能力，数学建模能力以及逻辑思维创新能力。
素养目标：
培养学生数学抽象，逻辑推理，数形结合等数学核心素养。
一、教学目标：
1.通过对几何背景的了解加深学生对基本不等式的理解。
2.通过合作探究提高学生数学抽象与逻辑推理的能力。
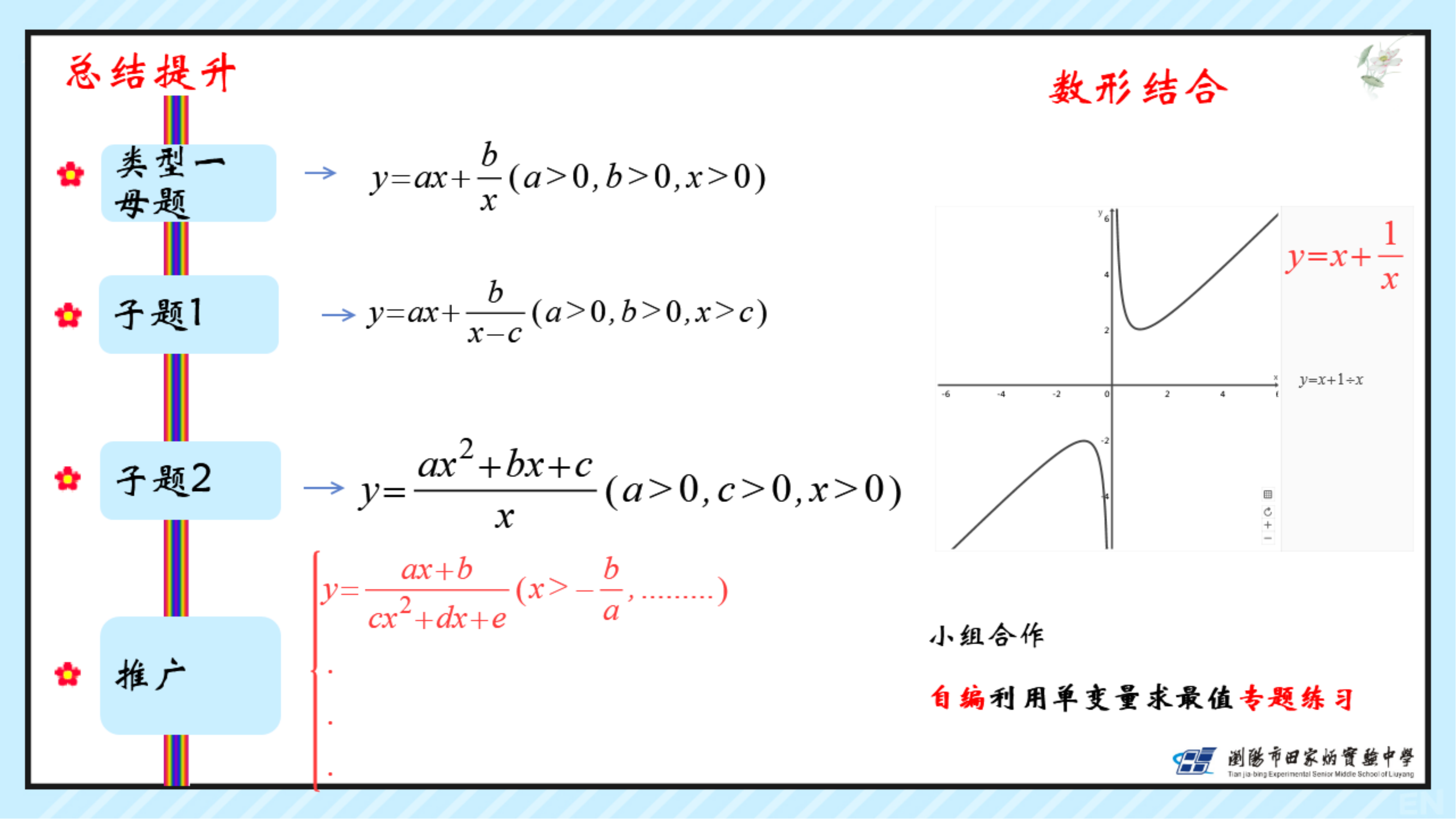
3.通过数形结合培养学生观察分析的能力。
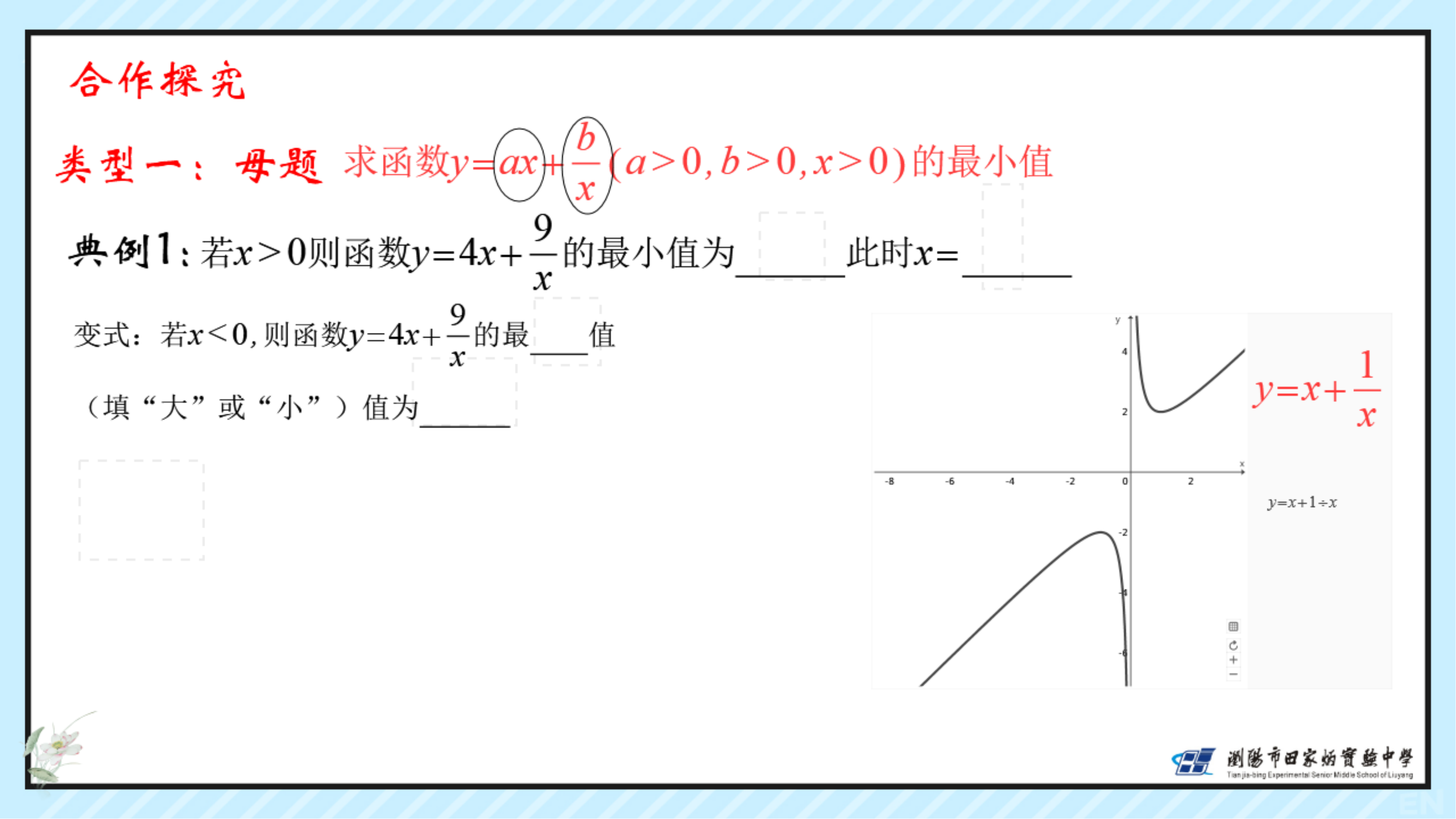
4.进一步掌握基本不等式；并会应用此不等式求某些函数的最值；能够解决一些简单的实际问题.
二、教学的重点：1.分析结构，合理变形。2.注意两个正数求最值的条件。
3.不能用基本不等式怎么办？
三、教学难点：合理变形巧妙凑配
利用基本不等式求最值，范围，值域。
灵活运用基本不等式解决与其它知识点交汇的问题。
利用基本不等式解决生活中的实际问题。
二、教学的重点：1.分析结构，合理变形。2.注意两个正数求最值的条件。
3.不能用基本不等式怎么办？
三、教学难点：合理变形巧妙凑配
设为正确答案
