- 时间点：
- 时 分 秒 当前视频时间点
- 问题：
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间：
- 时 分 秒 同锚点时间
- 错误跳转时间：
- 时 分 秒 同锚点时间
恭喜你，回答正确~
很遗憾，回答错误~
正确答案： ,您可以
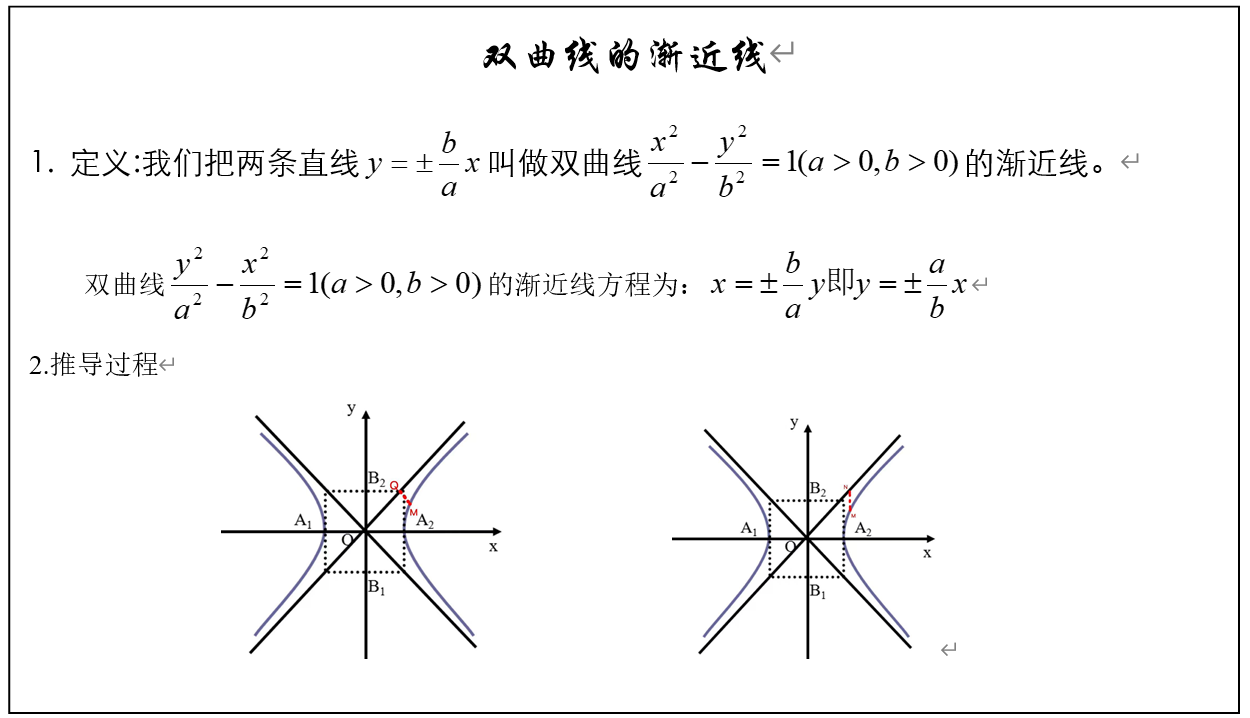
本节课时是高中数学人教A版（2019）选择性必修第一册第三章《圆锥曲线的方程 3.2 双曲线》第二课时——双曲线的渐近线，是在学生已掌握双曲线的定义及简单的几何性质的基础上，进一步探索和发现“为什么
是双曲线
的渐近线”。学生对渐近线还处于直接感受和操作确认的阶段，缺少对双曲线渐近线的完整认识。本节课应引导学生从图形的直观感受提升到严格的逻辑推理证明。进一步使学生理解和体会坐标法在解析几何中的应用。
学生在学习双曲线简单的几何性质时类比椭圆的几何性质可以得到，但双曲线中多了一个性质——渐近线，而教科书没有给出双曲线渐近线的严格定义，只是一种描述，而且出现地比较唐突，学生接受起来较为困难。所以这节课就是通过合适的问题引导，合理的呈现，并促进知识的有效生成，来使得双曲线的渐近线的知识发生、发展的过程与学生的认知过程真正的融合，在课堂教学中“出现”得更自然、更合理，从而实现学生的思维发展目标，培养学生的核心素养。
教学目标：
1.正确理解双曲线的渐近线的定义，能利用双曲线的渐近线来画双曲线的图形；
2.掌握由双曲线求渐近线和由渐近线求双曲线的方法，并能作初步应用，从而提高分析问题和解决问题的能力。
核心素养：
通过研究双曲线的渐近线的学习，培养学生的数学抽象，逻辑推理，数学运算等数学核心素养。
教学重点：
1.双曲线渐近线的几何特征；
2.双曲线渐近线的方程与证明。
教学难点：
双曲线的渐近线的证明过程的理解。
教师引导：根据双曲线的方程，类比椭圆的性质，我们可以得到双曲线很多类似的性质，其中对称性几乎是一模一样的，借助这些性质，我们是否可以更准确美观画出双曲线的图象呢？现在请同学们画出 
的双曲线的图象。
学生预设：画出双曲线的图象
教师活动：选出代表性的几个图，并用交互式一体机EN5投屏展示，带领学生共同对这些图作出对比与评价。
教师引导：接下来我们通过一个微课来了解为什么有的同学画的图形不准确？（播放微课）并且请同学们思考两个问题：1.双曲线的渐近线的几何特征是什么？2.双曲线的渐近线方程是什么？
（设计意图：要求学生画出双曲线的图像，并将图像投屏到智慧黑板上，让评析便捷化，能更快的发现问题，提高学生参与度，激发学习兴趣，再利用微课的引入，展示问题解决过程，这样就实现了技术支持的问题呈现与解决。）
【探究活动】
教师活动：利用“班级优化大师”随机点名学生回答以上两个问题，并且及时给出合适的评价；
学生预设：双曲线的渐近线方程是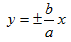
，它的几何特征是与双曲线无限接近但永不相交。
（设计意图：利用这两个问题引出这节课要探究的重点内容）
教师引导：我们利用数学学科软件Geogebra来直观地感受双曲线的几何特征。
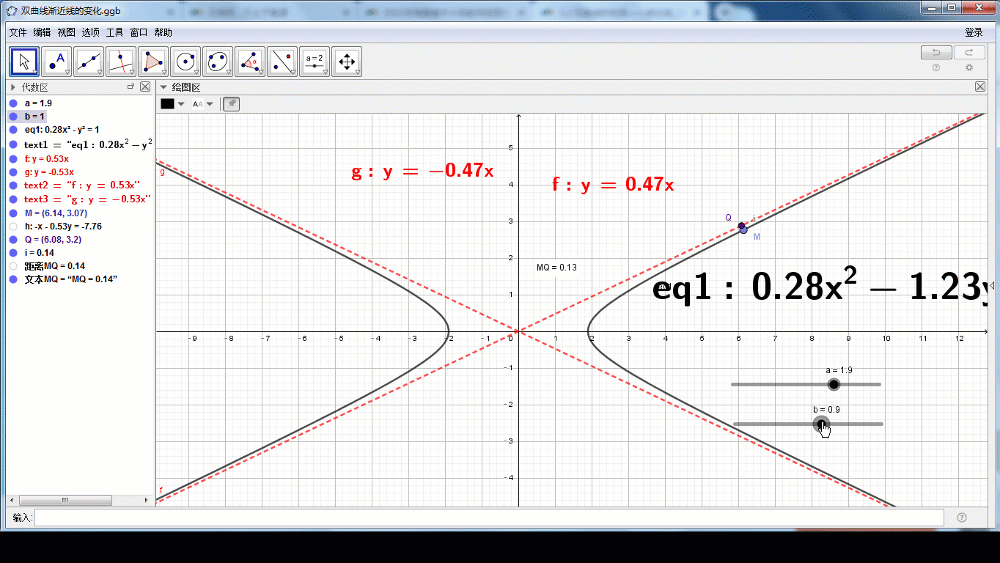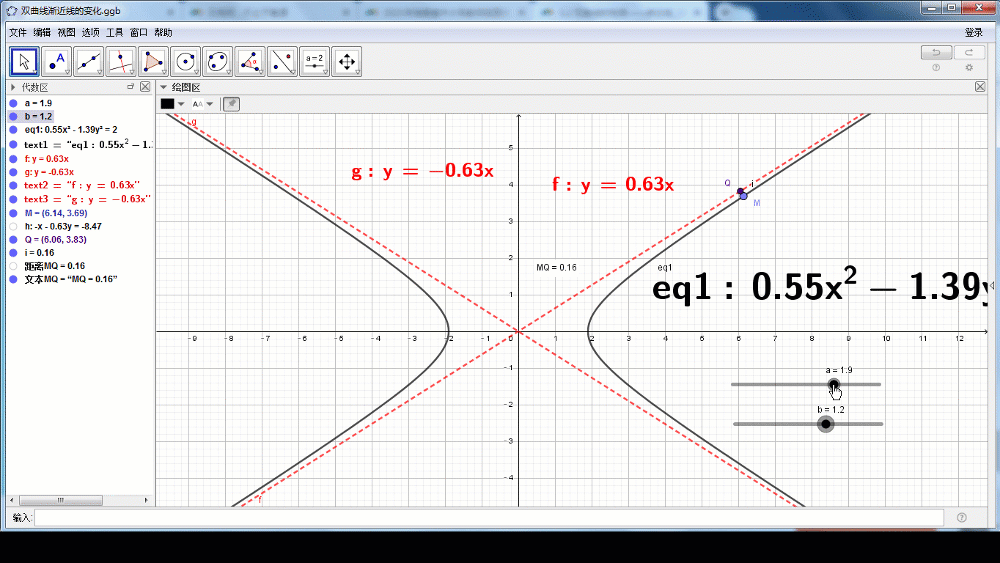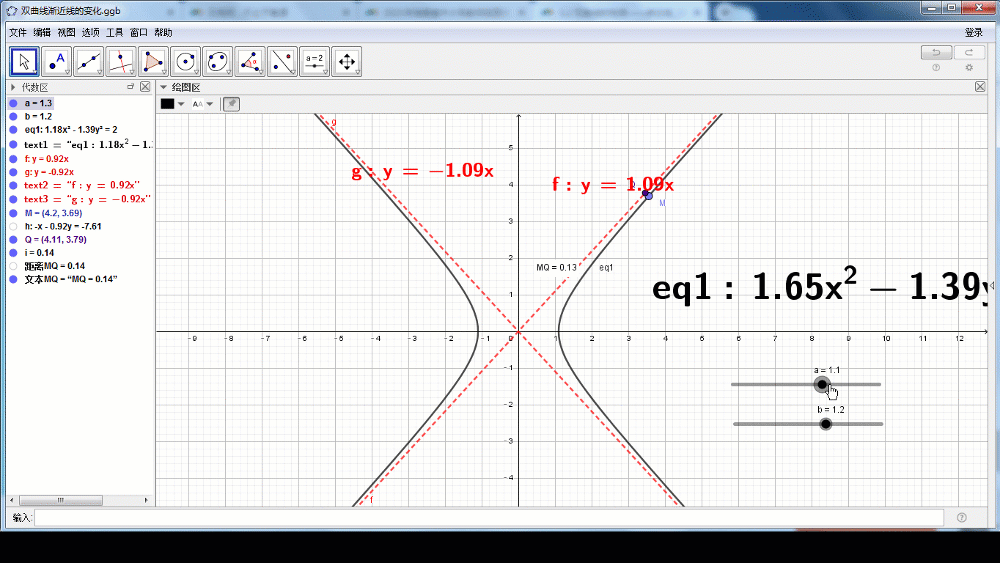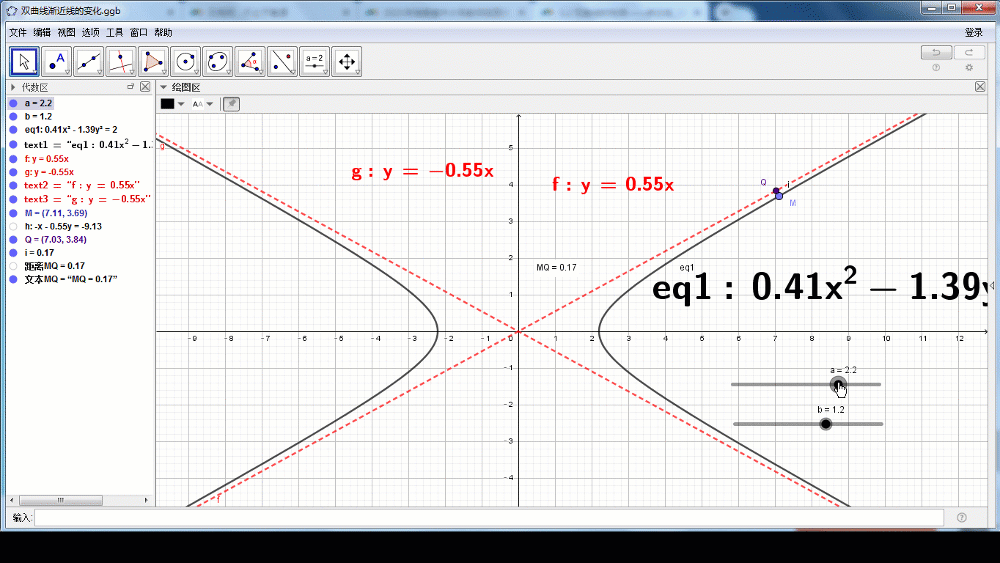
（设计意图：借助信息技术让学生先直观感受双曲线的几何特征，将原本抽象的内容变得直观具体）
教师引导：我们已经知道双曲线的渐近线的几何特征是与双曲线无限接近但永不相交，那么，我们如何去得到双曲线的渐近线方程，并如何证明呢？
（设计意图：引导学生用严谨的态度学习数学，使学生能实现从原有对渐近线直观感受到严格的逻辑推理证明。）
教师引导：由于双曲线具有对称性，我们不妨先探索双曲线在第一象限的情况。
在第一象限内，x、y均为正，所以方程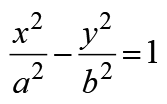
可变形为
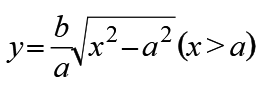，这样可以更方便地看出x与y变化趋势的相关性。
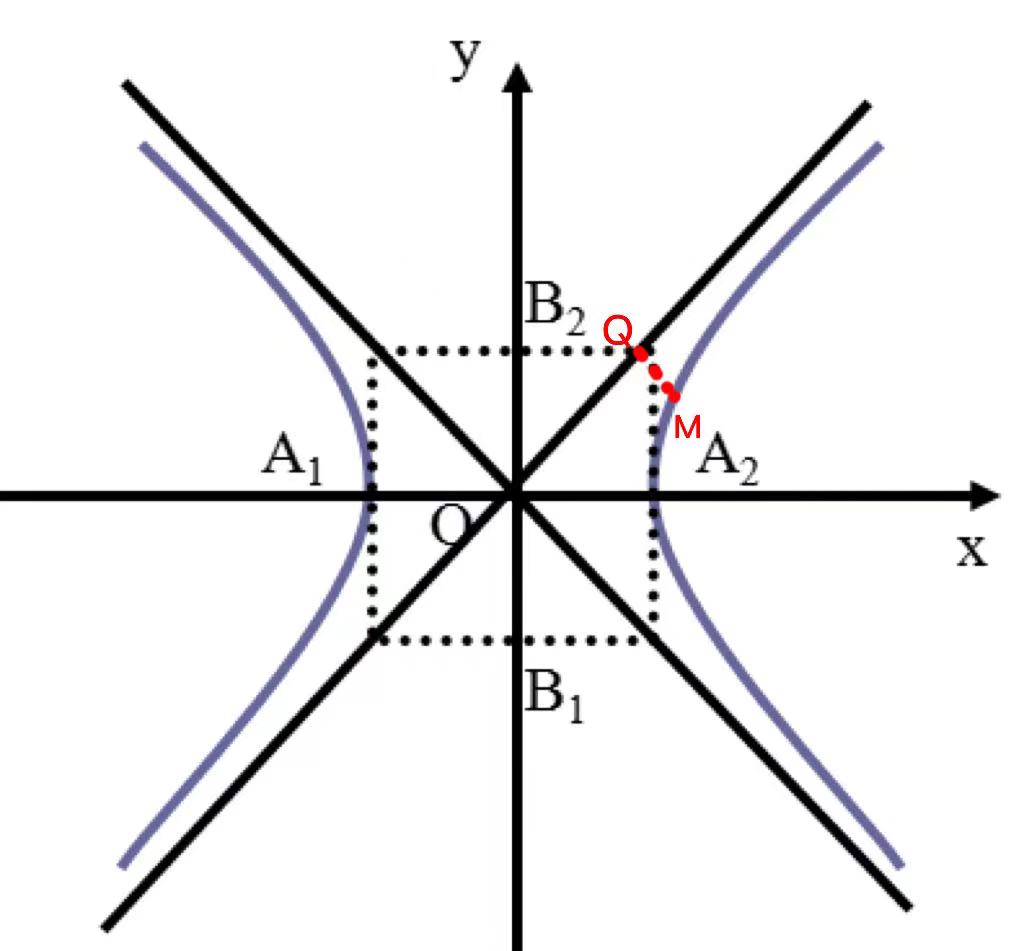
从上图可以直观看出，双曲线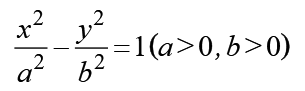
的各支向外延伸时，与这两直线逐渐接近。
教师引导： 如何衡量一条直线与一条曲线的接近程度呢？
学生预设：要通过距离来衡量。
（设计意图：层层设问，引导学生思考，把抽象问题具体化，由于对称性这一特点，放在第一象限研究，把复杂问题简单化，有利于学生数学意识和思维的养成，培养了学生独立思考的能力。）
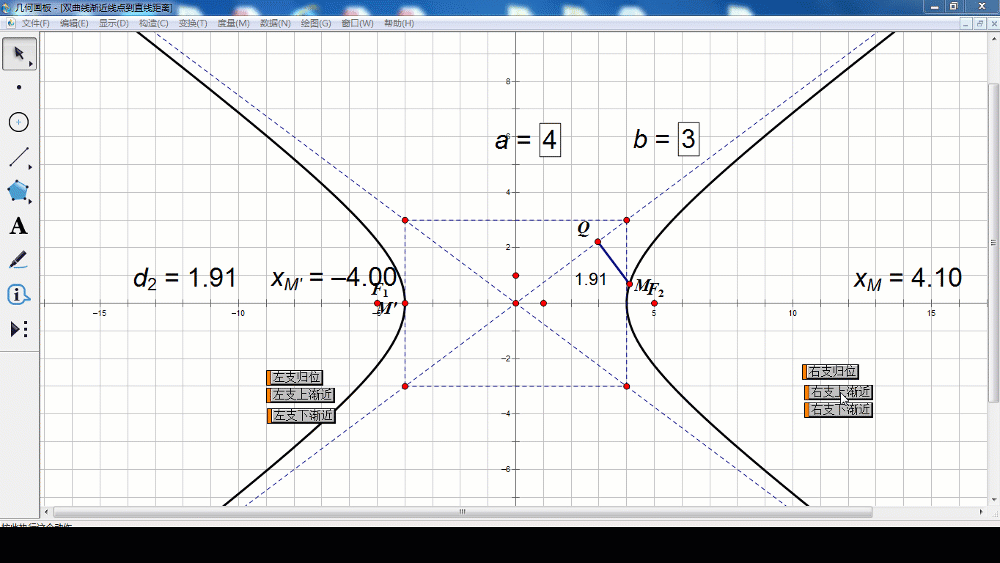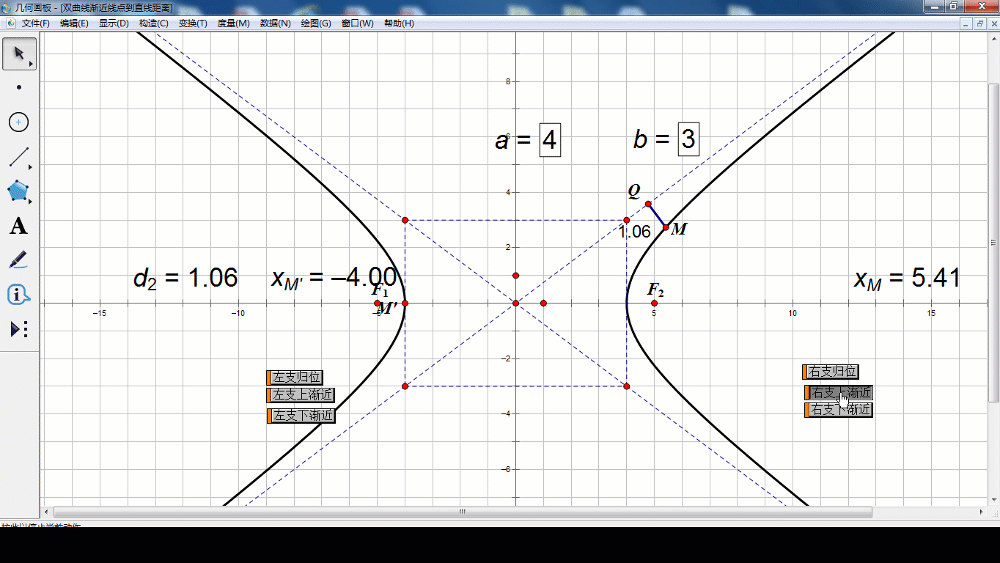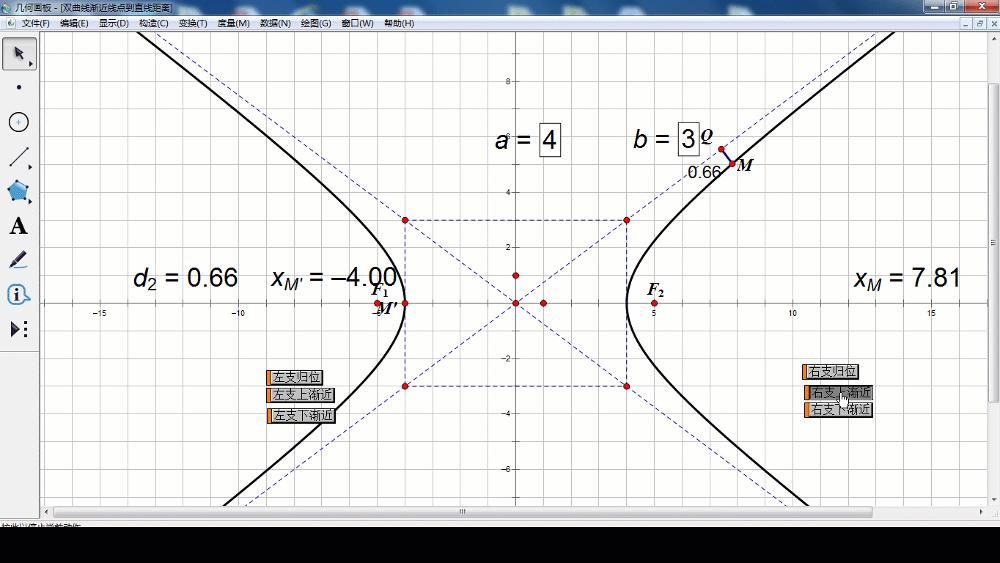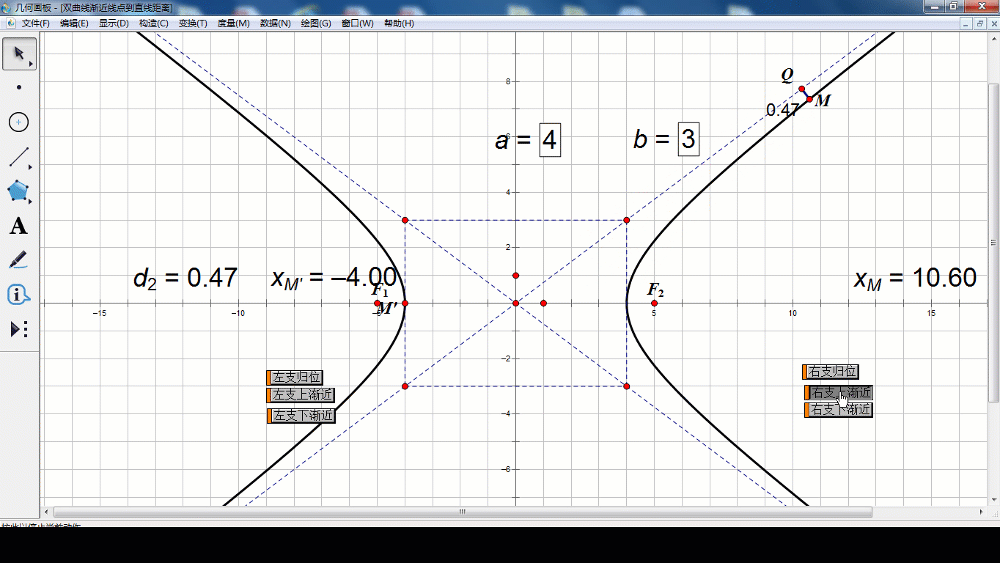
方案1（几何法）：在双曲线第一象限的图像上取点M，作MQ垂直于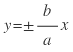
，用MQ的长度来表示双曲线与直线的距离。需用到点到直线的距离公式。
设M横坐标为
,从减少变量的角度来考虑，代入双曲线方程得M的纵坐标是
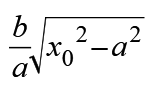而后利用点到直线的距离公式可得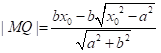
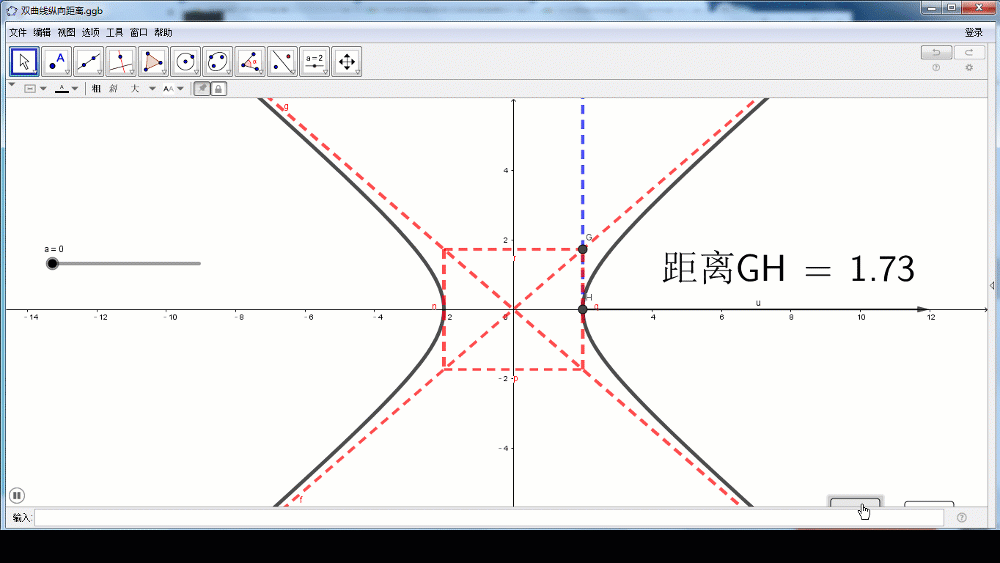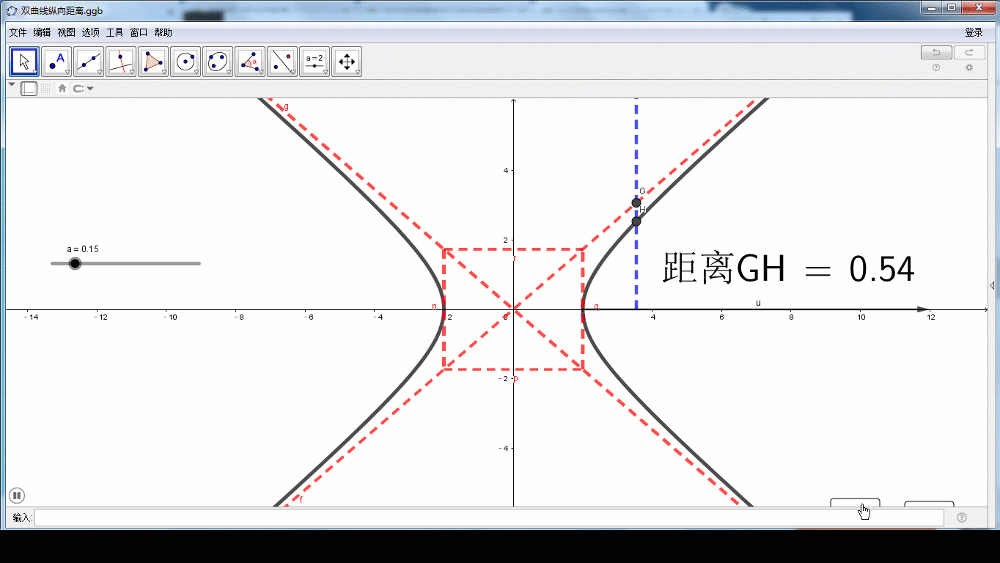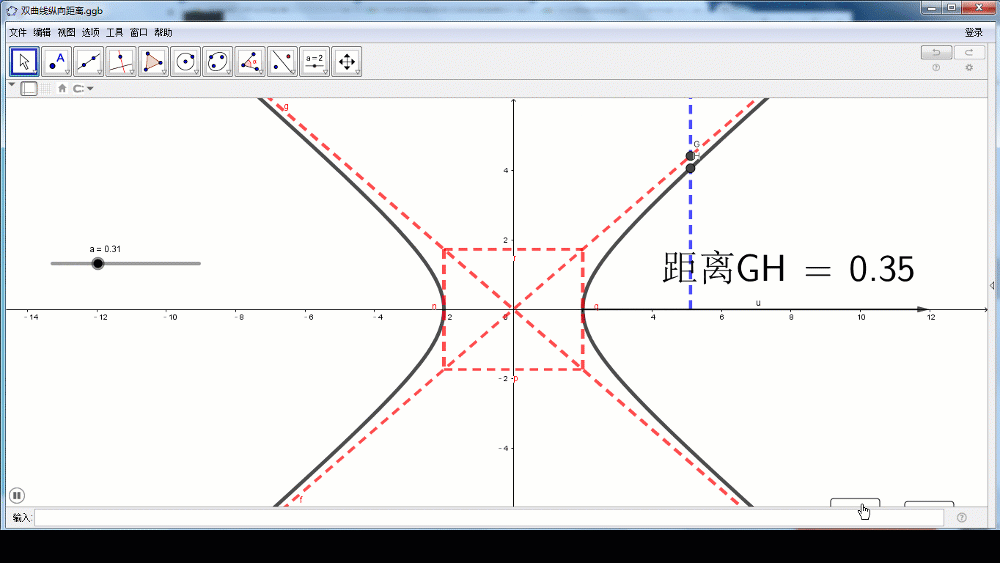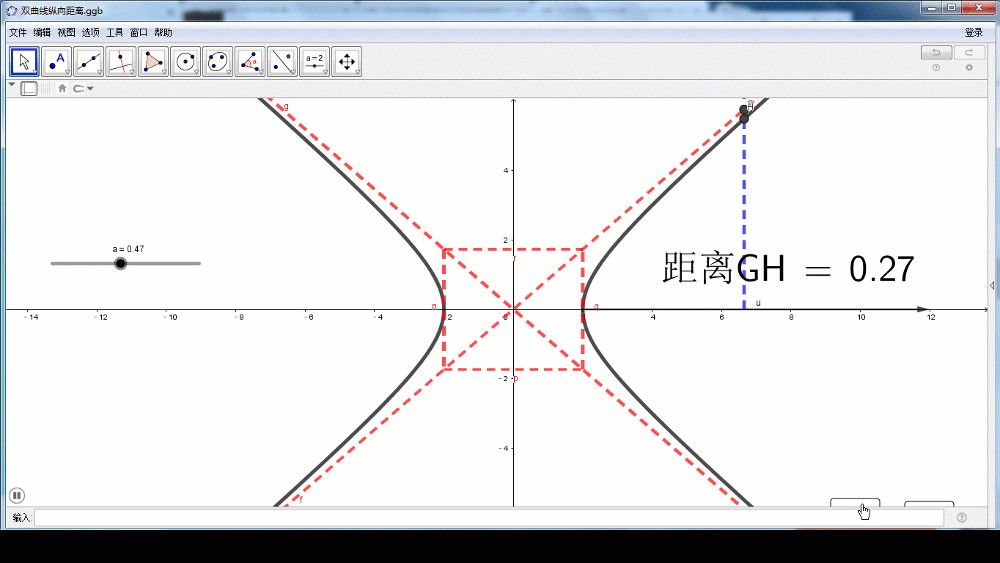
当x逐渐增大时，MQ的距离逐渐减小，x无限增大时，MQ的距离无限接近于0.也就是说，双曲线在第一象限向右上方延伸时，是从OQ的下方逐渐接近于射线OQ，但与射线OQ永远不相交。根据双曲线的对称性，在其他象限内，也有类似结论。
（设计意图：带领学生从形的方面来证明渐近线，增加学生对渐近线的深刻理解）
（师生活动：学生口述，老师板书，利用几何画板进一步展示几何法）
方案2（代数法）：
利用纵向距离也可以值得研究。作MN平行于渐近线交于N，由于MN与MQ成定倍数关系，因此可以替代MQ进行研究。
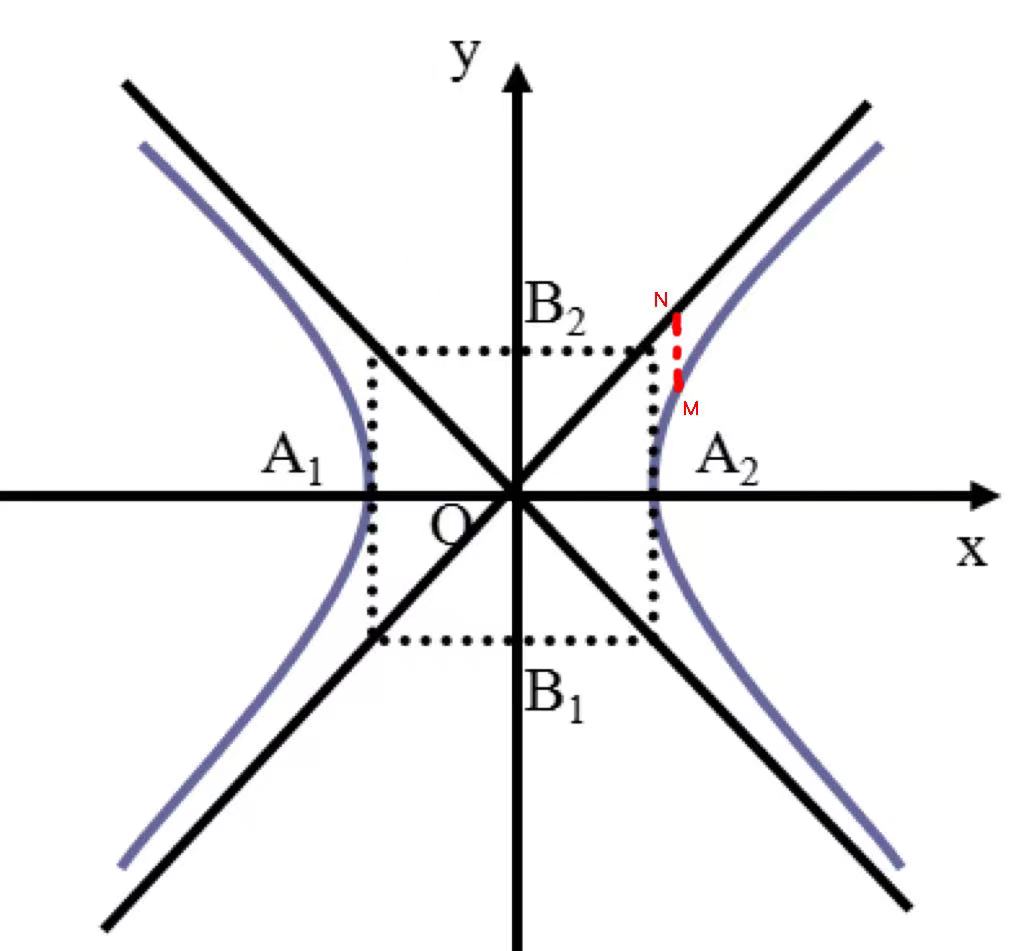
M、N的横坐标相同，这样以来MN的长度等于二者纵坐标的差。
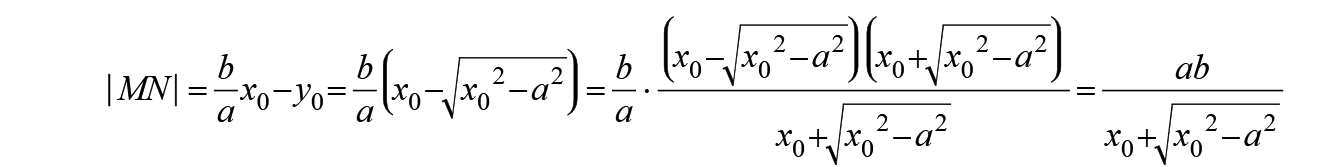
当x逐渐增大时，MN的距离逐渐减小，x无限增大时，MN的距离无限接近于0.
在其他象限内也可以证明类似的情况，我们把两条直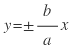线
叫做双曲线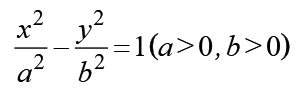
的渐近线。（板书定义）
（设计意图：方案一是从形的方面来证明，因此引入方案二从数的方面来证明，这样即可以发散学生的思维，让学生多思考，又体现了数形结合的数学思想）
（师生活动：学生口述，再借助GeoGebra进行动画演示）
教师引导：大家现在知道应该怎么快速准确的画出双曲线的图象了吗?
学生预设：先画矩形，再画渐近线，最后在画双曲线。
（设计意图：设计这样的一个提问既可以判断本节课的教学目标是否完成，又与课堂前面的引入前后呼应，使得整堂课完美呈现。）
课后作业
（设计意图：检验本节课的学习效果，巩固本节课的知识，同时使用二维码收集作业较之传统方法更便利）
设为正确答案
