- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



三角形的中位线选自湘教版八年级数学下册第二章第四节,它是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线、全等三角形、平行四边形等知识内容的应用和深化,又是以后的几何推理、证明中不可或缺的知识财富。在三角形中位线定理的证明及应用中,处处渗透了化归思想,它在今后的学习中有着重要的作用,并能拓展学生的数学思维。
整体来说,学生的知识迁移能力处于弱势,数学思想方法的灵活运用也有待提高。因此,本节片段课着眼于基础,注重能力的培养,积极引导学生首先通过实际操作获得结论,然后借助于平行四边形的有关知识进行探索和证明,使学生的优势得以发挥,劣势得以改进,从而提高学生的整体水平。
1、知道三角形中位线的概念,明确三角形中位线与中线的不同。
2、掌握三角形中位线定理探究过程中使用的数学方法与数学思想。
3、掌握三角形中位线定理。
重点:三角形中位线的概念和三角形中位线定理。
难点:难点是证明三角形中位线性质定理时运用转化的数学思想.

![]()

![]()
4.2 三角形中位线的性质定理探究
一、激趣导入
1、讲述古希腊泥板上的故事——父亲为如何将一块三角形土地均分给四个儿子而困恼,测量师给出了方案:连接三角形三边中点。
2、引入课题 三角形的中位线
二、探究新知
1、学习概念——三角形的中位线
展示概念:
连接三角形两边中点的线段,叫做三角形的中位线。
2、三角形中位线定理的探究
小组合作
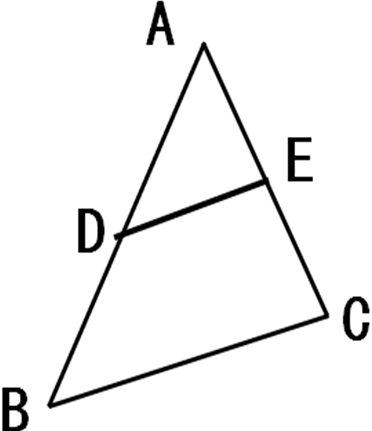
根据小组准备的三角形,绘制中位线,观察并测量数据,完成导学案,
通过在线投屏小组的成果,请小组上台猜测结论。
位置关系:DE//BC
数量关系:BC=2DE
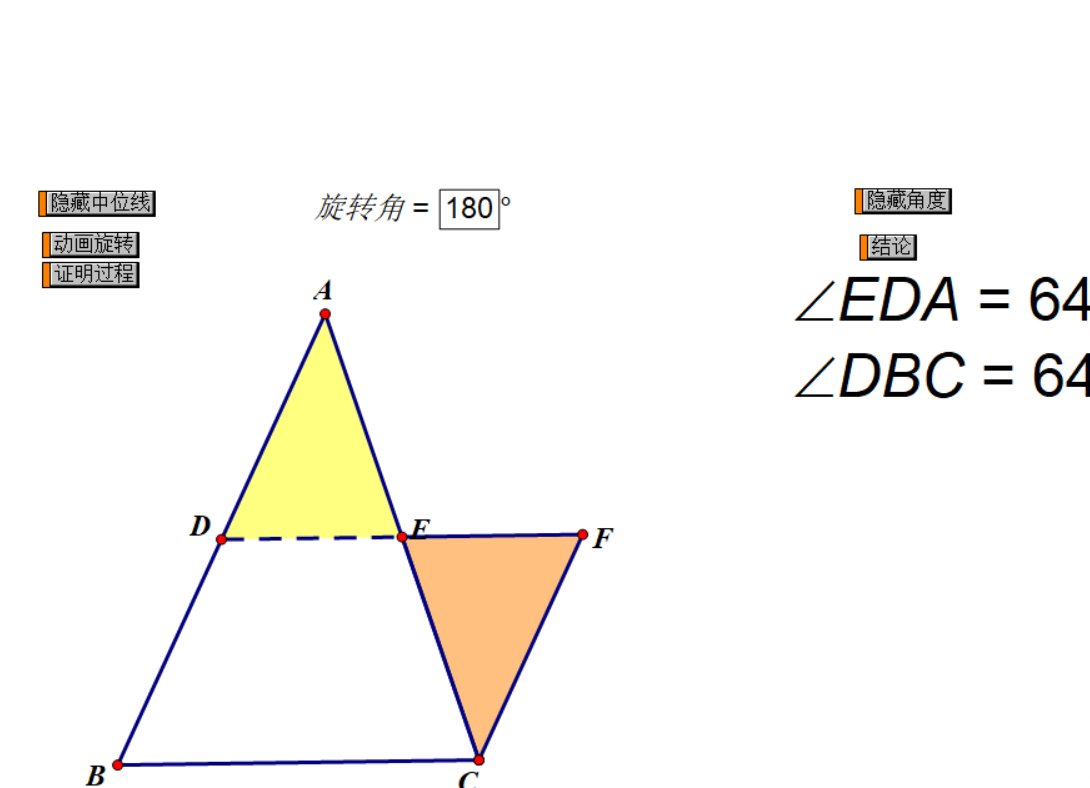
3、几何画板演示
利用几何画板动态演示,改变三角形大小(锐角三角形、直角三角形、钝角三角形),观察DE与BC的数量大小,和一组同位角的大小关系。
猜测,任何一个三角形的中位线,都平行于第三边,并且等于第三边的一半。
4、几何论证
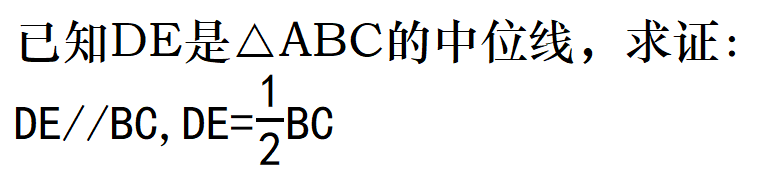
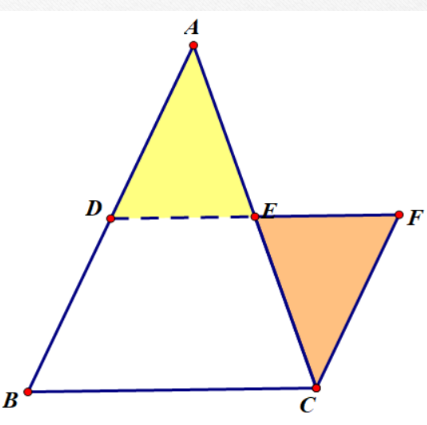
1、将△ADE绕点E旋转180°,得△CFE,观察四边形DBCF. 思考:为什么四边形DBCF是平行四边形呢?
(提示:通过转化思想,将三角形问题转化为平行四边形。从而得证。)
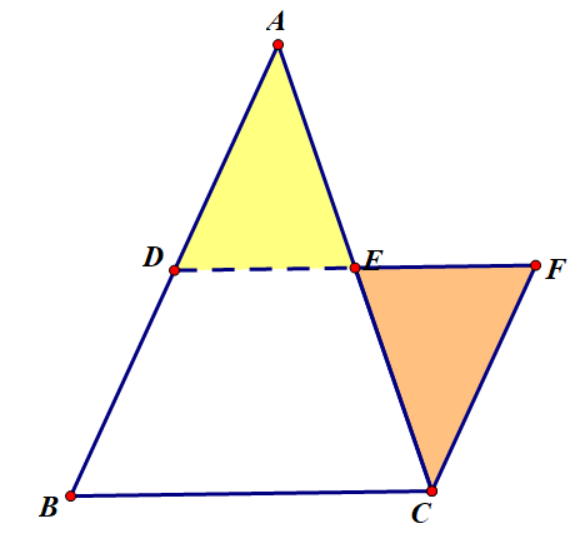
2、 请学生回答,教师板书证明过程。
证明:

三、推出三角形中位线的性质定理

四、回到古巴比伦泥板问题
回归到最初的古巴比伦石板问题。根据三角形中位线的性质容易得证四个小三角形全等。
板书如下:三角形中位线的性质探究
1、定义
2、符号语言

设为正确答案