- 时间点:
- 时 分 秒 当前视频时间点
- 问题:
-
- 选项一
设为正确答案
新增选项 - 选项一
- 正确跳转时间:
- 时 分 秒 同锚点时间
- 错误跳转时间:
- 时 分 秒 同锚点时间


恭喜你,回答正确~
很遗憾,回答错误~
正确答案: ,您可以



本节是人教版必修2第六章第1节的内容,圆周运动是学生在充分掌握了曲线运动的规律后,接触到的一个较为复杂的曲线运动,本节内容作为该部分的起始章节,主要向学生介绍圆周运动的几个基本概念,为后继的学习打下一个良好的基础。圆周运动是曲线运动的一种特殊情况,生活中随处可见,在学习过程中,只要注意观察和实验,并结合实际经验,很好地理解和掌握圆周运动、匀速圆周运动的概念,重点理解和掌握线速度v、角速度ω、周期T和转速n的意义及相互关系。而本节内容是在学生学习了圆周运动的基本概念之后,有了一定的基础之上,再进行模型的分析和深化。
学生已学习了曲线运动和圆周运动的基本知识,对描述圆周运动的物理量线速度、角速度、周期、频率、转速及物理意义已经掌握好。已为本节内容打下基础。通过一学期的高中物理学习,本班学生已经有一定的物理问题思维能力和物理模型建构能力,但是由于物理科目的特殊性,学生不容易理解解题思路和解题方法,基础仍旧薄弱,本堂课通过课堂动画演示的观察,引导学生归纳总结传动模型的特点。
1.通过对常见传动模型的分析对比,理解其特点,并能应用其规律解题。
2.通过将常见装置模型化,培养学生的建模能力。
皮带传动模型的理解和应用。常见模型的分类。
6.1 圆周运动——常见传动模型
1、皮带传动
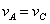 ,
,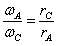 。
。
2、同轴传动
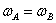 ,
,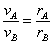 。
。
知识回顾:比较一个物体做圆周运动的快慢,需要用到哪些物理量?
线速度: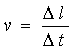
角速度: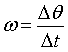
线速度和角速度关系: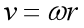
(学生回答)
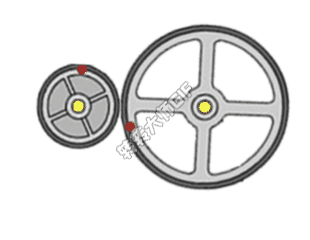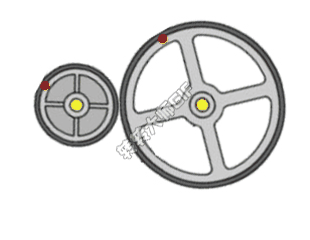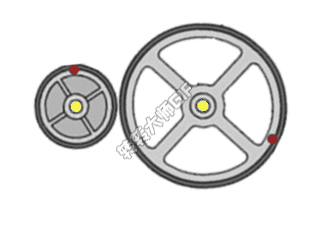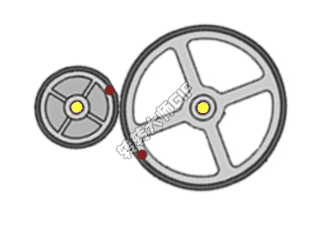
我们已经学习了圆周运动的基本概念,而在圆周运动中涉及到了很多传动模型,今天我们来学习常见的传动模型,首先来看到我们非常熟悉的自行车,自行车中就用到了传动装置,把装置简化成模型图。如下图:

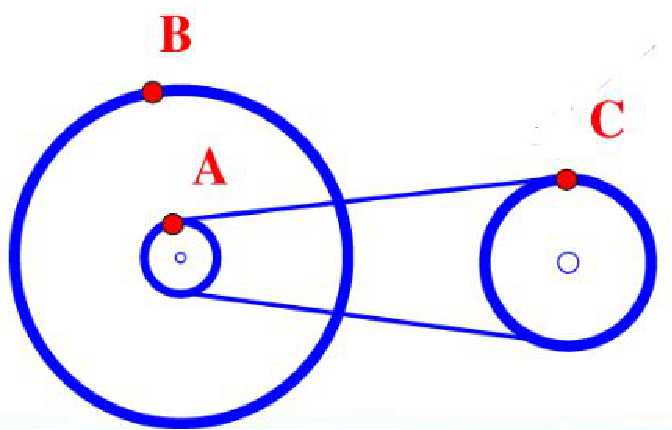
小轮和较大的轮通过铁链相连,小轮和大轮通过轴相连,ABC三点分别是三个轮子边缘的三个点,这三个点的线速度和角速度分别有什么关系呢?通过今天的学习就能解决这个问题。
(一)皮带传动
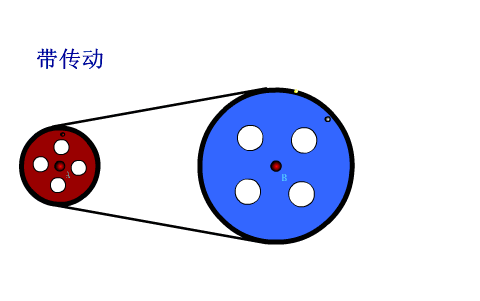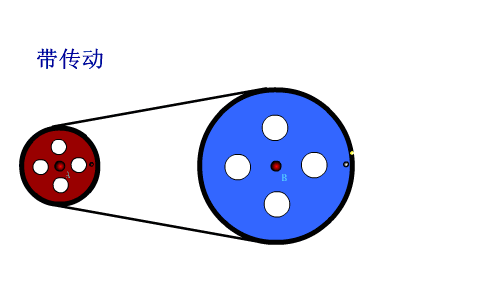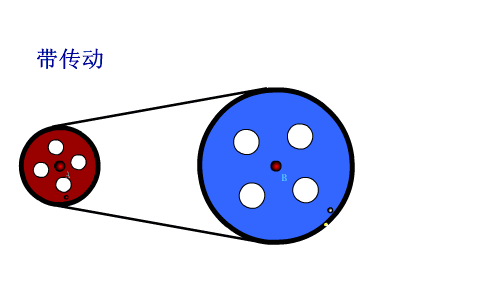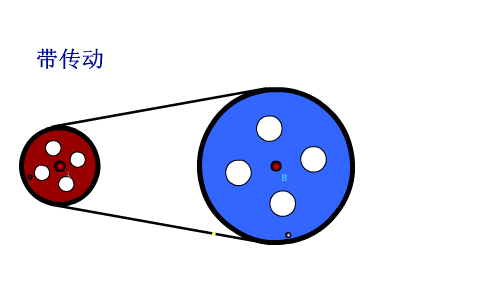

观察动画,小轮边缘和皮带接触,如果皮带不打滑,则小轮边缘的线速度大小和皮带的速度大小相等,同理大轮边缘的点的线速度大小也和皮带运动的速度大小相等,所以AC两点的线速度大小相等。AC两点的角速度和半径成反比,小轮半径小,角速度大,转的更快。
(二)同轴传动

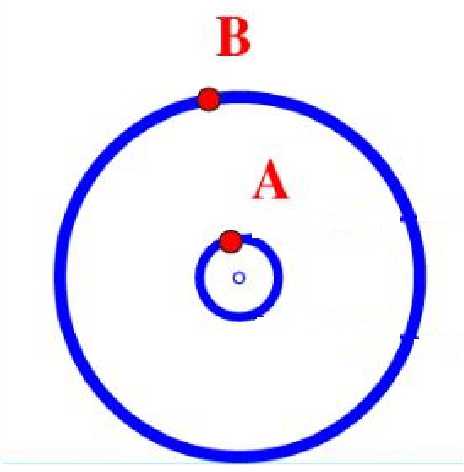
AB两点相等时间转过的角度相等,所以角速度相等,线速度和半径成正比。B点做圆周运动的半径大,线速度也要大。
生活当中很多地方都用到了传动模型。
思考讨论:以下模型分别属于哪一类传动模型?

1、齿轮传动:轮子边缘线速度大小相等。
2、摩擦传动:轮子边缘线速度大小相等。
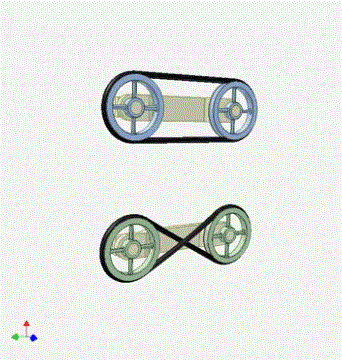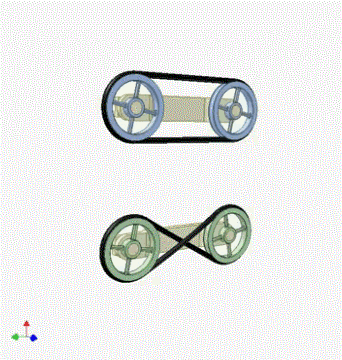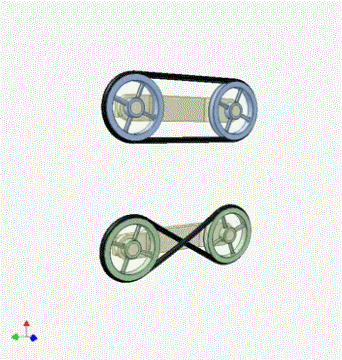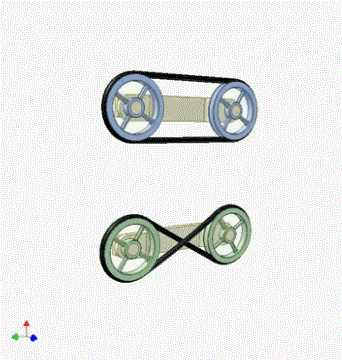
3、皮带传动:轮子边缘线速度大小相等。

4、地球模型属于同轴传动模型。
现在我们已经知道传动模型的特点了,那我们回到最初的问题,ABC三点线速度和角速度到底有什么关系呢?
例题巩固:图中所示为自行车传动装置,右轮的半径为2r,C是它边缘上的一点。左侧大轮的半径为4r,小轮的半径为r,A点和B点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑。则ABC三点线速度之比为__________,ABC三点角速度之比为___________。
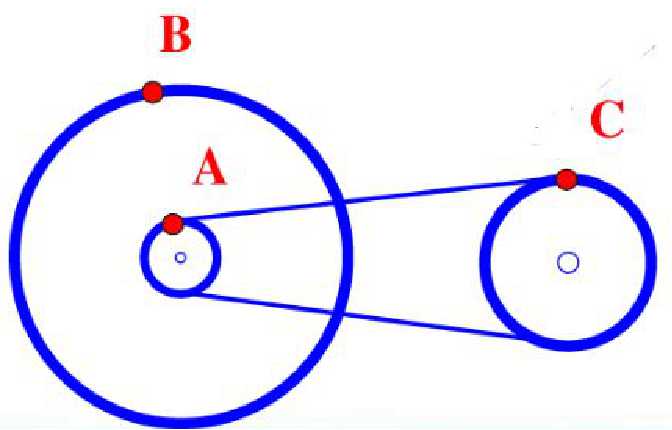
学生完成。
根据例题总结解决这类问题的解题步骤是怎样的?
确定研究点,确定模型,确定线速度、角速度关系。
1:自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,如图所示.在自行车正常骑行时,下列说法正确的是( )
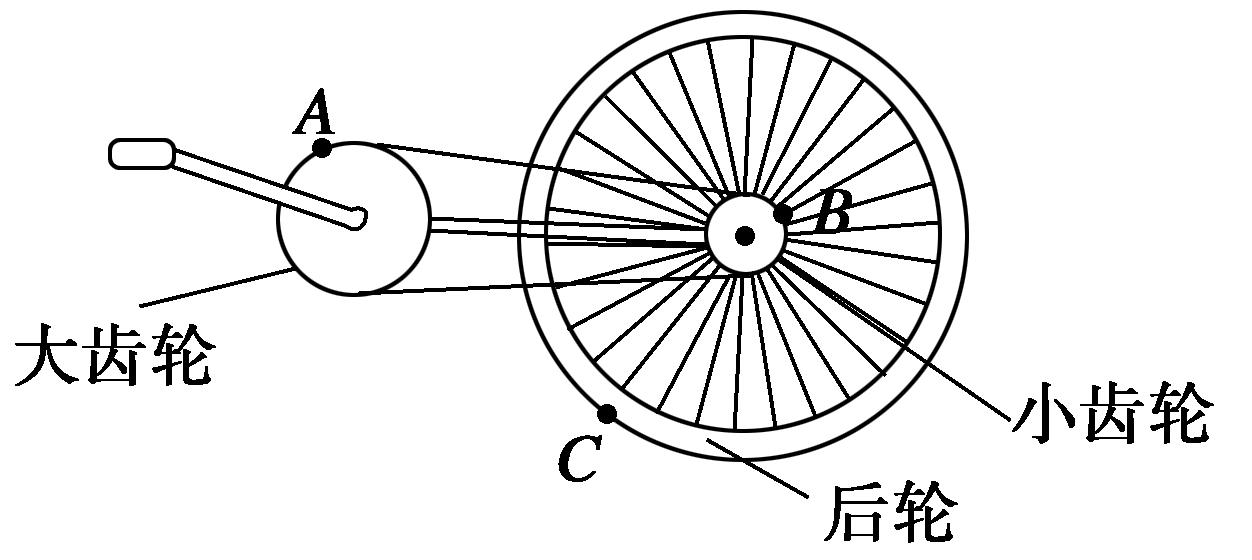
A.A、B两点的线速度大小相等
B.B、C两点的角速度大小相等
C.A、B两点的角速度与其半径成反比
D.A、B两点的角速度与其半径成正比
2:如图所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3.若甲轮的角速度为ω1,则丙轮的角速度为( )
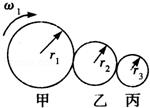
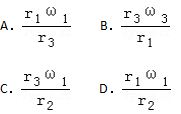
设为正确答案